Линейные однородные системы дифференциальных уравнений

Система дифференциальных уравнений

Существуют два основных типа систем дифференциальных уравнений:

– Линейные однородные системы дифференциальных уравнений

– Линейные неоднородные системы дифференциальных уравнений

И два основных способа решения системы дифференциальных уравнений:

– Метод исключения. Суть метода состоит в том, что в ходе решения система ДУ сводится к одному дифференциальному уравнению.

– С помощью характеристического уравнения (так называемый метод Эйлера).

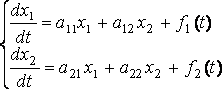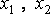где - искомые функции от t; 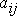- постоянные числа;

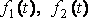- заданные функции, называется системой линейных дифференциальных уравнений с постоянными коэффициентами второго порядка.

Такую систему методом исключения можно привести к одному линейному урав-нению не выше второго порядка.

Линейные однородные системы дифференциальных уравнений

Простейшая однородная система дифференциальных уравнений имеет следующий вид: 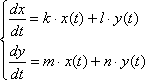, где 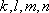– это числа (числовые коэффициенты). Самые обычные числа. В частности, один, несколько или даже все коэффициенты могут быть нулевыми, но такое встречается редко, поэтому числа 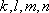чаще всего не равны нулю.

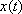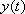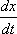и – это неизвестные функции. В качестве независимой переменной выступает переменная – это «как бы икс в обычном дифференциальном уравнении».

и 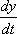– первые производные неизвестных функци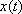й и 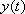соответственно.

Решить систему дифференциальных уравнений это значит, найти такие функци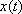и и 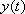, которые удовлетворяют и первому и второму уравнению системы. Как видите, принцип очень похож на обычные системы линейных уравнений. Только там корнями являются числа, а здесь – функции.

Найденный ответ записывают в виде общего решения системы дифференциальных уравнений: 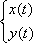Для системы ДУ можно решить задачу Коши, то есть, найти частное решение системы, удовлетворяющее заданным начальным условиям. Частное решение системы тоже записывают с фигурными скобками.

Более компактно систему можно переписать так: 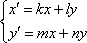. Но в ходу традиционно более распространен вариант решения с производными, расписанными в дифференциалах, поэтому

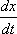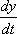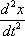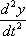и – производные первого порядка; и – производные второго порядка.

Решение системы методом исключения. Суть метода – свести систему к одному дифференциальному уравнению.

Для этого надо взять первое или второе уравнение системы и выражаем из него x или y:

2)Дифференцировать по t обе части (правую и левую) полученного уравнения

Продифференцировав подставим (x и 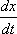) или (y и 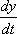) в первое уравнение системы.

Далее провести максимальные упрощения: Получится однородное или неоднородное ДУ.

Если однородное, то составим и решим характеристическое уравнение:

4)Идём за функцие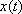й или 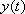, для этого берём уже найденную функцию 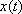или 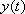, и находим её производную. Дифференцируем по :

Подставим 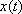или 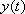и x’(t) или y’(t) в уравнение, которое выражали в самом начале через x или y.

5)Обе функции найдены, запишем общее решение системы: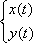

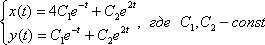
6) Найдем частное решение, соответствующее начальным условиям, если они присутствовали в условии.