Условия реализации программы дисциплины МАТЕМАТИКА

Требования к минимальному материально-техническому обеспечению

Реализация программы дисциплины требует наличия учебного кабинета «Математика»;

Оборудование учебного кабинета:

1. Рабочее место преподавателя.

2. Рабочие места для обучающихся.

3. Комплект плакатов (стендов) для оформления кабинета

4. Комплект схем, таблиц для демонстраций.

5. Комплект учебно-методической документации.

6. Учебные наглядные пособия и презентации по дисциплине (диски, плакаты).

7. Задания для практических и самостоятельных работ, методические указания по их выполнению и образцы выполненных работ.

8. Учебно-методическая литература.

9. Электронные учебники.

Технические средства обучения:

1. Демонстрационный (мультимедийный) комплекс;

Информационное обеспечение обучения

Перечень рекомендуемых учебных изданий, Интернет-ресурсов, дополнительной литературы

Основные источники:

1. Федеральный государственный образовательный стандарт среднего профессионального образования.

2. Мордкович А.Г. Алгебра и начала анализа. 10 – 11 классы. В 2 ч. Ч.1. Учебник для общеобразовательных учреждений - М.: Мнемозина, 2007.

3. Мордкович А.Г. Алгебра и начала анализа. 10 – 11 классы. В 2 ч. Ч.2. Задачник для общеобразовательных учреждений - М.: Мнемозина, 2007.

4. Смирнова И.М. Геометрия. 10 - 11 классы: учеб. для учащихся общеобразоват. учреждений (базовый уровень) – М. : Мнемозина, 2010.

Дополнительные источники:

1. Змеева Е.Е., Гриншпон И.Э. Элементы комбинаторики, теории вероятностей, статистики. - Томск: ТОИПКРО, 2005.

2. Башмаков М.И. Алгебра и начала математического анализа (базовый уровень). 10 кл. – М., 2005.

3. Башмаков М.И. Алгебра и начала математического анализа (базовый уровень). 11 кл. – М., 2005.

4. Башмаков М.И. Математика (базовый уровень). 10—11 кл. – М., 2005.

5. Башмаков М.И. Математика: 10 кл. Сборник задач: учеб. пособие. – М., 2004.

6. Башмаков М.И. Математика: учебник для 10 кл. – М., 2004.

7. Дорофеев Г.В. Сборника заданий для подготовки и проведение письменного экзамена по математике (курс А) и алгебре и началам анализа (курс В) за курс средней школы. 11 класс.- М.: Дрофа, 2006.

8. Тригонометрия. Учебник для 10 кл./ Ю.Н. Макарычев, Н.Т. Миндюк, С.Н. Нешков, С.Б. Суворова. – МL: Просвещение,2001.

9. Мордкович А.Г., Тульчинская Е.Е. Алгебра и начала анализа. 10 – 11 классы: Контрольные работы для общеобразоват. учрежд. – М.: Мнемозина, 2000.

10. Погорелов А.В. Геометрия: Учеб. для 10-11 кл. общеобразоват. учреждений. – М.: Просвещение, 2000.

11. www.festival.1september.ru

12. www.bymath.net

13. http://geometry2006.narod.ru

14. http://softtutograf.com/

4. Контроль и оценка результатов освоения дисциплины МАТЕМАТИКА

Контроль и оценка результатов освоения дисциплины осуществляется преподавателем в процессе проведения практических занятий, контрольных работ, а также выполнения обучающимися индивидуальных заданий.

Результаты обучения	Формы и методы контроля и оценки результатов обучения
освоенные умения:
Выполнение арифметических действий над числами, сочетая устные и письменные приемы; нахождение приближенных значений величин и погрешности вычислений (абсолютная и относительная); сравнивание числовых выражений.	Оценка результатов практических работ. Оценка результатов самостоятельных работ по нахождению и использованию математической информации по заданной тематике.
Нахождение значения корня, степени, логарифма, тригонометрических выражений на основе определения, используя при необходимости инструментальные средства; умение пользоваться приближенной оценкой при практических расчетах.
Выполнение преобразования выражений, применяя формулы, связанные со свойствами степеней, логарифмов, тригонометрических функций.
Вычисление значения функции по заданному значению аргумента при различных способах задания функции.	Оценка результатов практических работ. Оценка результатов самостоятельных работ по нахождению и использованию математической информации по заданной тематике.
Определение основных свойств числовых функций, иллюстрирование их на графиках.
Построение графиков изученных функций, иллюстрирование по графику свойства элементарных функций.
Использование понятия функции для описания и анализа зависимостей величин.
Нахождение производных элементарных функций.	Оценка результатов практических работ. Оценка результатов самостоятельных работ по нахождению и использованию математической информации по заданной тематике.
Использование производной для изучения свойств функций и построения графиков.
Применение производной для проведения приближенных вычислений, решение задач прикладного характера на нахождение наибольшего и наименьшего значения.
Вычисление в простейших случаях площадей и объемов с использованием определенного интеграла.	Оценка результатов практических работ. Оценка результатов самостоятельных работ по нахождению и использованию математической информации по заданной тематике.
Решение рациональных, показательных, логарифмических, тригонометрических уравнений, сводящихся к линейным и квадратным, а также к аналогичным неравенствам и системам. Использование графического метода решения уравнений и неравенств.	Оценка результатов практических работ. Оценка результатов самостоятельных работ по нахождению и использованию математической информации по заданной тематике.
Изображение на координатной плоскости решения уравнений, неравенств и систем с двумя неизвестными. Составление и решение уравнений и неравенств, связывающих неизвестные величины в текстовых (в том числе прикладных) задачах.
Решение простейших комбинаторных задач методом перебора, а также с использованием известных формул. Вычисление в простейших случаях вероятности событий на основе подсчета числа исходов.	Оценка результатов практических работ. Оценка результатов самостоятельных работ по нахождению и использованию математической информации по заданной тематике.
Распознавание на чертежах и моделях пространственных форм; соотношение трехмерных объектов с их описаниями, изображениями.	Оценка результатов практических работ. Оценка результатов самостоятельных работ по нахождению и использованию математической информации по заданной тематике.
Описание взаимного расположения прямых и плоскостей в пространстве, аргументирование своих суждений об этом расположении. Анализирование в простейших случаях взаимного расположение объектов в пространстве. Изображение основных многогранников и круглых тел; выполнение чертежей по условиям задач. Построение простейших сечений куба, призмы, пирамиды.
Решение планиметрических и простейших стереометрических задач на нахождение геометрических величин (длин, углов, площадей, объемов). Использование при решении стереометрических задач планиметрических фактов и методов. Проведение доказательных рассуждений в ходе решения задач.
усвоенные знания:
Значение математической науки для решения задач, возникающих в теории и практике; широту и в то же время ограниченность применения математических методов к анализу и исследованию процессов и явлений в природе и обществе	Оценка результатов практических работ Оценка результатов выполнения индивидуальных заданий Оценка результатов контрольных работ на знание решения прикладных задач в области профессиональной деятельности Оценка результатов экзамена
Значение практики и вопросов, возникающих в самой математике для формирования и развития математической науки; историю развития понятия числа, создания математического анализа, возникновения и развития геометрии
Универсальный характер законов логики математических рассуждений, их применимость во всех областях человеческой деятельности
Вероятностный характер различных процессов окружающего мира

ПРИЛОЖЕНИЯ

Приложение 1

Контрольная работа № 1

Вариант 1

1. Переведите из радианной меры в градусную .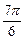

2. Упростите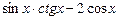

3. Постройте график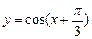

4. Решите уравнения

А)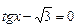

Б)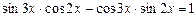

5. Вычислите tgx, если sinx = 0,6 и 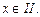четв.

6. Решите уравнение: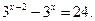

7. Решите уравнение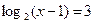

8. Решите уравнение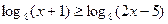

9. Для функции 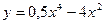найдите:

a) промежутки возрастания и убывания функции;

b) точки экстремума;

c) наибольшее и наименьшее значения функции на отрезке .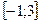

10. Составьте уравнение касательной к графику функции 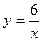в точке х₀ = 3.

11. Площадь прямоугольного участка 121 м². При каких размерах участка длина окружающего его забора будет наименьшей?

Вариант 2

1. Переведите из градусной меры в радианную .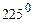

2. Упростите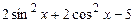

3. Постройте график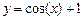

4. Решите уравнения

А)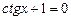

Б)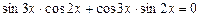

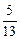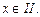5. Вычислите tgx, если sinx = и четв.

6. Решите уравнение: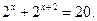

7. Решите уравнение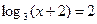

8. Решите уравнение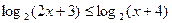

9. Для функции 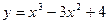найдите:

a) промежутки возрастания и убывания функции;

b) точки экстремума;

c) наибольшее и наименьшее значения функции на отрезке .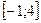

10. Составьте уравнение касательной к графику функции 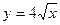в точке

х₀ = 4.

11. Площадь прямоугольного участка 144 м². При каких размерах участка длина окружающего его забора будет наименьшей?

Приложение 2

Контрольная работа № 2

1. Найти вероятность того, что при бросании двух игральных костей выпадет от m₁ до m₂ очков.

№ варианта
m1
m2

2. Среди n лотерейных билетов m выигрышных. Наудачу вынимают 2 билета. Найти вероятность того, что:

а) среди них нет выигрышных;

б) среди них хотя бы один выигрышный;

в) оба билета выигрышные.

№ варианта
n
m

3. (1 вариант) На склад поступило 2 партии изделий: первая - 2000 штук, вторая - 3000 штук. Средний процент нестандартных изделий в первой партии 2%, во второй - 5%. Найти вероятность того, что наудачу взятое со склада изделие будет нестандартным.

4. (2 вариант) На склад поступило 3 партии изделий: первая - 1000 штук, вторая - 3000 штук, третья - 2000 штук. Средний процент нестандартных изделий в первой партии 15%, во второй - 10%., в третьей - 5% Наудачу взятое со склада изделие оказалось нестандартным. Найти вероятность того, что оно из второй партии

5. (1 вариант) Два курсанта одновременно стреляют в цель, один из них попадает. Вероятность попадания первым курсантом - 0.4, вторым - 0.6. Найти вероятность того, что первый курсант промахнулся.

6. (2 вариант) Два курсанта одновременно стреляют в цель, один из них попадает. Вероятность попадания первым курсантом - 0.3, вторым - 0.5. Найти вероятность того, что второй курсант промахнулся.

Приложение 3

Контрольная работа № 3

Вариант 1

1. Через конец А отрезка АВ проведена плоскость. Через конец В и точку С этого отрезка проведены параллельные прямые, пересекающие плоскость в точках В₁ и С₁. Найдите длину ВВ₁, если СС₁ = 16м, АС: ВС = 4:5 .

2.Прямые АВ, АС и АD попарно перпендикулярны.

Найти отрезок СD, если АВ = 6 см, ВС = 9 см, АD = 1 см.

3. Из точек А и В, лежащих в двух перпендикулярных плоскостях, опущены перпендикуляры АС и BD на прямую пересечения плоскостей. Найти длину отрезка АВ, если АС = 5, BD = 2 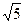, СD = 6.

4. Расстояния от точки А до вершин квадрата равны 5 см. Найти расстояние от точки А до плоскости квадрата, если сторона квадрата равна 2 см.

5. Концы отрезка АВ, непересекающего плоскость, удалены на расстоянии 2,4 см, 7,6 см. Найдите расстояние от середины М отрезка АВ до этой плоскости.

6. Цилиндр образован вращением прямоугольника с диагональю 5 см вокруг стороны длиной 3 см. Найдите объём цилиндра и площадь его полной поверхности.

7. Сторона основания правильной треугольной пирамиды 6 см, боковое ребро 10 см. Найдите площадь полной поверхности пирамиды.

Вариант 2

1. Через конец B отрезка BD проведена плоскость. Через конец D и точку M этого отрезка проведены параллельные прямые, пересекающие плоскость в точках D₁ и M₁. Найдите длину DD₁, если СС₁ = 10м, DM: MN = 3:5 .

2. Прямые АВ, АС и АD попарно перпендикулярны.

Найти отрезок СD, если АВ = 2 см, ВС = 13 см, АD = 3 см.

3. Из точек А и В, лежащих в двух перпендикулярных плоскостях, опущены перпендикуляры АС и BD на прямую пересечения плоскостей. Найти длину отрезка АВ, если АD = 10, BD = 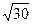, СD = 3.

4. Расстояния от точки А до вершин квадрата равны 6 см. Найти расстояние от точки А до плоскости квадрата, если сторона квадрата равна 4 см.

5. Точка А лежит в плоскости, точка В – на расстоянии 12,5 см, от этой плоскости. Найдите расстояние от точки М до плоскости, которая делит отрезок АВ в отношении АМ:МВ = 2 : 3.

6. Прямоугольный треугольник с гипотенузой 13 см вращается вокруг оси, содержащей катет длиной 5 см. Найдите объём полученного конуса и площадь его полной поверхности.

7. Сторона основания правильной треугольной пирамиды 6 см, боковое ребро 10 см. Найдите объём пирамиды.