Подбор поперечного сечения по нормальным напряжениям
Кафедра механики
Расчетно-графическая работа №2
По дисциплине: Прикладная механика
(наименование учебной дисциплины согласно учебному плану)
Тема: Построение эпюр перерезывающих сил, изгибающих моментов и выборов сечений балок.
Выполнил: студент гр. РТ-07 ______________ /Тонаганян А.В./
(подпись) (Ф.И.О.)
ПРОВЕРИЛ: доцент ____________ /Монахов В.Н./
(подпись) (Ф.И.О.)
Санкт-Петербург
Задание:
Построить эпюры перерезывающих сил, изгибающих моментов и подобрать сечения балок.
Задача 1
Исходные данные.
 | P |  |  |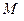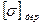
| кН/м | кН | кНм | МПа |
| 5 | 15 | 25 | 10 |
 | |||||
 | |||||
 | |||||
 | |||||
 | |||||
 | |||||
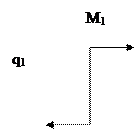3 4 2
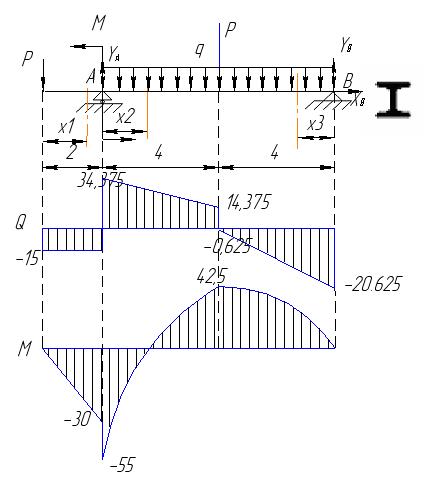
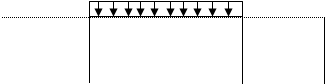
Для данной задачи вычислять реакции не нужно. Если рассечь балку в любом сечении и рассматривать часть балки между сечением и свободным концом, то в выражения для Q и M войдут только приложенные к балке известные нагрузки.
На первом участке x1 изменяется в пределах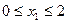 
. Перерезывающая сила на первом участке постоянна: 
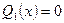. Изгибающий момент на этом участке постоянен 
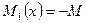, где 
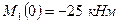и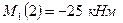 
.
На втором участке x2 изменяется в пределах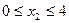 
. Перерезывающая сила на этом участке изменятся линейно: 
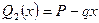, где 
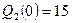и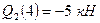 
Изгибающий момент на этом участке изменяется по параболе: 
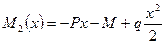; где 
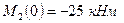и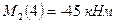 
.
Эпюра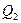 
пересекает ось Х, меняя знак с «-» на «+» слева на право, значит в этой точке будет минимум значения на эпюре М . Найдем значение координаты 
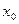, при котором 
.
.
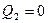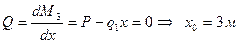Найдем минимальное значение изгибающего момента
.
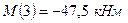На третьем участке x3 изменяется в пределах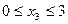 
. Перерезывающая сила на третьем участке постоянна: 
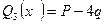. Изгибающий момент на этом участке изменяется линейно: 
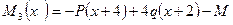; где 
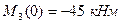и 
.
Подбор поперечного сечения по нормальным напряжениям
Абсолютная величина максимального изгибающего момента равна 47,5 кНм. Тогданеобходимый момент сопротивления
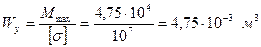
Момент сопротивления круглого поперечного сечения относительно центральной оси равен 
= 
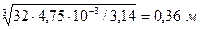
Задача 2
Исходные данные.
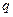 1 | 2 | M |  |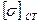
| кН/м | кН/м | кНм | МПа |
| 5 | 10 | 25 | 160 |
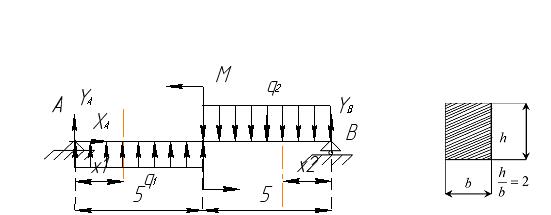
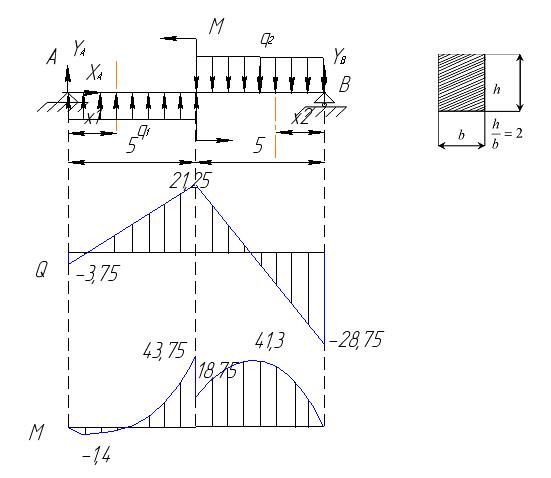
Для определения Q и M в любом сечении балки необходимо знать все внешние силы, действующие на балку, т.е. приложенные нагрузки и опорные реакции.
Определим неизвестные реакции опор, используя уравнения равновесия статики.
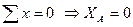
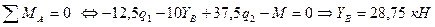
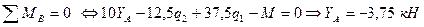
Для проверки составим уравнение статики, не использованное при расчете реакций, например, сумму проекций всех сил на ось Y:
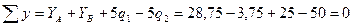
На первом участке x1 изменяется в пределах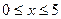 
. Перерезывающая сила на первом участке изменяется линейно: 
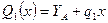, где 
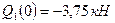и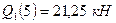 
. Изгибающий момент на этом участке изменяется по параболе: 
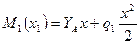, где 
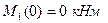и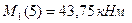 
.
Эпюра 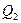пересекает ось Х, меняя знак с «-» на «+» слева на право, значит в этой точке будет минимум значения на эпюре М . Найдем значение координаты 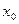, при котором .
.
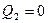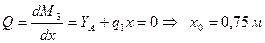Найдем минимальное значение изгибающего момента
.
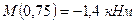На втором участке x2 изменяется в пределах 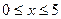. Перерезывающая сила на втором участке изменяется линейно: 
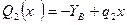где 
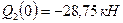и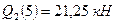 
. Изгибающий момент на этом участке изменяется по параболе: 
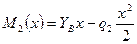; где 
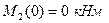и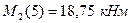 
.
Эпюра 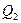пересекает ось Х, меняя знак с «+» на «-» слева на право, значит в этой точке будет максимум значения на эпюре М . Найдем значение координаты 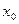, при котором .
.
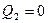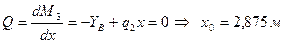Найдем максимальное значение изгибающего момента
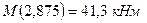
Подбор поперечного сечения по нормальным напряжениям
Абсолютная величина максимального изгибающего момента равна 43,75 кНм. Тогданеобходимый момент сопротивления
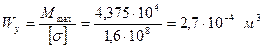
Момент сопротивления прямоугольника относительно нейтральной оси равен
.
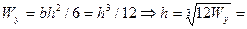
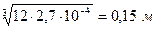
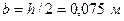
Задача 3
Исходные данные
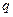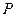| |  | M | |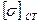
| кН/м | кН | кНм | МПа |
| 5 | 15 | 25 | 160 |
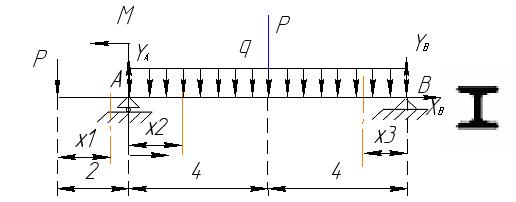
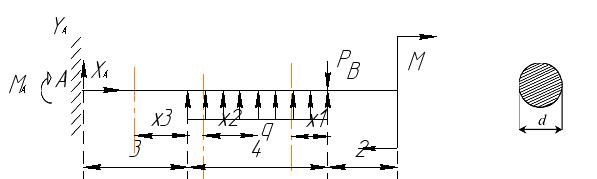
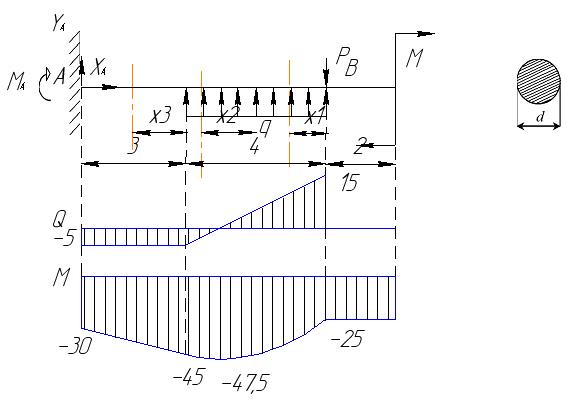
Для определения Q и M в любом сечении балки необходимо знать все внешние силы, действующие на балку, т.е. приложенные нагрузки и опорные реакции.
Определим неизвестные реакции опор, используя уравнения равновесия статики.
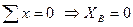
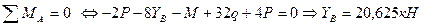
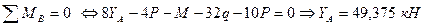
Для проверки составим уравнение статики, не использованное при расчете реакций, например, сумму проекций всех сил на ось Y:
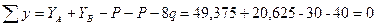
На первом участке x1 изменяется в пределах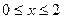 
. Перерезывающая сила на первом участке постоянна: 
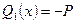. Изгибающий момент на этом участке изменяется линейно: 
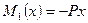; где 
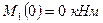и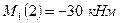 
.
На втором участке x2 изменяется в пределах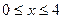 
. Перерезывающая сила на втором участке изменяется линейно: 
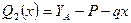, где 
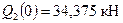и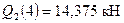 
. Изгибающий момент на этом участке изменяется по параболе: 
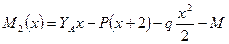; где 
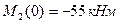и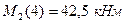 
.
На третьем участке x3 изменяется в пределах 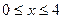. Перерезывающая сила на третьем участке изменяется линейно: 
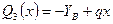, где 
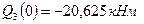и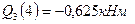 
. Изгибающий момент на этом участке изменяется по параболе: 
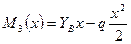; где 
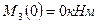и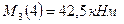 
.
