Построение регрессионных моделей

Лабораторная работа 1

Тема: «Планирование экстремальных экспериментов. Построение регрессионных моделей»

Цель работы:изучение основных понятий, определений, принципов теории планирования экспериментов, приобретение навыков проведения экспериментов по построению математических моделей, ознакомление с методикой построения регрессионных моделей.

Основные понятия

Эксперимент – метод научного исследования, когда исследователь активно и целенаправленно воздействует на объект исследования путем создания искусственных условий или использования естественных условий, необходимых для выявления конкретных свойств объекта.

Эксперименты делятся на пассивные и активные (управляемые). В пассивном эксперименте контролируемые (входные) параметры нельзя изменять, в активном – можно.

Планирование эксперимента – область знания, связанная с построением и оптимизацией математических моделей.

Объект исследования рассматривается как носитель некоторых неизвестных или подлежащих исследованию свойств и качеств – своеобразный «черный ящик». При этом вектор 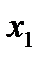, 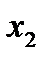… 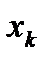представляет собой группу контролируемых и управляемых величин, которые могут изменяться определенным образом в ходе эксперимента, а 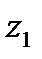, 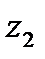… 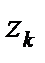контролируемые характеристики. Характеристики ( 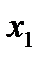, 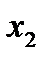… 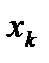) также называют факторами или управляемыми воздействиями. Функция Y – функция отклика (поверхность отклика), представляет собой реакцию системы на воздействие факторов.

Также можно выделить и третью, не обозначенную на идеальной модели систему входных сигналов – это шумы или помехи, которые обусловлены многими факторами: ошибками обслуживающего персонала, влиянием внешней среды, погрешностью приборов и т.д. К этой же группе относятся воздействия, которые не могут контролироваться либо из-за их сложности, либо из-за незнания их природы и невозможности контроля.

Характеристики объектов имеют различную физическую природу, а, следовательно, и размерность, что затрудняет построения модели. Поэтому на практике значения факторов, которые имеют реальный физический смысл, нормируют (приводят к определенному ранее заданному набору значений).

Для любого фактора Х существует нижний Хmin и верхний Xmax уровни

изменения значений.

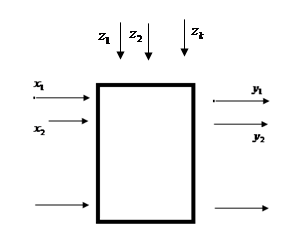
Структурная схема объекта (процесса)

При проведении активного эксперимента

Факторное пространство

Приведем алгоритм нормировки фактора:

· выбираем масштаб и положение осей координат таким образом, чтобы 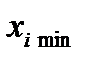соответствовало –1, а 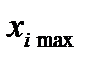+1.

· вычисляем значение 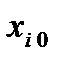для данного фактора следующим образом .

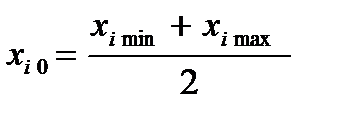· вычисляем интервал изменения фактора .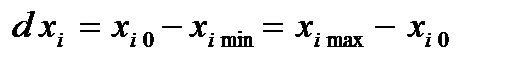

· находим нормированное значение 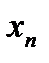для каждого фактора .

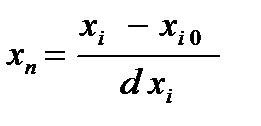Зависимость реакции объекта от точки факторного пространства называется функцией отклика 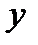, а ее геометрическое представление 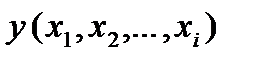– поверхностью отклика. Векторов значений функции отклика может быть столько, сколько опытов.

Проведение эксперимента

Эксперимент состоит из опытов (воспроизведение исследуемого явления). Под планированием эксперимента понимают выбор плана эксперимента – совокупности данных, определяющих число, условия и порядок реализации опытов. Каждый опыт эксперимента характеризуется определенным набором значений факторов.

Вектор, содержащий некоторый набор конкретных значений факторов 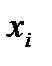, определяет q-ю точку плана эксперимента. Совокупность векторов 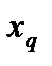(q = 1, 2, …, n) образует план эксперимента (матрица, содержащая k строк и n столбцов, каждая строка которой образует точку плана эксперимента, а столбец фактор эксперимента).

			…
			…
…	…	…	…	…
			…

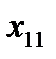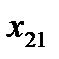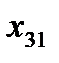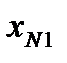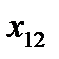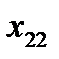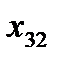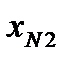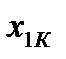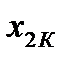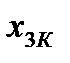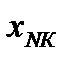Совокупность всех точек плана, отличающихся уровнем хотя бы одного

фактора (различных строк матрицы планирования), называется спектром плана. Матрица, получаемая из всех различных строк плана – матрица спектра плана. Она отличается от приведенной выше матрицы только числом строк (из-за отсутствия повторяющихся точек плана). При количестве точек спектра плана G, ее размерность будет составлять: G строк на N столбцов.

Применяется также матрица дублирования, размерность которой совпадает с размерностью матрицы спектра плана. Она имеет вид:

			…
			…
…	…	…	…	…
			…

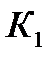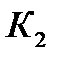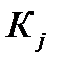Здесь 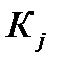- число параллельных опытов в точке спектра плана с номером j (j = 1, 2, …, N). Т.е. это число характеризует дублирование соответствующей строки в матрице спектра плана.

Построение регрессионных моделей

Для описания объектов управления часто используются полиномиальные модели. При этом в качестве базисного выражения используется ряд Тейлора, имеющий конечное число членов.

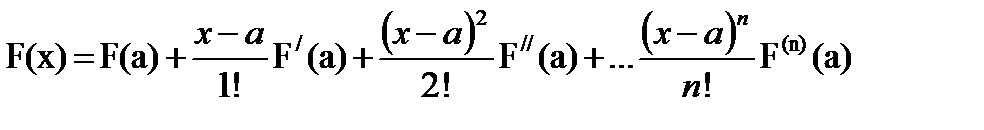
Но при использовании аппроксимирующего полинома Тейлора в приведенном выше виде возникает ряд проблем, связанных с нахождением производных, так как неизвестна функция, а известен только ряд ее значений.

Поэтому заменим полином Тейлора на аналогичное ему уравнение регрессии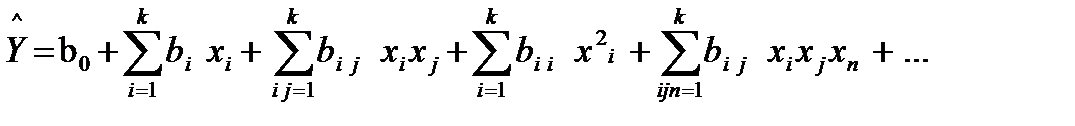

где k – число столбцов в матрице планирования. Построим линейную регрессионную модель. Для ее экспериментального получения используем план первого порядка (факторный эксперимент первого порядка).

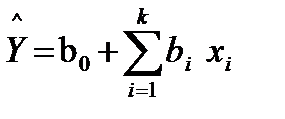
Для k-факторного эксперимента достаточно k+1 опытов. При определении коэффициентов регрессии должны выполняться необходимые и достаточные условия:

1. Результаты измерений выходной величины Y в N точках факторного пространства – нормально распределенные величины.

2. Дисперсии реализации во всех точках факторного пространства одинаковы, то есть не зависят от абсолютного значения величины и от направления обхода факторного пространства.

3. Входные переменные (факторы) – это независимые величины, которые измеряются с бесконечно малой ошибкой по отношению к ошибке выходной величины.

Оценка выполняется по критерию Фишера.

Любой многофакторный эксперимент является результатом варьирования всех факторов.