Розміру «вікна шифрування» і Вернама

1. Опис методів шифрування

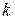1.1. Шифр на основі поворотної решітки (XVI вік). Ідея поворотної решітки як засобу шифрування належить італійському математику Д. Кардано. Така решітка – це квадрат розміру (в якості значення обирається парне число, хоча це – необов’язкова вимога), в якому так вирізані квадратики розміру , що при поворотах решітки на кут кожна клітка квадрату розміру виявлялася під вирізом не більше одного разу. Для того, щоб забезпечити однозначність процесу перетворення інформації один з боків поворотної решітки позначався. Вихідним положенням решітки вважалось таке, при якому позначений бік мав фіксоване розташування (наприклад, внизу). Шифрування здійснювалось в такий спосіб. Решітка накладалася у вихідному положенні на аркуш паперу. В вирізи послідовно, літера за літерою, вписувалась інформація, яку необхідно передати адресату. Після заповнення всіх вирізів, решітка поверталася на кут (для забезпечення однозначності процесу перетворення інформації напрям повороту заздалегідь обговорювався відправником і адресатом) і описана процедура повторювалась. Після 3-х поворотів решітка знімалася і незаповнені позиції (якщо такі були) квадрату розміру заповнювались довільними символами алфавіту, який використовувався. Якщо місця для запису інформації не вистачало, то решітка накладалася на нове місце аркушу (поруч або нижче), і описана вище процедура повторювалась. Якщо при заповненні останнього квадрату розміру вся інформація виявлялась записаною, але не всі вирізи в решітці були повністю використані, то в вільні позиції записувалась заздалегідь обговорена послідовність символів алфавіту. Така послідовність грає роль фінального маркера, що фіксує закінчення інформаційної послідовності. Отриманий шифротекст відправлявся адресату. Адресат, що мав трафарет, повторював всі дії відправника з тією різницею, що замість «запису» інформації здійснював її «зчитування».

Приклад 2.1. В якості засобу шифрування обрана поворотна решітка розміру 4×4, зображена на рис. 3.1.а. В якості фінального маркера з послідовності АБВГДЕЖЗИЙКЛМНО, обирається початковий відрізок, що має довжину, необхідну для заповнення всіх вирізів, які не були використані. На рис. 3.1.б наведений шифротекст фрази:

МАТЕМАТИКА_–_ЭТО_“ГИМНАСТИКА”_УМА!

Рисунок 2.1. Шифр на основі поворотної решітки: а) поворотна решітка розміру

4×4 (вирізані квадратики − заштриховані клітки); б) шифротекст.

Поворотна решітка розміру – повна, якщо після обробки за її допомогою квадрату розміру відсутні незаповнені позиції, якщо 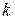– парне число і є в точності одна незаповнена позиція, що розташована в центрі квадрату, якщо 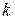– непарне число.

Теорема 2.1. Кількість повних поворотних решіток розміру дорівнює

. (2.1)

Доведення. Зафіксуємо число . Розіб’ємо множину всіх кліток квадрату розміру на блоків так, що будь-який блок переходить на себе при повороті квадрату на кут . Знайдемо значення :

;

.

Повна поворотна решітка розміру характеризується тим, що:

1) в кожному 4-х елементному блоці вирізається в точності одна клітка;

2) якщо 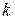– непарне число, то не вирізається клітка, що належить одноелементному блоку .

Кількість способів вибору клітки, що вирізається у фіксованому блоці дорівнює 4. А оскільки вибір кліток, що вирізаються, в різних блоках здійснюється незалежно, то

,

,

звідки і витікає дійсність рівності (2.1).

Теорема доведена.

1.2. Шифр Ардженті (XVII вік). Заснований на таблиці Ардженті. В ній вперше були вдало сполучені наступні три ідеї:

1) для символів вихідного алфавіту, які найчастіше зустрічаються, використовувалось декілька шифр-позначень (що робило частотний аналіз шифротексту практично нездійсненим);

2) використовувались шифр-позначення різної довжини;

3) шифр-позначення застосовувались для сполучень літер, складів і цілих фраз, які часто зустрічались.

В результаті реалізації останньої ідеї «алфавіт» , що нумерував стовпці таблиці Ардженті, містив близько 1200 символів.

Шифрування здійснювалось за допомогою послідовної заміни кожного символу повідомлення будь-яким його шифр-позначенням. Такий підхід приводить до неоднозначності шифрування, оскільки для одного і того ж повідомлення можуть бути отримані різні шифротексти, причому різної довжини. Однак така неоднозначність не впливає ні на коректність, ні на складність процесу розшифровки. Адресат послідовно проглядав шифротекст, здійснюючи пошук чергового фрагменту в стовпцях таблиці Ардженті. Виявивши такий фрагмент, він замінював його символом , який нумерує цей стовпець.

Приклад 2.2. Таблиця 2.1 – це варіант таблиці Ардженті для російської мови.

Таблиця 2.1 (початок)

Таблиця 2.1 (закінчення)

Скористаємося цією таблицею і зашифруємо двома способами фразу:

МАТЕМАТИКА_–_ЭТО_“ГИМНАСТИКА”_УМА!

Спосіб 1. Послідовно шифруємо кожний символ. Отримаємо шифр текст:

Спосіб 2. Здійснимо шифрування, вважаючи символами алфавіту сполучення літер МАТ, МА, ТИ і КА. Отримаємо шифротекст:

5059952574495956816888912727904679244371744926148452594.

1.3. Шифр з варіацією розміру «вікна» шифрування (XVII вік). Очевидно, О. Рішел’є (XVII вік) вперше застосував шифр, для якого довжина чергового блоку вихідного тексту, що шифрується, варіювалась заздалегідь запропонованим способом. З цією метою фіксувалась послідовність перестановок , яка грала роль сеансового ключа, де 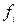– перестановка елементів множини .

Шифрування вихідного повідомлення здійснювалось наступним чином. Вихідний текст розбивався на блоки, довжини яких утворювали початковий відрізок (нескінченої) періодичної послідовності

.

За необхідністю останній блок доповнювався фінальним маркером до потрібної довжини. Шифрування -го блоку вихідного тексту здійснювалось у відповідності до правила:

,

де 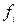– такий елемент сеансового ключа, що . Адресат, що має сеансовий ключ , розбивав шифротекст на блоки, довжини яких утворювали початковий відрізок (нескінченої) періодичної послідовності

.

Розшифровка -го блоку шифротексту здійснювалась наступним чином: обирався такий елемент 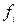сеансового ключа, що і блок замінювався блоком , де

.

Приклад 2.3. Розглянемо наступний варіант шифру О. Рішел’є: в якості сеансового ключа обрана послідовність перестановок:

– перестановка елементів множини ,

– перестановка елементів множини ,

– перестановка елементів множини ,

а в якості фінального маркера з послідовності АБВГДЕЖЗИК… обирається початковий відрізок, що має необхідну довжину.

Зашифруємо за допомогою цього шифру фразу:

МАТЕМАТИКА_–_ЭТО_“ГИМНАСТИКА”_УМА!

Послідовність довжин блоків вихідного тексту має наступний вид:

….

Оскільки довжина повідомлення, що шифрується, дорівнює 34, то доповнимо його відрізком довжини , тобто фінальними маркером АБВГДЕЖЗ. Отримаємо вихідний текст:

МАТЕМАТИКА_–_ЭТО_“ГИМНАСТИКА”_УМА!АБВГДЕЖЗ

Розіб’ємо вихідний текст на блоки, довжини яких дорівнюють . Отримаємо

Оскільки

, , , , , , ,

то

МАТЕМАТ → ЕМАТТМА, НАСТИКА → ТНКСАИА.

Оскільки

, , , , ,

то

ИКА_– → –И_АК, ”_УМА → А”МУ_.

Оскільки

, , , , ,

, , , ,

то

_ЭТО_“ГИМ → Э“М_ГТО_И, !АБВГДЕЖЗ→АДЗГЕБВ!Ж.

Отже, шифротекст має наступний вид:

ЕМАТТМА–И_АКЭ“М_ГТО_ИТНКСАИАА”МУ_АДЗГЕБВ!Ж

1.4. Шифр Вернама (1917р.). Призначений для шифрування телеграфних повідомлень. В ньому вперше реалізовані наступні три принципи:

1) інформація представлена двійковою послідовністю

;

2) сеансовий ключ – заздалегідь задана двійкова послідовність

;

3) сеансовий ключ 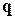представляє собою гамму, тобто «накладається» на інформацію, що генерується, за допомогою порозрядної операції .

Таким чином, для шифру Вернаму шифротекст (див. рис. 4.1.а) має вид

,

де .

Рисунок 2.2 − Шифр Вернама: а) шифрування; б) розшифровка.

Адресат, що має сеансовий ключ, здійснює розшифровку шифротексту через накладення на нього гамми (див. рис. 4.1.б), тобто керуючись правилом

.

Зазначимо наступні дві характеристики шифру Вернама:

1) висока швидкість процесів шифрування/розшифровки інформації легальним користувачем;

2) складність «зламу» шифру повністю визначається складністю ідентифікації гамми.

2. Завдання на проведення лабораторної роботи

2.1. Зашифрувати довільну фразу

1) довжиною не менше 30 символів за допомогою поворотної решітки Кардано ;

2) довжиною не менше 16 символів за допомогою шифру Ардженті.

Решітку Кардано і таблицю Ардженті скласти самостійно.

2.2. Розшифрувати фразу за допомогою решітки Кардано (див. рис. 3.2).

Рисунок 3.2. Поворотна

решітка Кардано

1)_ЭМКНЭТАР_ИЛОЕГСМН_ЕКРИОЧХАЕТЯАШОЯ.РИА_БМННАВАА

2)СЭМЬНПЗАО_ИОИВЛГКАЬЕЛОР_ЧВАМ_ЕМСЯС_БКХВЦГЕИ.ЛДАХ

3)СЭМЬНПЗАО_ИОИВЛГВАЬНЛОЫ_ХВАЕ__НСЖИС._БАСБЛГАУВХО

4)ОЭМЯНСЛАА_ИТС_ОГНИОИЗА_МДБ_ЦИВИКМУИВХ.ГСДТ_АЕЕБС

5)СМН_ЕКЧИАЧХАЕСЯААТККЬЛЛЛАЮ_АЧВ_ВБИРЕАВЖУЗ.ТГАИДУ

6)ИШОУИЕКВВАФ_Н_БРЛОЕССЯЬС_ТУЛВЭОЩСЛРАЕКБИВЧКИЕГ.Т

7)_МНТЕСОИЯЗХОМЛСАО_Л,ИЧ_АКМЗЕПЛК_ЗА,ОВЪВ_,РИЕААМШ

8)ЭАКТ_ЛРЖИЕТЕ_ЧКАЕЕХНСМУ_ТСК_ХРВИВИТВ_.ГОДРРАОЕБО

9)ИТШАОЗТЕАЛК__РБ__ЕЕЕИПКРЛЕ_ЕЗЮРЧБЧЛЕАВЖЬЗ.ТГАИДЕ

10)ИТШАОЗТЕАЛК__РБ_МЕ_ЦИУИКОО_ТМНАВЛНПБУЬВАГНЮ.ЕДА

11)КВММ_ООЕДЙАЙСЕ_РНЛОСИЯЬЕ_Д_ЛИТИСАРОВИ.ГТДО_АРЕБР

12)ВЕС_МКНОНВООЙРОБ_Е_МЫЧЛЕИОЛ_ТОДРЫРБРАВОГТЕ.ОДА_

13)ЛЧЗ_ЕЕИ__КРСОРОЕКОЫОТ_Д_ИТОВОЛХРК_Е.ВТАФБЛ_ОЕВРР

14)РРЕЗЕ_ВКРТФВОАОЛОЩТТАБНООКЛР_,А_О_ДППМУРТУОУГИ__

15)_ВШЛ_РИИЗНМЕЕОААОВМАААВНИОНЛГТФ_.НШГЫАДИЕФЙБРЖВ_

2.3. Зашифрувати довільну фразу довжиною не менше 21 символу за допомогою шифру з варіацією розміру вікна шифрування.

2.4. Зашифрувати довільне слово з 3 літер шифром Вернама.

2.5. Розшифрувати фразу за допомогою шифру з варіацією розміру вікна шифрування. Ключ − послідовність перестановок з прикладу 4.1.

1)_ДБЯСАЛНОТЮЛ_ЙХОКСТОИС_ЕИМТСА_РАХТОВНАЕРКБ

2)ЧКГЮЕ_ЛРНИРЕЕ_ЯЯДТСУЛЖ_ОАГДКОООС_ЩЯВИАЕНББ

3) ДКЙЖ_ЫА_КЧЮЛСЬЕЛЗПОИУ_ТСЯЕВСДГО_ОНЗВАА_РИБ

4)ЛВЧКЕЮ_В_МИСЛАОРВЫ_ОНОВТРНЯЕНЫ_-_ДОЬНСЕЖАТ

5)НД_ИКАЛ_ЛАЧЮЕНЕЕЬ_МНШИ_ЫЛ_НДЩСБООНБДАВИЯЕГ

6) РОТКЫЫТКЙЕТ_ТЛАБА_ОСДИЕБ_ЫЗТОТНЧОТБДАВЬЮСГ

7) ЙСООСКТЕТН_ЬЗС_ИИАВ_ТВОЧ_.ЫТМ_ЗОВЖТАСЕНООЙ

8) СК_АССЛОЛНЖОТ_О-МИ_СНТЖОС_ВЕ_В.ЧЫРЕБЛМОБПА

9) ЕСТЩВСУ7У_ТЕПЛ_БЕРО_МЛ-СКСА_КИСЕЧХДААА_ЗИЧ

10) ДС_ЕНИРАИР_ХЕВКТОНСВ_СЛВС_ОАNP_И_АДЗГЕБВPЖ

11) РЗШ_ЕЕАЗН_ЕИД_ЛИПАЧАОЕАСАЯТГЗ_ИРПВ_Н1М_$_Л

12) АЗАД_ЧАРОБОТННИИСА_АТОТ_ТКМУ(Л_ЯЭЭИ)РДМБКЖ

13) ЧССЙ_АЕАСТИЧТТКЧО,_Ю_СЛ_СРЫАP_N_ИРИЫЛЧАЗ_Н

14)ИОКНЛ_Д_АЫССЛОИНСОЖСТЛ_ЧКАЮВРЮД_ТГБДАВИЕУГ

15) ООАН_ВСКСЙОТС-Е__ТИОНРРШЗИЕАЬМТСОЗЧБАИАД_А

Лабораторна робота №3

Мережа Фей стеля

1. Опис методу шифрування

Мережа Фейстеля.В 1973р. Х. Фейстель (H. Feіstel) запропонував наступний алгоритм перетворення блоку інформації . Нехай – множина ключів. Зафіксуємо відображення . Представимо у вигляді , де , а – операція зчеплення (конкатенації) двійкових послідовностей. -функція – відображення , що визначене для кожного значення ключа рівністю (рис. 3.1). Оскільки , то – бієкція. Для реалізації достатньо на рис. 3.1 поміняти місцями входи і виходи.

Рисунок 3.1. Схема, що реалізує -функцію.

Мережа Фейстеля – будь-яка схема, що реалізує скінченний ітераційний процес, кожен крок (раунд) якого базується на обчисленні -функції, тобто мережа Фейстеля – це послідовне з’єднання схем, зображених на рис. 3.1, можливо забезпечених додатковою логікою.

Приклад 3.1.В якості засобу шифрування обрана 2-раундова мережа Фейстеля. Будемо вважати, що -функції задані таблицею 3.1. Зашифруємо за допомогою мережі літеру «И» з ключами , . Для цього представимо літеру в виді двійкової послідовності: 11001000. Процес і результат шифрування наведено на рис. 3.2. Отже, шифротекст має вид: 00010110.

2. Завдання на проведення лабораторної роботи

2.1. Зашифрувати довільне слово з 3 літер мережею Фейстеля. Ключі обрати самостійно.

2.2. Розшифрувати символ за допомогою мережі Фейстеля. Варіанти завдань і ключі наведені в таблиці 3.2.

Рисунок 3.2. Шифрування мережею Фейстеля

Таблиця 3.1 -функції

аргументи

Таблиця 3.2 − Варіанти завдань

№	шифротекст	ключі
		4,1
		4,1
		4,1
		2,3
		2,3
		2,3
		1,2
		1,2
		1,2
		2,4
		2,4
		3,2
		3,2
		3,2
		4,4
		4,4
		4,4
		1,3
		1,3
		1,3

Лабораторна робота №4

Алгоритм RSA

1. Опис методу шифрування

Асиметрична криптосистема RSA. У 1977 р. вчені МІТ Рональд Рівест (Ronald Linn Rivest), Аді Шамір (Adi Shamir) та Леонард Адлеман (Leonard Adleman) запропонували асиметричний алгоритм перетворення цілих чисел в цілі числа. Цей алгоритм отримав назву RSA за першими літерами прізвищ її авторів. В основі алгоритму − задача множення та факторизації простих чисел.

Алгоритм формування відкритого і секретного ключів згідно RSA наведено нижче:

1) випадковим образом обираються два простих числа і ( ), двійкове представлення яких має одну и ту саму довжину (ця умова забезпечує максимальну «безпеку» шифросистеми), яка не менша за біт;

2) випадковим образом обирається таке число , що і – взаємно прості числа, тобто

;

3) обчислюються числа і , де

і

.

Шифрування здійснюється в такий спосіб. Виділяємо в послідовності, що шифруємо, черговий фрагмент довжини меншої за і обчислюємо

. (4.1)

Розшифровка здійснюється у відповідності до формули

. (4.2)

Параметри і − секретний ключ, а може бути відоме всім. На сьогодні не відомий жоден поліноміальний алгоритм розкладання числа ( ) на два простих множники.

Можливі такі два варіанти:

I. Нехай – відкритий ключ, а – закритий ключ. Швидко зашифрувати повідомлення може будь-який користувач. Однак здійснити швидку розшифровку можуть лише ті користувачі, яким відомий секретний ключ.

II. Нехай – відкритий ключ, а – закритий ключ. Швидко розшифрувати шифротекст може будь-який користувач. Однак здійснити швидке шифрування можуть лише ті користувачі, яким відомий секретний ключ.

Приклад 4.1. Розглянемо роботу алгоритму RSA на прикладі.

1. Обираються два числа і . Ці числа тримаємо в таємниці.

2. Обчислюємо число . Це число може бути відоме всім.

3. Обчислюємо .

4. Обираємо відкритий ключ і . Нехай . Це число може бути відоме всім.

5. Обчислюємо секретний ключ і .

.

6. Зашифруємо текст за допомогою RSA.

.

Розшифруємо :

.

2. Завдання на проведення лабораторної роботи

2.1. Зашифрувати і розшифрувати тексти і відповідно за допомогою алгоритму RSA. Варіанти завдань, а також числа і наведені в таблиці 4.1. Відкритий ключ для шифрування обрати самостійно.

Таблиця 4.1 − Варіанти завдань

№ варіанта			відкритий текст	шифротекст

Лабораторна робота №5