Ковариационная матрица двумерной непрерывной случайной величины,коэффициенткорреляции,пределызначений,доказательство;независимость и некоррелированность:понятие и признаки. 3 страница

Математическое ожидание каждого слагаемого из первой группы (при i = j) равно .Математическое ожидание второй группы слагаемых (при i ¹ j) есть не что иное, как центральный смешаный момент порядка 1, 1, а это, как следует из п. 1.7.2, ковариация, которая вследствие независимости выборочных значений равна нулю.В результате получаем, что .Подводя окончательный итог, получаем .Таким образом мы выяснили, что в случае, когда математическое ожидание генеральной совокупности неизвестно, исследованная оценка смещена. При n ®¥ смещение оценки убывает до нуля, поэтому такая оценка является асимптотически несмещенной. Обнаруженное смещение корректируется простым умножением на n/(n-1), и мы получаем общеизвестную рабочую формулу для расчета несмещенной оценки дисперсии: .Обращает на себя внимание тот факт, что при количестве слагаемых, равном n, сумма делится на n-1. Это происходит потому, что каждое слагаемое содержит в себе одинаковые выборочные значения с коэффициентом 1/n, которые были использованы при вычислении среднего арифметического значения 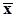, и значит, эти слагаемые не являются независимыми. Чтобы убедиться в этом, найдем ковариацию между . В силу несмещенности среднего арифметического, как оценки математического ожидания, математические ожидания каждого из этих сомножителей равно 0. Поэтому ,где 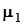- математическое ожидание генеральной совокупности.Первое слагаемое в последней сумме равно нулю в силу независимости выборочных данных. Второе слагаемое есть дисперсия среднего арифметического, которая равна 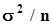. Третье и четвертое слагаемые равны друг другу, поэтому мы можем записать: .Вычитаемое здесь представляет сумму произведений биномов. Математическое ожидание всех этих произведений в силу независимости выборочных значений равно нулю, кроме тех, у которых совпадают индексы. Математическое ожидание таких произведений равно дисперсии 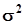, а их количество равно 1. Поэтому .Коэффициент корреляции равен .Как видим, данные биномы коррелированы, и значит, зависимы, что и требовалось доказать.Переведем отмеченное обстоятельство на общепринятый язык математической статистики. Принято говорить, что оценка 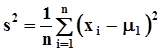имеет nстепеней свободы, а оценка - (n-1)степеней свободы.Этимологию этих понятий можно объяснить следующим образом.Если все выборочные значения независимы, то каждое из них обладает полной “свободой”. На n выборочных значений приходится n таких “свобод”. Столько же “свобод” приходится на n слагаемых первой из приведенных оценок дисперсии.Как только на слагаемые накладываются какие-либо зависимости, количество “свобод” уменьшается. Во второй оценке степень зависимости между каждыми двумя биномами вида мы оценили в 1/n, поэтому в совокупности от всех n таких биномов отнята одна целая “свобода”, и общее количество “свобод” или степеней свободы осталось (n-1). Потому в этой оценке сумма квадратов биномов делится на эквивалентное число оставшихся “свобод”.Это подтверждается также следующим соображением: по выборке объема n = 1,то есть по одному значению (при этом в знаменателе формулы будет 0) невозможно судить о разбросе значений случайных величин.

32.Плотность распределения “хи-квадрат”, график, понятие о степенях свободы, характеристическая функция, числовые характеристики, безграничная делимость, области применения.c)Плотность распределения оценки 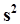.Будем считать, что выборка извлечена из нормальной генеральной совокупности с математическим ожиданием 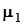и дисперсией 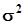.Рассмотрим вначале первую из оценок, несмещенную при априори известном математическом ожидании 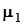. Преобразуем ее следующим образом: .Из п. 1.6.5. следует, что Это значит, что .В п. 1.6.7 мы нашли, что при возведении в квадрат нормальной случайной величины с параметрами (0, 1) получается новая случайная величина, плотность распределения и характеристическая функция которой равны соответственно .По свойству характеристических функций (см. п. 1.7.5), характеристическая функция суммы независимых случайных величин равна произведению характеристических функций слагаемых. В нашем случае характеристическая функция случайной величины равна . Плотность распределения этой случайной величины отыскивается обратным преобразованием характеристической функции и имеет следующий вид: .Полное название приведенной плотности: плотность распределения “хи-квадрат” сnстепенями свободы. Эта плотность распределения имеет всего один параметр: n - число степеней свободы.В справедливости этого выражения можно убедиться путем определения характеристической функции этой плотности.Принадлежность случайной величины z генеральной совокупности с плотностью распределения “хи-квадрат” и числом степеней свободы (n-1) мы будем обозначать так: .Найдем математическое ожидание и дисперсию случайной величины, распределенной по с помощью характеристической функции.Первая производная от характеристической функции по n : ,откуда .Вторая производная : ,

откуда .

В тех случаях, когда оценка дисперсии вычисляется при неизвестном математическом ожидании, количество степеней свободы уменьшается на единицу. Тогда случайная величина zраспределена в соответствии с плотностью распределения 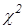с n-1степенями свободы: , Математическое ожидание и дисперсия этой случайной величины равны 1, .Плотность распределения имеет вид: .Характерная особенность плотности распределения : дисперсия равна удвоенному математическому ожиданию.Плотность распределения безгранично делима. В самом деле, пусть с характеристической функцией , и с характеристической функцией . Тогда характеристическая функция случайной величины есть , то есть это также характеристическая функция распределения с степенями свободы, а это значит, что .Еще раз напомним, что распределение получено нами при условии, что выборка изъята из нормальной генеральной совокупности. В свою очередь, распределение асимптотически нормально.2.3.4.3. Свойства оценки математического ожидания случайного вектораИз многомерной генеральной совокупности X , образованной случайным вектором с математическим ожиданием и ковариационной матрицей извлечена вы­борка векторов , которые попарно независимы в соответствии с исходным требованием математической статистики об обеспечении независимости выборочных данных.Несмещенной состоятельной оценкой математического ожидания каждой компоненты случайного вектора , как следует из п. 2.3.4.1, является среднее арифметическое значение, вычисленное по выборочным значениям соответствующих компонент выборочных векторов: , j = 1, 2, ..., k.Стало быть, несмещенной состоятельной оценкой математического ожидания является вектор, составленный из таких компонент: .Ковариационная матрица этого вектора равна .Это следует хотя бы из того, что каждый j - ый диагональный элемент матрицы , который является дисперсией каждого j - го компонента вектора средних арифметических , в n раз меньше дисперсии j - го компонента случайного вектора 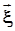, то естьj - го диагонального элемента ковариационной матрицы (см. п. 2.3.4.1): .Точно так же пропорционально изменяются и остальные элементы матрицы , поэтому .2.3.4.4. Оценка ковариационной матрицы случайного вектораИз многомерной генеральной совокупности X , образованной случайным вектором с математическим ожиданием и овариационной матрицей извлечена вы­борка векторов , которые попарно независимы в соответствии с исходным требованием математической статистики об обеспечении независимости выборочных данных.Оценкой ковариационной матрицы является матрица той же размерности, диагональные элементы которой суть оценки диагональных элементов матрицы , то есть дисперсий j - ых компонент случайного вектора 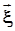. Желательно получить несмещенные оценки этих дисперсий, как и всех остальных элементов матрицы , то есть ковариаций. Вычисление оценки ковариационной матрицы выполняется в соответствии с ее определением (см. п. 1.8), где вместо символа математического ожидания, как и ранее, используется суммирование и усреднение. Поэтому несмещенная оценка ковариационной матрицы, все элементы которой должны быть несмещенными оценками матрицы , вычисляется по формуле: .В знаменателе этой формулы nуменьшается на единицу, как и в п. 2.3.4.2, поскольку каждый элемент матрицы “истратил” по одной степени свободы из-за предварительного вычисления среднего арифметического значения соответствующей компоненты. Кроме того при матрица будет особенной, поскольку ее определитель при этом оказывается равным 0.

33 билет.Метод максимального правдоподобия, оценки параметров нормального распределения методом максимального правдоподобия.2.3.5. Метод максимального правдоподобия (likelihoodmethod)Точечные оценки, полученные методом максимального правдоподобия (ММП - оценки), являются эффективными оценками, хотя и могут быть смещенными. Для получения ММП - оценок необходима априорная информация о плотности распределения.

Итак, пусть плотность распределения генеральной совокупности X известна с точностью до параметров 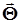, подлежащих оцениванию. Из этой генеральной совокупности извлечена выборка .

Образуем около каждого выборочного значения 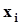непересекающиеся интервалы равной ширины, такие, чтобы каждое выборочное значение находилось в середине своего интервала (см. рис. 29). Обозначим ширину этих интервалов через Dx. Расчитаем вероятность того, что каждое из выборочных значений попадает в свой интервал, то есть

.В соответствии с принципом максимального правдоподобия в качестве оценок параметров 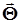предлагается найти такие значения параметров, при которых имеющаяся выборка оказывается наиболее правдоподобной или, что то же самое, наиболее вероятной. Для этого необходимо найти максимум указанной выше вероятности. Предварительно сделаем два упрощения. Первое из них - отбрасывание постоянных сомножителей Dx, как не влияющих на положение аксимума.

Второе – будем отыскивать максимум логарифма этой вероятности, ибо логарифмирование функции по основанию, большему единицы, не влияет на положение ее максимума, но в большинстве случаев приводит к значительному упрощению выкладок. В результате этих действий получим логарифмическуюфункцию правдоподобия: .ММП - оценки параметров 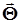находятся путем поиска максимума функции правдоподобия .Пример 1. Случайная величина xраспределена нормально: .Найти ММП - оценку математического ожидания случайной величины x по выборочным значениям .Функция правдоподобия для поставленной задачи

.

Будем отыскивать максимум функции правдоподобия с помощью производной по а. Первое слагаемое не зависит ота, поэтому его учитывать не будем. Остается найти максимум отрицательного выражения, который достигается там, где достигается минимум его абсолютной величины. Поэтому ММП - оценка математического ожидания есть значение, при котором достигается максимум функции правдоподобия: .Продифференцируем минимизируемое выражение по а и приравняем производную нулю: ,откуда сразу получаем ММП-оценку математического ожидания .Из этого факта с необходимостью следует эффективность среднего арифметического, как оценки математического ожидания по выборке, извлеченной из нормальной генеральной совокупности. Об этом уже было упомянуто выше в п. 2.3.4.1.Пример 2. Измерения одной и той же величины, значение которой равно a, выполняются различными средствами измерений, обладающими различными случайными погрешностями, среднеквадратические значения которых . Измерения, выполняемые каждым средством измерений, однократные, погрешности распределены нормально, систематические составляющие погрешностей отсутствуют. Найти ММП-оценку значения измеряемой величины.Подобная ситуация в математической статистике классифицируется, как случай неравноточных измерений, в отличие от примера 1, который классифицируется, как случай равноточных измерений.В этой ситуации каждое выборочное значение извлекается из своей генеральной совокупности, то есть . Функция правдоподобия теперь будет иметь иной вид, чем прежде: .Дифференцируем функцию правдоподобия по a и приравниваем производную нулю: ,откуда получаем ММП-оценку математического ожидания в случае неравноточных измерений: ,где веса обратно пропорциональны дисперсиям случайных погрешностей измерений и в сумме составляют единицу: , .Пример 3. Выборка извлечена из генеральной совокупности, распределенной по Лапласу. Плотность распределения .Найти ММП-оценки параметров a (математическое ожидание) и l.

Функция правдоподобия имеет вид: .

Найдем вначале ММП-оценку математического ожидания а. Поскольку первое слагаемое не содержит а, его значение не влияет на положение максимума, поэтому мы его исключим. Останется одно отрицательное слагаемое, минимум модуля которого совпадает по положению с максимумом функции правдоподобия. Поэтому будем отыскивать ММП-оценку путем поиска минимума суммы . Эта сумма недифференцируема, и нам придется находить искомую оценку с привлечением геометрических построений. Пусть в результате эксперимента получено всего три выборочных значения , которые разместились на вещественной оси так, как показано на рис.30.Каждое слагаемое минимизируемой суммы есть расстояние от каждого выборочного значения до математического ожидания. В ситуации, представленной на рисунке, одно из этих расстояний входит в сумму дважды. Это расстояние . Легко видеть, что рассматриваемая сумма достигнет минимума только тогда, когда оценка совместится с , то есть с выборочной медианой. Добавляя к этой небольшой выборке четное количество элементов, мы придем к тому же выводу, что ММП-оценкой атематического ожидания случайной величины, распределенной по Лапласу, является выборочная медиана, то есть .А это означает, что эта оценка эффективна.Теперь найдем ММП-оценку параметра l. Þ .Отсюда следует, что .2.3.6. Метод минимума Как и ранее в п. 2.3.5, ставится задача оценки параметров 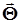плотности распределения 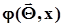, вид которой известен. Исходными данными являются выборочные значения, по которым строится гистограмма (см. п. 2.2, рис. 27). Идея метода заключается в подборе таких значений искомых параметров, при которых достигается минимальное отличие кривой плотности распределения от гистограммы. В качестве меры этого отличия чаще всего используется квадратичный функционал, наиболее удобный для реализации аналитических и численных методов поиска экстремума (минимума или максимума).В нашей задаче в качестве такого функционала используется сумма, обозначенная здесь и далее, как . О причине такого обозначения станет ясно в дальнейшем из материала п. 2.5.5.1. ,В этой сумме K - общее количество интервалов, на которых построена гистограмма, n - объем выборки, - количество выборочных значений, попавших в k - ый интервал гистограммы, - вероятностная мера k - го интервала гистограммы: .Эти обозначения иллюстрируются рис. 38 п. 2.5.5.1.Таким образом, слагаемые этой суммы представляют собой квадраты разностей между вероятностными мерами k - ых интервалов, порожденными генеральной плотностью распределения, и частотными оценками этих вероятностных мер. Знаменателем каждого слагаемого является вероятность , благодаря чему в процессе поиска значений параметров 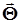повышается вес интервалов с низкой вероятностью и тем самым обеспечивается повышенная точность подгонки в области этих интервалов. Как правило, эти интервалы находятся на удалении от центра распределения (на так называемых “хвостах” распределений).Вероятности суть функции от искомых параметров 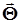, от тех же параметров зависит и величина , и процедура оценивания параметров по методу минимума формально записывается в виде: .В большинстве случаев этот минимум и оценки находятся численными методами. Доказано (см., например, [4] стр. 461, 549 и [5], стр.303), что оценки, полученные методом минимума , обладают свойствами, сопоставимыми со свойствами ММП - оценок, а именно, эти оценки ассимптотически эффективны.