Жай сандардың шексіз көптігі
Енді жай сандар не бары қанша деген мәселеге келейік. Бұған Евклидтің мынандай теоремасы жауап береді.
21-теорема.(Евклид теоремасы). Натурал сандар жиынындағы жай сандар саны ақырсыз.
Дәлелдеуі. Теореманы дәлелдеу үшін кері жору тәсілін қолданамыз. Айталық, натурал сандар жиынындағы жай сандардың саны ақырлы делік және оларды  деп белгілейік, мұндағы
деп белгілейік, мұндағы  ең үлкен жай сан.
ең үлкен жай сан.
Мынандай  санын құрайық.
санын құрайық.  болғандықтан,
болғандықтан,  саны құрама сан. Демек ол бір жай санға бөлінуге тиіс. Ал ұйғарым бойынша барлық жай сандар
саны құрама сан. Демек ол бір жай санға бөлінуге тиіс. Ал ұйғарым бойынша барлық жай сандар  сандары. Ендеше
сандары. Ендеше  саны осы сандардың біріне бөлінуі тиіс. Ол
саны осы сандардың біріне бөлінуі тиіс. Ол 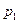 саны дейік.
саны дейік.  көбейтіндісі де,
көбейтіндісі де,  саны да
саны да 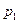 -ге бөлінетіндіктен, бөлінгіштііктің қасиеті бойынша, бір саны
-ге бөлінетіндіктен, бөлінгіштііктің қасиеті бойынша, бір саны 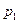 -ге бөлінуі тиіс. Бұлай болуы мүмкін емес, өйткені
-ге бөлінуі тиіс. Бұлай болуы мүмкін емес, өйткені  Демек біз жасаған ұйғарым дұрыс емес. Сонымен, жай сандардың саны ақырсыз.
Демек біз жасаған ұйғарым дұрыс емес. Сонымен, жай сандардың саны ақырсыз.
Сандардың натурал қатар айырымы 1-ге тең ақырсыз арифметикалық
прогрессия құрайтын белгілі. Ендеше, Евклид теоремасын тағы былай да тұжырымдауға болады: айырымы 1-ге тең ақырсыз арифметикалық прогрессия құрамында ақырсыз көп жай сан бар. 19 ғасырдың белгілі математигі Л. Дирехле (1805-1859) Евклид теоремасын былайша жалпылады: әрбі

арифметикалық прогрессиядағы жай сандар саны ақырсыз. Мұндағы  .
.
22-теорема. Егер  жай саны
жай саны  құрама санының ең кіші бөлгіші болса, онда
құрама санының ең кіші бөлгіші болса, онда 
Дәлелдеуі.  болғандықтан, бүтін
болғандықтан, бүтін  саны табылып
саны табылып  теідігі орындалады. Ал
теідігі орындалады. Ал  ең кіші бөлгіші болғандықтан
ең кіші бөлгіші болғандықтан  Осы теңсіздіктің сол жағын
Осы теңсіздіктің сол жағын  ал оң жағын
ал оң жағын  санына көбейтсек,
санына көбейтсек,  болғандықтан,
болғандықтан,  болады. бұдан
болады. бұдан  Яғни,
Яғни,  санының жай бөлгіші
санының жай бөлгіші  санынан кіші. Егер
санынан кіші. Егер  саны
саны  санынан кіші жай сандардың ешқайсысына бөлінбесе, онда
санынан кіші жай сандардың ешқайсысына бөлінбесе, онда  жай сан болған.
жай сан болған.
Мысалы, 59 саны жай сан. Өйткені ол  -дан кіші жай 2,3,5,7
-дан кіші жай 2,3,5,7
сандарының ешқайсысына бөлінбейді.
Эратосфен торы
Натурал қатардан жай сандарды бөліп көрсету үшін Эротосфен торы деп аталатын тәсіл бар (Эротосфен грек математигі, біздің жыл санауымызға дейін 3 ғасырда өмір сүрген).
Эротосфен тәсілі мынадай қарапайым жағдайға негізделген: өзінен кіші жай сандардың ешқайсысымен де еселі емес сан, жай сан болады. Натурал сандар қатарын жазайық:
1,2,3,4,5,6,7,8,9,10....
Енді 2-ге тимей оған еселі сандардың барлығын сызайық, сонда 2-ден бастап санағанда әрбір келесі екінші санды, яғни 4,6,8,10... сандарды сызамыз. 2-ден кейінгі сызылмай қалған 3 саны жай сан болады. Енді қатарда қалған
2,3,5,7,9,11,13,15,17,19,21,...
сандары ішінен 3-ке тимей, оған еселі сандарды сызып шығамыз, сонда біз 3-тен бастап есептегенде әрбір 3-ші санды, яғни 9,15,21,... сандарды сызамыз. 3-тен кейінгі сызылмай қалған 5 саны да, жай сан. Енді қатардағы қалған сандардың ішінен 5-ке еселерін сызып шығамыз т.с.с.
Құрама сандарды әрі қарай да осылайша сызу процесін орындай келе, біз натурал қатардың барлық жай сандарын табамыз. Эротосфен торы онша қолайлы болмаса да, натурал қатардың тетелес жай сандарын табу үшін қолданылады.
