Основные объекты (определение, ввод, действия с ними).
ЛЕКЦИЯ № 5 Основные объекты и команды Maple V
5.1 Основные объекты (определение, ввод, действия с ними).
5.2 Внутренняя структура объектов Maple.
5.3 Подстановка и преобразование типов.
5.4 Встроенные элементарные математические функции.
5.5 Команды преобразования выражений.
5.6 Операции и функции математического анализа.
Основные объекты (определение, ввод, действия с ними).
 | Числа. |
Maple V работает с числами следующего типа:
- целыми десятичными (О, 1, 123, -456 и т.д.),
- рациональными в виде отношения целых чисел (7/9, —123/127 и т.д.),
- радикалами,
- вещественными с мантиссой и порядком (1.23E5, 123.456E-10)
- комплексными (2+3*I)
Целые числа задаются в виде последовательности цифр от 0 до 9.
 | Maple может работать с целыми числами произвольной величины, количество цифр практически ограничено числом 228. Большие числа, которые не помещаются на одной строке области вывода, Maple переносит на следующую строку, используя символ обратного слэша (\).
|
Получить список всех команд для работы с целыми числами можно, набрав команду:
?integer. Приведем некоторые из этих команд:
| ifactor | разложение на простые множители |
| iquo | вычисление частного при операции целого деления |
| irem | вычисление остатка при операции целого деления |
| igcd | нахождение наибольшего общего делителя двух целых чисел |
| isprime | проверка, является ли целое число простым |
Обыкновенные дроби задаются с помощью операции деления лвух целых чисел.
 | Заметим, что Maple автоматически произвадит сокращение дробей. Над обыкновенными дробями можно выполнять все основные арифметические операции. Если при задании дроби ее знаменатель сокращается, то такая "дробь" трактуется программой Maple как целое число. Для преобразования обыкновенной дроби в десятичную служит команда evalf( ). Второй параметр этой команды задает число значащих цифр. Заметим, что десятичное представление всего лишь аппроксимация точной величины, представленной обыкновенной дробью, т.е. дробь и ее десятичное представление не являются идентичными объектами Maple. |
Радикалы задаются как результат возведения в дробную степень целых или дробных чисел, или вычисления из них же квадратного корня функцией sqrt( ), или корня n-ой степени функцией surd(число, n).
 | В Maple возведение в степень задается символом (^) или последовательностью двух звездочек (**). При задании радикалов также производятся всевозможные упрощения, связанные с вынесением из-под знака радикала максимально возможной величины. Вычисления с целыми, дробями и радикалами являются абсолютно точными, так как при работе с этими объектами Maple не производит никаких округлений в отличие от чисел с плавающей точкой. |
Числа с плавающей точкой задаются в виде целой и дробной частей, разделенных десятичной точкой. Их можно представить также, используя так называемую экспоненциальную форму записи ( для указания порядка применяется символ e или E).
 | Если в выражении присутствует число с плавающей точкой, то результатом вычисления такого "смешанного" выражения будет число с плавающей точкой. Если в выражении присутствует радикал, то он вычисляется точно, а коэффициент при нем вычисляется либо точно, либо в виде числа с плавающей точкой в зависимости от вида сомножителей. |
| Комплексные числа. Для мнимой единицы в Maple используется константа I. Задание комплексного числа ничем не отличается от его обычного задания в математике ( например 2+3*I или d+k*I). Если хотя бы одна из частей комплексного часла (действительная или мнимая) вычисляются в виде числа с плавающей точкой, то и результат будет таким же. Некоторые команды для работы с комплексными числами: |  |
| Re( ) | выделение действительной части комплексного числа |
| Im( ) | выделение мнимой части комплексного числа |
| argument( ) | вычисление аргумента комплексного числа |
| conjugate( ) | построение комплексно-сопряженного числа |
 | Константы. |
Maple содержит целый ряд предопределенных именованных констант - таких, к значениям которых можно обращаться по имени. Часть этих констант не может быть изменена. К ним относятся:
| false | -логическое значение "не истинно"; |
| gamma | -константа Эйлера (0.5772156649..); |
| infinity | -положительная бесконечность; |
| true | -логическое значение "истинно"; |
| Catalan | -константа Каталана (0.915965594..); |
| FAIL | -специальная константа, используется в качестве третьего значения при вычислении функций трехзначной логики; |
| I | -мнимая единица; |
| Pi | -константа р=3.141.. |
Число е задается как exp(1).
 | Константы, значения которых могут быть переопределены:
|
Посмотреть все константы, определенные в Maple, можно, исполнив команду: ?ininame
Кроме перечисленных на странице Справки констант все переменные, имена которых начинаются с _Env, по умолчанию являются системными константами Maple.
 | Строки. |
Строки - любой набор символов, заключенный в ДВОЙНЫЕ кавычки. Длина строки в Maple практически не ограничена и может достигать на 32-битных компьютерах длины 268 435 439 символов.
 | Если идут подряд две строки, разделенные символами-разделителями (пробел, табуляция или переход на новую строку), то в обрасти вывода эти две строки соединяются в одну, причем, без пробела между ними. Соединение строк можно осуществить и с помощью операции конкатенации ||, или обращением к функции cat(строка 1, строка 2). Строка представляется как одномерный массив, поэтому можно использовать индекс (или диапазон) для выделения элемента (или подстроки) из заданной строки. |
 | Переменные, неизвестные и выражения. |
Каждая переменная Maple имеет имя, представляющее последовательность латинских символов, начинающихся с буквы, причем строчные и прописные буквы считаются различными. Кроме букв в именах переменных могут использоваться цифры и знак подчеркивания, но ПЕРВЫМ символом имени должна быть БУКВА.
 | В качестве имен запрещено использовать зарезервированные слова языка Maple (см. Лекцию 1), а также защищенные слова (справку по ним можно получить, выполнив команду ?protect). В Maple можно задавать переменные с именами, содержащими пробелы, но для этого их следует заключать в обратные кавычки. |
Выражение представляет собой комбинацию имен переменных, чисел и, возможно, других объектов Maple, соединенных знаками допустимых операций.
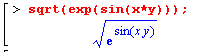 | Если в выражении используется переменная, которой не присвоено никакого числового значения, то такая переменная рассматривается системой Maple как |
неизвестная величина, а выражение, содержащее неизвестные, называется символьным выражением. Именно для работы с такими выражениями прежде всего и разрабатывался Maple.
Важной операцией в Maple, связанной с выражениями, является операция присваивания (:=). Она имеет следующий синтаксис:
переменная := выражение;
Здесь в левой части задается имя переменной, а в правой - любое выражение, которое может быть числовым, символьным или просто другой переменной.
Переменные позволяют хранить и обрабатывать разнообразные типы данных. При этом по умолчанию переменная Maple имеет тип symbol, представляющий символьную переменную, и ее значением является ее собственное имя. При присвоении переменной какого-нибудь значения, ее тип изменяется на тип присвоенного ей значения.
| Последовательности, списки, множества. |
Последовательность - это ряд выражений, разделенных запятыми и завершенных фиксатором:
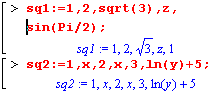 | Последовательность является базовым объектом Maple, на основе которого строятся другие сложные объекты. Последовательность сохраняет порядок следования выражений и может содержать повторяющиеся элементы. |
Ее можно мыслить как последовательность выражений, перенумерованных натуральными числами, начиная с единицы.
| В связи с этим, можно получить значение любого элемента последовательности, используя индексную форму записи - после имени переменной в квадратных скобках задать индекс элемента. Однако присвоить новое значение элементу последовательности с использованием индексной формы обращения нельзя. |  |
Использование последовательностей.
 | 1. Если этот тип данных передается в качестве параметра функции Maple, то каждый элемент рассматривается как соответствующий параметр функции. (Пример с вычислением интеграла.) 2. Использование последовательности в качестве одного из операндов приводит к выполнению этой операции для каждого ее элемента в качестве соответствующего операнда и формирования новой последовательности.(Пример с созданием новой последовательности) |
3. Использование последовательности переменных в ЛЕВОЙ части операции присваивания и последовательности значений в ПРАВОЙ приводит к множественному присваиванию с помощью одной операции.
Создание последовательностей. Для создания длинных последовательностей, элементы которых подчиняются некоей закономерности, можно использовать каманду seq( ) и операцию повторения $.
| 1) Команда seq( ) имеет две формы: seq(f,i=m..n) seq(f,i=X)В них f - выражение, зависящее от переменной, имя которой определяется параметром i, m и n -числа, определяющие диапазон изменения переменной i с шагом 1, X может быть списком, множеством, суммой, произведением или строкой. (В последнем случае переменная i последовательно принимает значения, равные символам строки). | 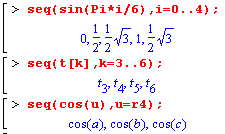 |
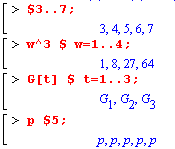 | 2) Операция повторения $ может быть унарной и бинарной. В первом случае она применяется к диапазону m..n, где m и n - числа; а во втором случае первым операндом является выражение, зависящее от переменной, которая указана во втором операнде, содержащем также операцию диапазон. |
| Список - упорядоченная последовательность выражений, заключенная в квадратные скобки. Множество - неупорядоченная последовательность выражений, заключенная в фигурные скобки. | 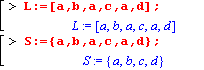 |
Свойства списка:
- В списке все повторяющиеся элементы существенны, т.е. список может содержать повторяющиеся элементы, стоящие на разных местах.
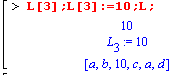 |
|
Свойства множества:
- В множестве все повторяющиеся элементы игнорируются, т.е. повторяющимся элементам последовательности во множестве будет соответствовать один элемент.
 |
|
- Индексной форме элемента списка НЕЛЬЗЯ присвоить новое значение. Чтобы изменить элемент множества, его следует удалить операцией minus, а затем добавить новый элемент операцией union (разность и объединение).
При выборе нескольких элементов списка или множества и помощью индекса можно использовать объект диапазон, причём положительные значения индекса соответствуют отсчету элементов слева направо, а отрицательные -справа налево. Все элементы списка или множества можно вывести, указав в качестве индекса диапазон [1..-1]. (Значение индекса равное -1 соответствует последнему элементу списка или множества.)
Команды для структурной обработки списков и множеств. Часто возникает необходимость выполнить какую-либо команду или вычислить функцию применительно к каждому элементу списка или множества; выделить элементы, удовлетворяющие некоторому условию и др.
Команды map( ) и map2( ) позволяют применить функцию или команду, заданную первым параметром, ко всем элементам списка или множества, возвращая, соответственно, список или множество. Синтаксис этих команд:
map(функция, список| множество, [пар2, пар3,..., парN]);
map2(функция, пар1,список|множество, [ пар3,..., парN]);
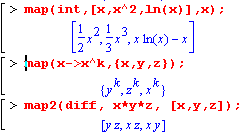 | Если для выполнения функции, заданной первым параметром команды map ( ), необходимы дополнительные параметры, то их следует задать после списка или множества. В команде map2( ) элементы списка или множества передаются в качестве второго параметра функции, определенной первым параметром. |
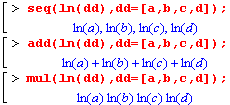 | Команда seq( ) формирования последовательности может также поэлементно обрабатывать список или множество, формируя при этом (в зависимости от вида скобок или их присутствия/отсутствия) список, множество или последовательность. |
Команда add( ) формирует сумму элементов списка или множества, команда mul( ) - произведение элементов списка или множества.
 | Maple позволяет выбирать из списка или множества элементы, удовлетворяющие некоторому условию. Для этого прежде всего необходимо определить функцию-условие, результатом работы которой будет булево значение true или false. А затем можно воспользоваться команодой select(функция-условие, список|множество ) Действие команды remove(функция-условие, список|множество) противоположно действию команды select( ). |
Она возвращает список/множество, состоящий из элементов, не удовлетворяющих условию булевой функции.
Выполнить обе операции одновременно позволяет команда selectremove( ), которая возвращает последовательность двух списков, первый из которых представляет результат выполнения команды select( ), а второй – команды remove( ).
Линейное объединение двух списков можно реализовать с помощью команды op(выражение|список|множество ). Эта команда предназначена, вообще говоря, для выделения операндов выражения в виде последовательности. Так как операндами списка или множества являются его элементы, то результатом работы этой команды со списком| множеством будет последовательность, которую можно "оформить" с помощью скобок в виде множества или списка.
Более сложные объединения списков реализуются командой zip( ), имеющей следующий синтаксис:
zip(бинарная функция, список1, список2);
zip(бинарная функция, список1, список2, значение);
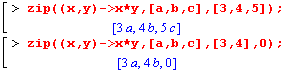 | Первая из команд работает так: бинарная (двух аргументов) функция выполняется, последовательно используя в качестве своих параметров элементы двух списков, формируя новый список из вычисленных значений. |
Длина полученного списка равна длине наименьшего из переданных (список1 и список2).
Вторая команда работает аналогично, но заданный четвертый параметр (значение) используется в качестве элементов списка наименьшей длины при продолжении последовательного выбора элементов списка большей длины. Т.е. короткий список дополняется элементами "значение" до длины большего списка. Таким образом, команда zip( ) формирует список , длина которого равна длине наибольшего списка-параметра.
 | Массивы. |
Массив является дальнейшим развитием концепции списка. Если список можно мыслить как перенумерованную последовательность, индексы которой могут принимать только положительные целые значения (нумерация обязательно начинается с единицы), то в массиве каждый элемент также связан с индексом, однако не ограничен одной размерностью (массив может иметь много размерностей, каждую со своим индексом), причем индексы могут принимать наряду с целыми положительными и отрицательные значения, и нуль.
Создание массивов.. Создать массив в Maple можно несколькими способами. Простейший из них - использование функции array( ) стандартной библиотеки. Синтаксис создания массива следующий:
array(границы, список, опции );
Параметр границы представляет диапазон(ы) изменения индекса(ов) массива (для многомерного массива диапазоны задаются через запятую).
 | Список задает значения элементов массива, причем для двумерного массива элементами списка являются списки, т.е. этот параметр является списком списков. Параметр опции используется для задания массивов специального вида. Этот параметр может принимать следующие значения: symmetric, antisymmetric, sparse, identity, diagonal , для задания , соответственно, симметричных, антисимметричных, разреженных, единичных и диагональных массивов. |
Все пераметры этой функции являются необязательными, однако, либо параметр границы, либо список значений должен обязательно присутствовать.
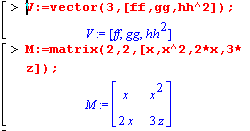 | Для задания вектора и матрицы можно использовать соответственно команды vector( ) и matrx( ). Синтаксис этих команд: vector(n,[элемент1, элемент2, ...] ); matrx(n, m, [элемент1, элемент2, ...] ) Здесь целые величины n и m задают размерности вектора и матрицы, а значения их элементов задаются в виде простого списка. |
 | Значения элементов вектора или матрицы не обязательно задавать при создании этих объектов. Можно позднее с помощью индексной ссылки на элементы вектора или матрицы (в квадратных скобках) присвоить им значения. Для отображения содержимого вектора или матрицы используется команда print(V) или eval(V), так как переменная, содержащая сложные объекты, вычисляется не полностью, а только до своего имени. |
 | Для отображения результатов ВЫЧИСЛЕНИЙ с матрицами и векторами служит команда evalm(V). Эта команда отображает результат вычислений на уровне элементов. Над матрицами и векторами (без подключения специальных пакетов linalg и LinearAlgebra) возможны любые действия, заданные операторами сложения (+), вычитания (-), некоммутативного умножения (&*), деления (/) и возведения в степень (^). Пакеты linalg и LinearAlgebra содержат множество функций для структурных преобразований матриц и векторов, команд выполнения матричных операций. Перечень всех доступных команд можно найти на страницах справки, отображаемых командами ?linalg (для пакета linalg) и ?LAOverview (для нового пакета LinearAlgebra, а дальше - путешествуйте по ссылкам, находящимся на этой странице). |
 | Таблицы. |
Таблица является дальнейшим развитием массива, как структуры данных. В ней в качестве индекса можно использовать не только целые числа, а всё, что угодно. Для создания таблицы используется функция table( ). Её параметрами являются индексная функция (см. параметр опция для команды array( ))и список или множество пар индекс=значение. Первый параметр необязательный.
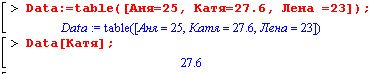
Таблицы достаточно удобный объект, когда в одном "массиве" надо хранить данные, относящиеся к какому-либо реальному объекту, и ссылаться на них по индексам, представляющим естественную запись их наименований. Maple выводит элементы таблицы в произвольном порядке, но, используя соответствующий индекс, можно получит значение любого элемента таблицы.

