Задания к лабораторной работе №11

Лабораторная работа №11

Решение уравнений и неравенств в Mathcad

Теоретические сведения

Решение уравнений

Многие задачи, с которыми приходилось сталкиваться в школьном курсе математики, задавались и решались в символьном виде. Тем или иным образом преобразовывались и упрощались выражения, использовались определенные стандартные формулы и методы, умножались, делились, сокращались – и в результате выражения приводились к какому-то несложному аналитическому результату. Так, например, при решении квадратного уравнения использовались формулы Виета. Пытаясь аналитически найти корни кубического уравнения, исходные выражения разлагались на линейные множители (или, в крайнем случае, использовали формулу Кардано). Для бикубических уравнений заменялся квадрат искомой переменной новой переменной, и в результате получалось квадратной уравнение.

Решение задач в аналитическом виде имеет массу преимуществ перед решением численным способом.

Во-первых, в этом случае ответ может быть вычислен без какой-либо погрешности.

Во-вторых, при получении результата в виде аналитического выражения имеются куда более широкие возможности его последующего использования (например, в качестве формулы).

В-третьих, числовой результат, полученный при вычислении выражения, представленного в символьном виде, куда более нам понятен, чем десятичная дробь, получаемая при использовании численных методов. Увы, но аналитическим решением обладает очень ограниченное количество задач.

Уравнение в первоначальном понимании – это равенство двух функций f₁(x) = f₂(x), рассматриваемых в общей области их определения. При желании это равенство можно записать в виде f(x) = 0, где f(x) = f₁(x)–f₂(x). Такой вид называют стандартным.

Решить уравнение – это значит, найти точки, в которых функция f(x) принимает нулевые значения.

В Mathcad реализовано три принципиально отличающихся друг от друга подхода к решению уравнений:

1) использование символьных преобразований,

2) применение численных алгоритмов,

3) графический метод.

Чтобы найти корни уравнения в виде выражения (т.е. при помощи символьных преобразований), требуется выразить одну переменную через все остальные. Обычно это можно сделать только в том случае, если уравнение включает переменные невысокой степени и не содержит разнородных функций. Такие уравнения специально подбираются в учебниках, и их можно более или менее просто решить. Вследствие чего возникает ложное представление о возможности аналитического решения любого уравнения (или системы уравнений).

Но на практике часто необходимо решать уравнения, которые абсолютно бесперспективно решать с помощью символьных преобразований. Численно же можно решить практически любое уравнение. Однако, численные методы достаточно трудоемки и получаемое при использовании численного метода значение корня в виде числа с плавающей точкой, куда менее информативно, чем выражение аналитического решения. Опыт показывает, что простые уравнения лучше решать в символьном виде, более сложные – численно. Обычно численный метод используется, если Mathcad не может решить уравнение аналитически (т.е. символьно).

Имеются такие уравнения, которые нельзя решить ни аналитически (так как они слишком сложны), ни численно (чаще всего потому, что соответствующая функция не является непрерывной). В таких случаях решение ищут по графику, используя специальные инструменты панели Graph (Графические). Данный способ довольно трудоемок, однако он способен обеспечить точность, мало уступающую точности численных методов.

Для численного решения нелинейного уравнения f(x)=0 можно использовать встроенную функцию root(ее вызов представлен на рисунке 47) и блок решения Given – find… .

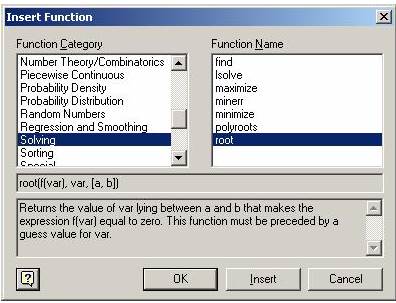
Рисунок 47 – Окно мастера функций, открытое для вызова функции root

Пример 1

Найти корень уравнения вида x∙(x –6)(x + 3)∙(5 – x) – 17 = 0 в численном виде при начальном значении x=0 и заданной точности 10³.

Решение

Процесс решения задачи можно свести к выполнению следующих шагов:

· Определить функцию для решения.

· Задать начальное значение корня.

· Переустановить точность – в данном случае не требуется, так как она соответствует точности, взятой «по умолчанию».

· Вызвать функцию root для решения.

Фрагмент с решением задачи в системе представлен на рисунке 48.

Рисунок 48 – Поиск корня уравнения с использованием функции root (в численном виде)

Пример 2

Найти корни уравнения

f (x) = 0 , где .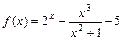

Решение

Прежде чем использовать функцию root,необходимо определить приближенное (начальное) значение корня. Для этого воспользуемся графическим методом.

Определим функцию f(x). Затем, экспериментально изменяя область определения функции, исследуем общую динамику изменения графика функции. Из рисунка 49 видно, что функция f(x) может пересекать ось абсцисс в точках, расположенных достаточно «близко» к точке ноль. Для более подробного исследования поведения функции в «районе» нуля увеличим интересующую нас область графика функции. Для этого щелкнем левой клавишей мыши по кнопке расположенной на панели Graph.

После этого появится дополнительное диалоговое окно X-Y Zoom. Подведем указатель мыши в левый верхний угол выделяемой области на графике, нажмем левую кнопку мыши и протянем мышь вниз и вправо. На графике выделенная область будет отмечена пунктирной линией. Отпустим левую кнопку мыши и нажмем в диалоговом окне кнопку Zoom.

Построится график выделенной области (рисунок 50). В этой области можно таким же образом задать новую область и так далее.

Кнопка Unzoom возвращает на одну выделенную область назад. Кнопка Full View восстанавливает исходную область графика. На рисунке 50 видно, что исходное уравнение имеет два корня. Сначала определим приближенное значение левого корня. Это можно сделать при помощи инструмента трассировки, который вызывается щелчком левой клавиши мыши по кнопки панели Graph. В результате появится окно трассировки X-Y Trace. Установим флажок Track Data Points (выбирается ближайшая линия графика к указателю мыши). Указатель мыши поместим в нужную точку графика (эта точка будет отображаться на пересечении двух пунктирных линий). В окне трассировки появятся координаты отмеченной точки графика. Эти координаты можно переместить в буфер обмена и потом поместить их в документ Mathсad или другой документ, например Word (рисунок 51).

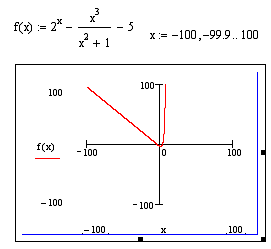
Рисунок 49 – Функция f(x) и ее график

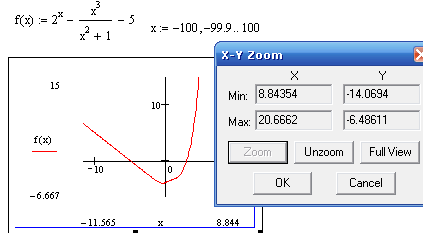
Рисунок 50 – Функция f(x) и ее график

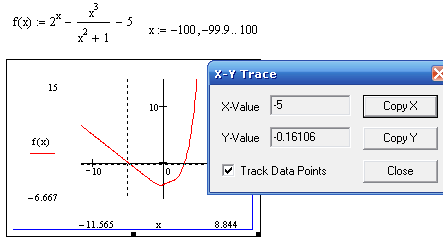
Рисунок 51 – Функция f(x) и ее график

После того как при помощи трассировки найдено приближенное значение левого корня, равное -5 (см. окно трассировки на рисунке 51), можно уточнить его с помощью функции root. Аналогично поступим с правым корнем. В итоге получим два корня исходного уравнения (рисунок 52).

Рисунок 52 – Использование функции root для уточнения корней уравнения

Для символьного(аналитического)решения уравнений в системе Mathcad можно воспользоваться одним из двух способов:

1. С помощью оператора solve(решить) (панель Symbolic(Символьные)).

2. С помощью команды solve (подменю Symbolics→Variable).

В первом случае для нахождения корня уравнения, необходимо выполнить следующую последовательность действий:

1) Введите оператор solve (панель Symbolic(Символьные)). В результате будет представлен шаблон вида:

В левом маркере задайте вид решаемого уравнения.

В качестве знака равенства следует использовать логическое равенство (панель Boolean, BoldEqual – вводится сочетанием <Ctrl>+<=>).

Если уравнение приведено к стандартному виду, то достаточно будет в этот маркер вписать лишь его левую часть. При этом выражение будет приравнено к нулю автоматически. Также в левый маркер можно внести и имя функции – в этом случае будут найдены выражения, определяющие ее нули. Форма записи уравнения через функцию удобна в том случае, если оно имеет большую длину.

2) В правый маркер внесите переменную, относительно которой должно быть решено уравнение, как это показано на рисунке 53.

Ответ оператор solve возвращает в виде выражения (численного или буквенного), которое вполне можно использовать в дальнейших вычислениях. Если решений имеется несколько, то возвращается содержащий их вектор.

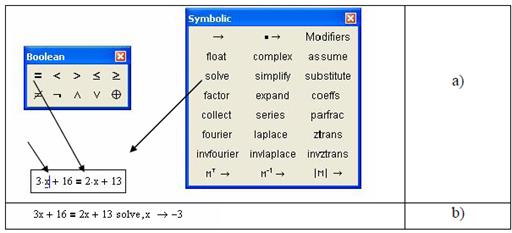
Рисунок 53 – Символьное решение уравнения с использованием панели инструментов Symbolic

При символьном решении уравнений нет особой разницы, сколько переменных содержит уравнение. Поиск ответа производится в виде выражения, и поэтому для системы неважно, будет ли оно содержать буквенные или численные элементы. Исходя из этого, вы можете найти корни как уравнения нескольких переменных, так и уравнения с параметрами или буквенными коэффициентами.

Во втором случае, чтобы решить уравнение в символьном виде, нужно ввести уравнение (знак <=> следует брать с панели Boolean), выделить переменную, выбрать команду solve из подменю Symbolics→Variable, как это показано на рисунке 54.

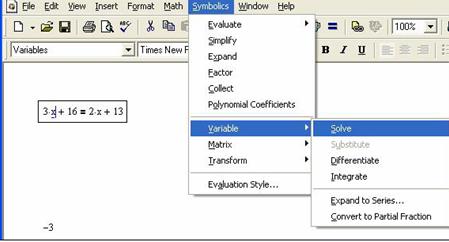
Рисунок 54 – Символьное решение уравнения с использованием подменю Variable

Пример 2

Требуется найти корни уравнения вида sin³(t)+cos³(t∙a)=1 в символьном виде. Следует иметь в виду, что при решении тригонометрических уравнений система находит только частное решение при n=0.

Решение

Процесс решения задачи можно свести к выполнению следующих шагов:

1. Выполнить команду solve, расположенную на панели Symbolics (Символьные).

2. Заполнить предоставленный шаблон.

3. Проанализировать результат, предоставленный системой в виде, как это показано на рисунке 55.

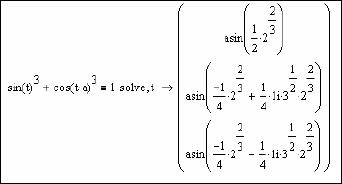
Рисунок 55 – Символьное решение уравнения с использованием команду solve

Как это видно из предоставленного системой решения, уравнение имеет три корня – один действительный и два комплексных. Ответ в аналитическом виде не всегда является удобным для анализа, поэтому пересчитываем его с помощью команды float,расположенной на панели Symbolics(Символьные), в десятичную дробь с точностью до 4 знаков:

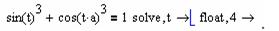
В результате решение примет вид, как это показано на рисунке 56.

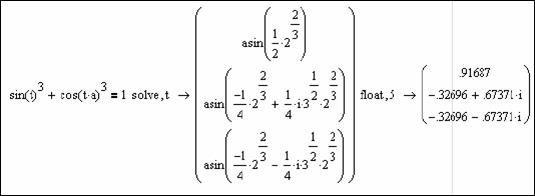
Рисунок 56 – Символьное решение уравнения с использованием команд solve и float

Пример 3

Требуется найти корни уравнения вида 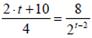в символьном виде.

Решение

Процесс решения, как это показано в предыдущей задаче, можно свести к выполнению следующих шагов:

1.1. Выполнить команду solve, расположенную на панели Symbolics(Символьные).

1.2. Заполнить предоставленный шаблон.

1.3. Результат решения предоставлен на рисунке 57.

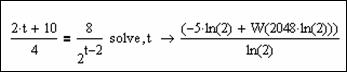
Рисунок 57 – Символьное решение уравнения с использованием команд solve

В предоставленном решении используется ссылка на функцию с именем W – функцию Ламберта. Функция Ламберта – это функция обратная функции f(x) = x – e^x. Чтобы найти значение W и использовать найденное значение в предоставленном решении, можно также воспользоваться оператором float, как это показано на рисунке 58.

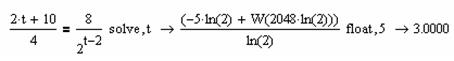
Рисунок 58 – Символьное решение уравнения с использованием команд solve и float

Пример 4

Требуется найти корни уравнений вида:

а) log2(x + 2)2+ log2(х+10)2= 4∙log2 3,

б) lg(1–x)+lg(x–4)–lg(x2–5x+ 6)=2

в символьном виде. Здесь log₂– логарифм по основанию 2, a lg– логарифм по основанию 10.

Решение

Выполняется по стандартной схеме, как это показано в предыдущих примерах. Результаты решения представлены на рисунке 59.

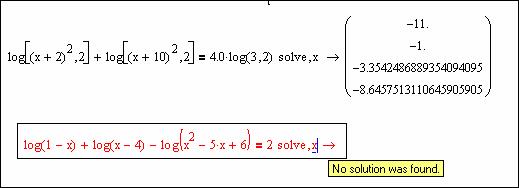
Рисунок 59 – Символьное решение уравнений с использованием команды solve

Как это видно из рисунка 59, первое уравнение имеет 4 действительных корня, а второе уравнение не имеет решение – об этом система выдала сообщение (при этом цвет символов в уравнении изменился на красный, а сообщение об отсутствии решения поместилось в прямоугольную область желтого цвета). Действительно, анализ области определения для уравнения 2 (приведен на рисунке 60) показывает, что эта область пуста, т.е. нет таких значений x, при которых имелось бы решение уравнения. Поэтому при решении уравнений целесообразно предварительно находить область определения функции.

Рисунок 60 – Построение области определения для функции b) из примера 4

Решение неравенств

Пример 5

Требуется решить неравенство вида в символьном виде:

.

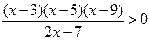Решение

Процесс решения задачи можно свести к выполнению следующих шагов:

1. Выполнить командуsolve (панели Symbolics(Символьные)).

2. Заполнить предоставленный шаблон.

3. Проанализировать результат.

Решение неравенства предоставлено системой на рисунке 61. Полученное решение соответствует следующей записи в стандартной форме:

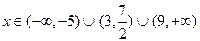
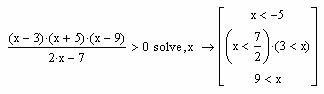
Рисунок 61 – Решение неравенства

Mathcad выдает ответы в несколько отличном, от принятого в нашей математике виде. Поэтому зачастую самой трудной частью работы при символьном решении неравенств является интерпретация результата. Тут нужно запомнить несколько правил:

1. Ответ операторsolve возвращает в виде вектора, содержащего элементарные неравенства. Каждое такое неравенство описываетобласть, в которой решаемое неравенство справедливо.

2. Если область открытая (то есть одной из ее границ является бесконечность), то задающее ее элементарное неравенство будет иметь вид х>а или х<а. В стандартном виде такие области запишутся как (а,+∞) или (-∞, а).

3. Если область замкнута и ее границам соответствуют значения аргумента а и b, то она будет описана элементарным неравенством вида (a<x)∙ (x<b). В стандартном виде эта запись будет выглядеть как .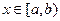

4. Области в векторе ответа будут расположены строго в направлении числовой оси. Поэтому преобразовывать в стандартную форму его можно чисто механически, сохраняя исходный порядок областей. Для объединения обозначений областей в одно выражение используется символ « ».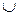

Пример 6

Требуется найти область определения функции:

.

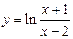Решение

Как известно, под областью определения функции понимают совокупность значений аргумента, при которых выражение, определяющее функцию, имеет смысл. Область определения заданной функции определяется из следующих условий:

· аргумент логарифма может принимать только положительные значения;

· знаменатель у дроби, стоящей под знаком логарифма не должен обращаться в ноль ( ).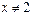

· числитель не должен обращаться в нуль ( ).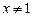

На начальном этапе можно решить неравенство:

.

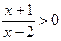А затем из полученной области исключить точки –1 и 2. Решение неравенства:

Что соответствует области: 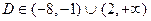. В исключении точек –1 и 2 нет необходимости, так как они не входят в означенную область.

Задания к лабораторной работе №11

Задание 1

Решить уравнения (по вариантам) численно и символьно.

№ варианта	Уравнение	Область определения	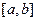№ варианта	Уравнение	Область определения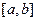
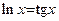		[3.5,4.5]		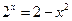	[0.5,0.8]
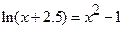	[-1.3,-0.7]		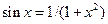[0.5,1]
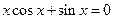	[1.8,2.2]		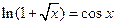[0.3,1.3]
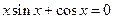		[2.7,2.9]		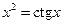	[0.5,1]
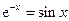	[0,0.6]		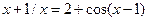[1.8,2.3]
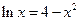	[1.5,2]		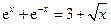[1,1.5]
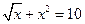		[2.6,3]		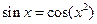	[0.7,1]
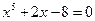	[1,1.5]		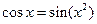[1.5,2]
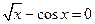	[0.5,0.7]		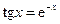[3,3.3]
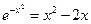		[-1,-0.5 ]		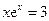	[1,1.5]
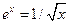	[0.3,0.8]		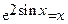[2.5,3]
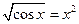	[0.5,1]		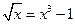[1,1.5]
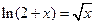		[1.4,2]		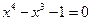	[-1,-0.5]
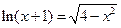	[1,2]		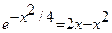[1.5,2]
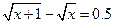	[0.2,1]		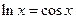[1,1.5]