Классическое определение вероятности. I. Расчет вероятности события 3

ОГЛАВЛЕНИЕ

I. Расчет вероятности события………………………………………3

II. Формула полной вероятности и формула Байеса………………..7

III. Схема Бернулли…………………………………………………….9

IV. Случайная величина……………………………………………….13

V. Элементы математической статистики…………………………..26

Контрольные задания:

Контрольная работа № 5……………………………………………..38

Контрольная работа № 6……………………………………………..45

Приложения:

Таблица 1. Значения функции стандартного распределе-

ния j(x)= 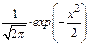……………………………………………51

Таблица 2. Значения нормированной функции Лапласа

F (x)= 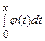………………………………………………………..52

Таблица 3. Значения функции 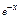…………………………………..53

Таблица 4. Значения коэффициентов Стьюдента t_γ = t(γ,n)………..54

Таблица 5. Значения параметра точности оценки стандарт-

ного отклонения нормальной случайной величины генераль-

ной совокупности q = q(γ,n)………………………………………….55

Учебное издание

Абуева Наталья Сергеевна

Макарова Ирина Леонидовна

Самарин Виктор Иванович

Якунина Наталья Федоровна

ТЕОРИЯ ВЕРОЯТНОСТЕЙ

И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА:

Методические указания по выполнению

Контрольных работ для студентов ЗФО

Экономических специальностей

Издательство СГУТиКД

354000, г. Сочи, ул. Советская, 26-а.

Тел./факс: 8(8622) 622-790

E-mail: [email protected]

http://surt.sochi.ru

Министерство образования и науки Российской Федерации

Сочинский государственный университет туризма и курортного дела

Н.С. Абуева, И.Л. Макарова,

В.И. Самарин, Н.Ф. Якунина

ТЕОРИЯ ВЕРОЯТНОСТЕЙ

И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА

Методические указания по выполнению

контрольных работ

Для студентов ЗФО экономических специальностей

Сочи – СГУТиКД

УДК 519.21

ББК 22.17я73

Представлено кафедрой прикладной математики ИИТиМ

Рекомендовано к печати Ученым советом Института информационных технологий и математики СГУТиКД

Абуева Н.С., Макарова И.Л., Самарин В.И., Якунина Н.Ф.

Теория вероятностей и математическая статистика: Методические указания по выполнению контрольных работ для студентов ЗФО экономических специальностей. – Сочи: СГУТиКД, 2004. –

56 с.

Указания содержат основные определения, правила, теоремы и формулы, необходимые для решения простейших задач по теории вероятностей и математической статистике, а также варианты контрольных заданий.

УДК 519.21

ББК 22.17я73

Лицензия ЛР № 022330 от 30.03.99. Авторская редакция.

Подписано в печать . . 2004. Формат 60х84/16. Бумага офсетная.

Гарнитура шрифта Таймс. Печать трафаретная. Уч.-изд. л. 3,2. Тираж 200 экз. Заказ №

Отпечатано с готового оригинал-макета.

г. Краснодар

© Н.С. Абуева, И.Л. Макарова, В.И. Самарин, Н.Ф. Якунина, 2004

© СГУТиКД, 2004

Таблица 5.

Значения ПАРАМЕТРА точности оценки стандартного отклонения

Нормальной случайной величины генеральной совокупности

q = q(γ,n)

(n – объем выборки, γ – доверительная вероятность)

γ n	γ = 0,95	γ = 0,99	γ = 0,999	γ n	γ = 0,95	γ = 0,99	γ = 0,999
	1,37	2,67	5,64		0,37	0,58	0,88
	1,09	2,01	3,88		0,32	0,49	0,73
	0,92	1,62	2,98		0,28	0,43	0,63
	0,80	1,38	2,42		0,26	0,38	0,56
	0,71	1,20	2,06		0,24	0,35	0,50
	0,65	1,08	1,80		0,22	0,32	0,46
	0,59	0,98	1,60		0,21	0,30	0,43
	0,55	0,90	1,45		0,188	0,269	0,38
	0,52	0,83	1,33		0,174	0,245	0,34
	0,48	0,78	1,23		0,161	0,226	0,31
	0,46	0,73	1,15		0,151	0,211	0,29
	0,44	0,70	1,07		0,143	0,198	0,27
	0,42	0,66	1,014		0,115	0,160	0,211
	0,40	0,63	0,96		0,099	0,136	0,185
	0,39	0,60	0,92		0,089	0,120	0,162

Примечание

Точность оценки стандартного отклонения нормальной случайной величины генеральной совокупности определяется значением s∙q, то есть, интервальная оценка (доверительный интервал) для стандартного отклонения определяется как s∙(1 – q) < σ₀ < s∙(1 + q), где s – исправленное выборочное стандартное отклонение. Поскольку по определению σ₀ неотрицательная величина, то в случае q > 1 интервальную оценку для стандартного отклонения σ₀ нормальной случайной величины генеральной совокупности следует определять как 0 < σ₀ < s∙(1 + q).

Таблица 4.

Значения коэффициентов стьюдента t_γ = t(γ,n)

(n – объем выборки, γ – доверительная вероятность)

γ n	γ = 0,8	γ = 0,9	γ = 0,95	γ = 0,98	γ = 0,99	γ = 0,999
	1,886	2,920	4,303	6,965	9,925	31,599
	1,638	2,353	3,182	4,541	5,841	12,924
	1,533	2,132	2,776	3,747	4,604	8,610
	1,476	2,015	2,571	3,365	5,032	6,859
	1,440	1,943	2,447	3,143	3,707	5,959
	1,415	1,895	2,365	2,998	3,499	5,405
	1,397	1,860	2,306	2,896	3,355	5,401
	1,383	1,833	2,262	2,821	3,250	4,781
	1,372	1,812	2,228	2,764	3,169	4,587
	1,363	1,796	2,201	2,718	3,106	4,437
	1,356	1,782	2,179	2,681	3,055	4,318
	1,350	1,771	2,160	2,650	3,012	4,221
	1,345	1,761	2,145	2,624	3,977	4,140
	1,341	1,753	2,131	2,602	2,947	4,073
	1,337	1,746	2,120	2,583	2,921	4,015
	1,333	1,740	2,110	2,567	2,898	3,965
	1,330	1,734	2,101	2,552	2,878	3,922
	1,328	1,729	2,093	2,539	2,861	3,883
	1,325	1,725	2,086	2,528	2,845	3,850
	1,323	1,721	2,080	2,518	2,831	3,819
	1,321	1,717	2,074	2,508	2,819	3,792
	1,319	1,714	2,069	2,500	2,807	3,767
	1,318	1,711	2,064	2,492	2,797	3,745
	1,316	1,708	2,060	2,485	2,787	3,725
	1,315	1,706	2,056	2,479	2,779	3,707
	1,314	1,703	2,052	2,473	2,771	3,690
	1,313	1,701	2,048	2,467	2,763	3,674
	1,311	1,699	2,045	2,462	2,756	3,659
	1,307	1,692	2,032	2,443	2,720	3,600
	1,304	1,685	2,023	2,426	2,708	3,558
	1,301	1,681	2,016	4,415	2,692	3,527
	1,299	1,677	2,009	4,405	2,679	3,502
	1,296	1,672	2,001	2,391	2,662	3,464
	1,294	1,668	1,996	2,383	2,649	3,439
	1,292	1,664	1,991	2,376	2,640	3,418
	1,291	1,662	1,987	2,370	2,633	3,403
	1,290	1,660	1,984	2,365	2,627	3,392
	1,289	1,658	1,980	2,358	2,617	3,374
	1,288	1,656	1,976	2,353	2,609	3,357
	1,286	1,653	1,972	2,345	2,601	3,340
	1,283	1,648	1,965	2,334	2,586	3,310
∞	1,282	1,645	1,960	2,326	2,576	3,291

I. Расчет вероятности события

Классическое определение вероятности

При классическом определении вероятность события определяется равенством

р(A)= 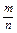, (1)

где m – число исходов проводимого опыта, благоприятствующих появлению события А; n – общее число возможных исходов.