Второй закон термодинамики для необратимых процессов

Уравнения первого закона термодинамики для необратимых и обратимых процессов имеют вид

δQ_(необр) = dU + δA_(необр) (2.22)

и

δQ_(обр) = dU + δA_(обр) (2.23)

Вычитая уравнение (2.23) из уравнения (2.22), получим для кругового процесса

δQ_(необр) – δQ_(обр) = δА_(необр) – δА_(обр). (2.24)

Если бы оба процесса были обратимы, то уравнение (2.24) было бы равно нулю. Поскольку это не так, возможны следующие соотношения:

δQ_(необр) > δQ_(обр) и δА_(необр) > δА_(обр) (2.25)

и

δQ_(необр) < δQ_(обр) и δА_(необр) < δА_(обр) (2.26)

Из соотношения (2.25) следует, что в результате кругового процесса вся теплота, полученная системой, превращается в работу и это является единственным результатом процесса, что противоречит второму закону термодинамики. Значит, соотношение (2.25) невозможно. Поэтому единственно правильным будет соотношение (2.26). Из него следует, что работа любого необратимого процесса при прочих равных условиях всегда меньше работы обратимого процесса. Поэтому работу обратимых процессов называют максимальной работой.

δА_(обр) = δА_(макс) или А_(обр) = А_(макс) (2.27)

Чем меньше работа процесса, по сравнению с максимальной работой, тем более процесс является необратимым.

Из уравнения ( 2.26) следует, что

δQ_(необр) < δQ_(обр) (2.28)

Тогда после подстановки δQ_(необр) в уравнение (2.16) получим:

dS > 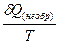и ТdS > δQ_(необр (2.29)

Уравнение (2.29) представляет собой математическую формулировку второго закона термодинамики для необратимых процессов.

Для изолированных систем уравнение (2.29) примет вид:

dS > 0 и ΔS > 0 (2.30)

Для процессов, протекающих при Т = cоnst справедливо соотношение:

ΔS > 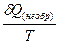или TΔS = Q_(необр) (2.31)

Таким образом, второй закон термодинамики для необратимых процессов выступает, как закон существования и возрастания энтропии в изолированных системах при протекании в них необратимых процессов.

Объединяя уравнения (2.16) и (2.29), получим:

dS ≥ 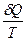(2.32)

или

ТdS ≥ δQ (2.33)

Где знак > относится к необратимым (самопроизвольным) процессам, а знак = относится к обратимым (равновесным) процессам, к условиям равновесия в системе.

Уравнения (2.32) и (2.33) представляют собой математическую формулировку второго закона термодинамики в общем случае.

Поставляя в уравнение первого закона термодинамики вместо δQ значение (2.33), получим объёдинённое уравнение первого и второго законов термодинамики:

TdS ≥ dU + δA (2.34)

или

TdS ≥ C_VdT + PdV (2.35)

Уравнения (2.34) и (2.35) часто называют основным уравнениями химической термодинамики.

Энтропия может служить критерием возможности протекания процесса и состояния равновесия в изолированной системе. Согласно уравнения (2.30) в изолированной системе самопроизвольные необратимые процессы протекают с увеличением энтропии. По мере протекания процесса энтропия системы будет возрастать. Поскольку любой процесс прекращается, когда в системе устанавливается равновесие, то, очевидно, что равновесие в системе установится, тогда, когда энтропия системы достигнет максимального значения. В изолированной системе объём и внутренняя энергия постоянны. Поэтому математически условие максимума энтропии, а, следовательно, условие равновесия в изолированной системе описывается уравнениями:

(dS)_V,U = 0 и (d²S)_V,U < 0 (2.36)