Лапластың локальдық және интегралдық теоремасы».

Лапластың локальдық теоремасы.

Лапластың локальдық теоремасы, егер тәжірибелер саны жеткілікті көп болса, n тәжірибелерде оқиғалардың дәл k рет болатындығының ықтималдығын жуықтап есептеуге мүмкіндік береді.

Лапластың локальдық теоремасы. Егер әр тәжірибеде А оқиғасы болатындығының р ықтималдығы тұрақты және ноль мен бірден айырмашылығы болса, n тәуелсіз тәжірибелерінде А оқиғасы дәл k рет болатынның 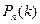ықтималдығы (қаншалықты n көп болса, соншалықты дәлірек) мынаған тең :

,

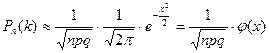мұндағы

, .

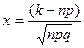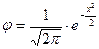x – тің оң мәндері үшін 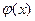функциясының кестесі 1-қосымшада; теріс мәндері үшін де осы кестені пайдалануға болады, себебі 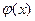функциясы - жұп, .

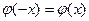Мысалы,

152 тәжірибеде А оқиғасының 50 рет болуының ықтималдығын табыңыз, егер осы оқиғаның әр тәжірибеде болуының ықтималдығы 0,25-ке тең болса

Шешуі: Шарт бойынша: n=152, k=50, p=0,25, q=0,75.

n=152 жеткілікті үлкен сан болғандықтан, Лапластың локальдық теоремасын қолданайық:

,

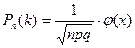мұнда

.

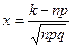Есептейміз

.

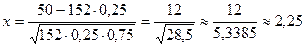1 қосымшадағы кесте бойынша .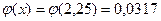

Ізделінді ықтималдық:

.

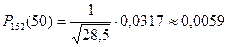Лапластың интегралдық теоремасы.

Лапластың интегралдық теоремасы. n тәуелсіз тәжірибелерінде, олардың әрқайсысындағы оқиғаның көрінуінің ықтималдығы p (0<p<1), оқиға 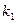-дан аз емес және 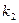-дан көп емес рет пайда болатындығының ықтималдығы шамамен мынаған тең:

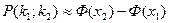, мұндағы ,

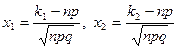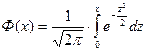- Лаплас функциясы

Оң мәндер үшін Лаплас функциясының кестесі 2-ші қосымшада берілген, теріс мәндері үшін де осы кестені қолдануға болады, себебі Лаплас функциясы тақ:

.

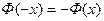Мысалы,

Бөлшектің тексерістен өтпегендігнің ықтималдығы p=0,2 –ге тең. 400 кездейсоқ алынған бөлшектердің 70 пен 100 аралығында тексерілмеген болатындығының ықтималдығын тап.

Шешуі: Шарт бойынша, p=0,2, q=0,8, n=400, 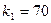, 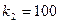. Лапластың интегралдық теоремасын пайдаланайық:

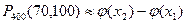
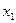және 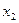- ні есептеп шығарайық.

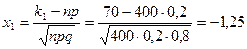
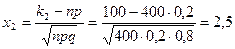
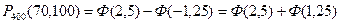
2-ші қосымшадағы кесте бойынша мынаны табамыз:

.

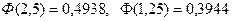Ізделінді ықтималдық

.

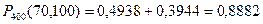Салыстырмалы 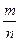жиеліктің тұрақты р ықтималдығынан абсолюттік шамасы бойынша берілген 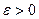санынан аспайтындығының ықтималдығын табу мақсатын алға қояйық. Басқаша айта келсек, теңсіздікті орындау ықтималдығын табайық.

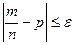
бұл ықтималдық мына формула бойынша табылады

.

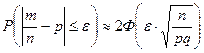Дәріс №4.

Тақырыбы: «Кездейсоқ шамалар. Кездейсоқ шамалардың үлестірім заңы. Дискретті кездейсоқ шамалар».

Кездейсоқ деп – тәжірибе қорытындысында қандай да бір мүмкін болатын мәндер қабылдай алатын айнымалыны атайды.

Кездейсоқ шамаларды X, Y, Z,… және басқа да бас әріптерімен, ал олардың қабылдайтын мәндерін сәйкесінше кіші әріптермен белгілейміз.

Дискретті шамалардың екі түрі болады: дискретті және үздіксіз.

Дискретті кездейсоқ шамалар: бұл кездейсоқ шамалардың мәндерінің бір бірінен айырмашылығы - қандай да бір соңғы шамада. Қабылдайтын мәндерінің саны ақырлы немесе есепті болса, Х кездейсоқ шамасы дискретті деп аталады.