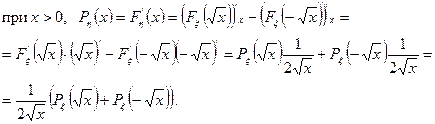Функции от случайной величины.

Определение. Множество точек на числовой прямой R называется борелевским если оно может быть получено из множеств вида 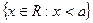применением конечного или счётного числа операций объединения, пересечения и дополнения.

Класс борелевских множеств достаточно широк. В нём содержатся множества вида: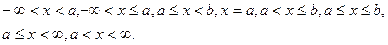

Практически все встречающиеся в приложениях числовые множества являются борелевскими.

Пусть (Ω, S, P) произвольная вероятностная схема (связанная с некоторым опытом) и 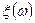- случайная величина. Рассмотрим числовую функцию 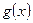. Подставляя вместо х случайную величину ξ, мы получим новую случайную величину .

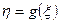На функцию 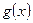наложим ограничение: для любого борелевского множества В множество 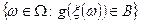является событием, т.е. принадлежит S.

К множеству таких функций принадлежат, в частности, непрерывные и кусочно непрерывные функции (непрерывные функции на числовой прямой за исключением конечного числа точек разрыва 1-го рода). В дальнейшем мы такие функции и будем рассматривать.

Рассмотрим пример, когда случайная величина есть ДСВ или НСВ.

Пример 1. Пусть ξ есть ДСВ и 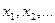- возможные значения ξ , а 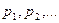- их вероятности. Тогда множество значений случайной величины 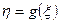будет состоять из множества чисел 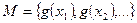. Среди этих чисел могут быть совпадающие. Подсчитаем теперь вероятности различных значений величины η.

Пусть 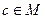, тогда событие 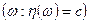есть сумма несовместных событий вида 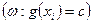и, значит:

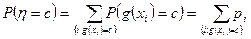(1)

Итак, чтобы найти вероятность события 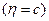, нужно из всех возможных значений 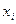величины ξ выбрать те, для которых 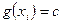и просуммировать их вероятности.

Пример 1. Пусть закон распределения величины ξ имеет вид:

Значение	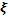-2	-1
Вероятности	0,1	0,2	0,3	0,05	0,15	0,2

Найдём закон распределения случайной величины .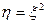

Возможные значения η будут: 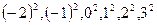т.е. 0,1,4,9. Их вероятности будут равны:

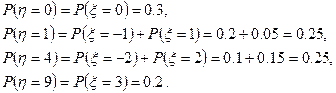
Следовательно, закон распределения для η будет:

Значение η
Вероятности	0,3	0,25	0,25	0,2

Рассмотрим ещё два примера вычисления функции распределения 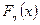и плотности 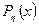случайной величины 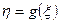по функции распределения 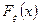и плотности .

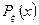Пример 2. Пусть функция 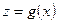монотонно возрастает. Тогда у неё существует обратная функция 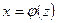, такая, что 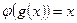. Тогда, если 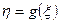, имеем:

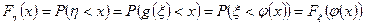(2)

Дифференцируя (2) по х, имеем (в предположении, что 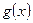дифференцируема и имеется плотность 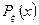), используя производную для сложной функции:

= ,

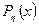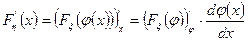откуда получаем (используя производную для обратной функции) соотношение между плотностями

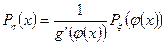. (3)

В частности, при 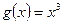имеем 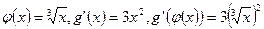и значит плотность распределения случайной величины 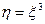имеет вид

.

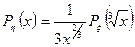Пример 3. Пусть 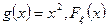– непрерывная функция распределения с плотностью .

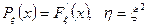В данном случае функция 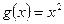не является монотонной и, поэтому, нельзя применить формулу (3).

Вычислим 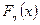непосредственно, исходя из её определения.

При 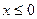имеем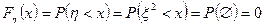

При 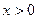получаем

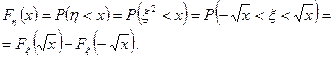
Беря производную от левой и правой частей, получаем, используя формулу для производной сложной функции:

при 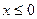,
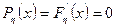