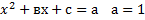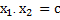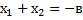Способ для определения четной или не четной функции

В формуле функции в место (х)подставляем»-х».

а .Если функция остается такая же, то она четная.

б.Если функция полностью меняет знак, то онанечетная .

в. Если знак меняется частично ,то ни то, ни её.

Алгоритм.Решение неравенств методом интегралов(метод»Несси»)

1)

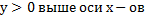
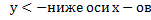
2)Найти нули функции

3)Делаем рисунок Несси(хвост всегда чертить над водой рисуем справа сверху)

Несси »ныряет « через нули функции.

4)Записываем ответ в виде числовых промежутков.

Алгоритм. Нахождение производной по формуле

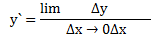
1)Нахождение превращение функции

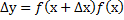
2.Разделить на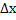

3.Привести к приделу.

Формулы производной

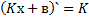
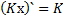
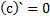
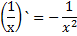
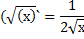
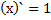
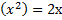
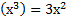
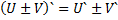
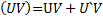
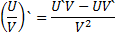
3 вида задач на %

1.Что найти % от числа надо это число умножить столько сотых столько %

2.Чтобы найти всё количество, надо это число разделить на столько сотых столько %

3.Чтобы найти процентное отношение, надо меньшее число разделить на все количество сколько получится сотых столько будет процентов.

Алгоритм. Исследования функции для построение графиков.

1)Область определения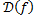

2)Множество значении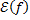

3)Периодичность Т-период

4)Точка пересечения с осями координат

а)с осями у: х=0

б)с осями х: у=0

5)Четность или нечётность

6)Возрастание или убывание

7)Экстремумы( min и max)

8)Промежуток знакопостоянства (над водой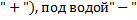

9)Асимптоты

Тригонометрические формулы.

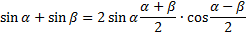
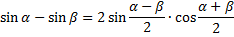
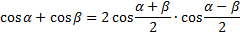
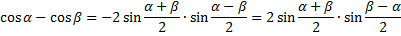
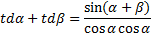
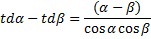
Физический смысл производной -это мгновенная скорость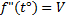

Уравнение касательной

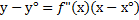
Алгоритм

1)Дано: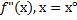

2)Вычислить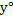

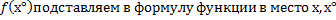
3)Найти: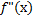

4)Найти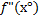

5)Применяем формулу

Производная сложной функции

Алгоритм

1.Бёрем производную как от простой функции.

2.Умножаем на производную сложного аргумента

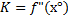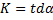Геометрический смысл производной –это угловой коэффициент касательной тангенса угла наклона касательной.

Алгоритм. Исследование функции с помощью производной.

1)Найти область определения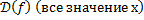

2)Найти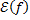

3)Чётность или нечётность

4)Точки пересечения графика с осями координат

Х=0(с осью У)

У=0(с осью Х)

(Нули функции)

5)Промежутки знакопостоянства

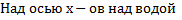(Под осью х-ов под водой)

6)Участки возрастания и убывания

7)Экстремумы

8)Асимптота

9)Дополнительные точки

10)Построение графика

1)Переодичность (у т.ф)

Алгоритм. Нахождение наибольших значении функции но отрезке а,в

min

1.Найти все max и всеmin

2.Найти значения функции на концах отрезки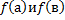

3.Выбрать из них самое большое число и самое меньшое

Замечание для более сложных случаев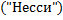

1.Записать О.Д.З.

2.х всегда 1 месте

3.Знаменятель поднимаем вверх

4.Ныряем через нули только в нечётной степени

5.Выражения типа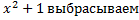

x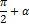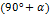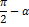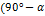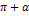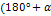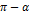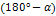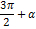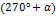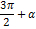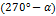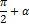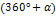

)

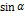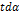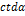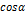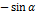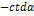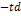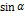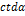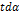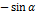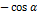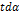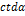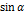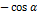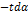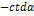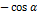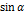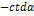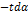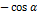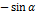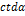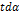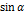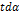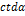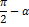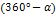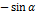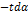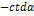Некоторые значения тригонометрических функции

Угол	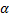Значение угла в радианах(градусах)
функции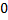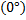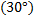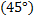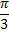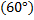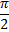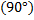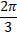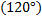
					-
	-

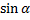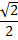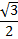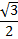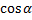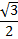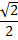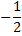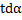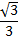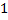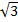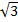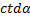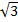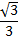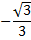Площадь плоских фигур

1)Треугольник:

Прямоугольный треугольник,а,в –катеты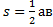

Равнобедренный треугольник а-основание в- боковые стороны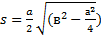

Произвольный треугольник: а,в,с-стороны; h-высота;

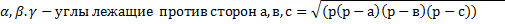
гдеR-радиус описанной окружности ,r-вписанной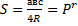

Равносторонний треугольник а- сторона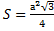

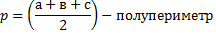
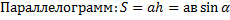
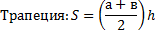
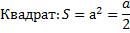
Прямоугольник: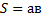

Ромб: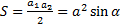

Любой четырехуголик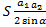

Круг: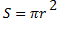

Сектор: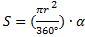

Теорема Виета

(только для приведенных квадратных уравнении)