Тепловые напряжения и тепловых деформации в машинах

Глава 8

Повышенные температуры наблюдаются не только в тепловых машинах, у которых нагрев является следствием рабочих процессов. В «холодных» машинах нагреваются механизмы, работающие при высоких скоростях и больших нагрузках (зубчатые передачи, подшипники, кулачковые механизмы и т. д.). Детали, подверженные циклическим нагрузкам, греются в результате упругого гистерезиса при многократно повторных циклах нагружения-разгружения, а также за счёт выделения тепла в узлах трения (подшипниковые узлы, червячные передачи, …). Повышение температуры сопровождается изменением линейных размеров деталей и может вызвать высокие напряжения.

Если материал при колебаниях температуры лишен возможности свободно расширяться или сжиматься, то в нем возникают тепловые напряжения.

Различают торможение тепловых деформаций детали сопряженными деталями (торможение смежности), которое зачастую возникает при выборке зазоров в узлах и торможение деформаций волокон детали смежными волокнами (торможение формы), которое возникает в самой детали при невозможности изменить геометрические размеры при нагревании или охлаждении.[36]

Торможение смежности. Одним из примеров торможения смежности является соединение деталей, имеющих при работе различную температуру или выполненных из материалов с неодинаковыми коэффициентами линейного расширения.

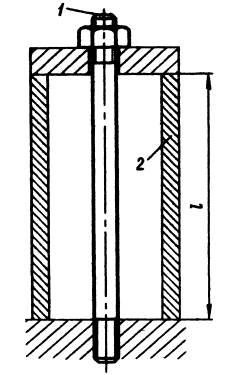Пусть болт 1 и втулка 2 (рис. 8.1) изготовлены из материала с коэффициентами линейного расширения а₁ и а₂ и их температуры равны соответственно t₁ и t₂. При нагреве от исходной температуры t₀ болт и втулка в свободном состоянии удлинились бы на величины соответственно la₁∆t₁ и la₂∆t ₂ , где ∆t₁ = t₁ — t₀; ∆t ₂ = t₂ — t₀; l — длина соединения. В стянутой системе образуется температурный натяг

f₁ = la₂∆t ₂ - la₁∆t_1, (8.1)

или в относительных единицах

e₁ = a₂∆t ₂ - a₁∆t_{1 .} (8.2)

В соединении возникает термическая сила Р_T вы­зывающая по закону Гука относительное удлинение болта e₁ = 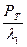и укорочение втулки 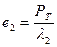, где

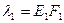и 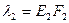- коэффициенты жесткости соответственно болта и втулки (F₁ и F₂ — сечения болта и втулки). Сумма относительных деформаций 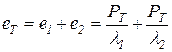. Откуда

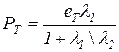. (8.3)

Рис. 8.1. Схема торможения смежности

Примем, что температура стягивающей и стягиваемой деталей оди­накова (как это обычно и бывает в машинах при установившемся тепло­вом режиме). Полагая t_t — t₂ — t, получаем из формул (8.2) и (8.3) 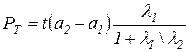. (8.4)

Возможны три случая:

1. а₂ > а₁ (стяжка деталей из алюминиевых, магниевых и медных сплавов стальными болтами и болтами из титановых сплавов). При нагреве в таких соединениях возникает натяг, пропорцио­нальный фактору t (а₂ — а₁). При охлаждении до минусовых температур этот фактор становится отрицательным. Следовательно, первоначальный сборочный натяг уменьшается, т. е. соединение ухудшается.

2. а₁ > а₂ (стяжка стальных и чугунных деталей болтами из аустенитных сталей; стяжка деталей из титановых сплавов стальными болтами). При нагреве фактор t(а₂—а₁) отрицателен, т. е. соединение ухудшается, а при охлаждении до минусовых температур положителен, т. е. перво­начальный натяг увеличивается.

3. а₁ = а₂ (стяжка стальных и чугунных деталей стальными болтами; стяжка деталей из титановых сплавов титановыми болтами). В этом случае

t (а₂ — а₁) = 0, т. е. первоначальный натяг при нагреве и охлаждении не меняется.

Иллюстрация этих закономерностей приведена на рис. 8.2, изобража­ющем изменение температурного натяга t (a₂ — а₁) при стяжке корпусов из различных материалов стальными (8.2, а) и титановыми (8.2, б) бол­тами. Значения а₂ и а₁ взяты из рис. 8.3.

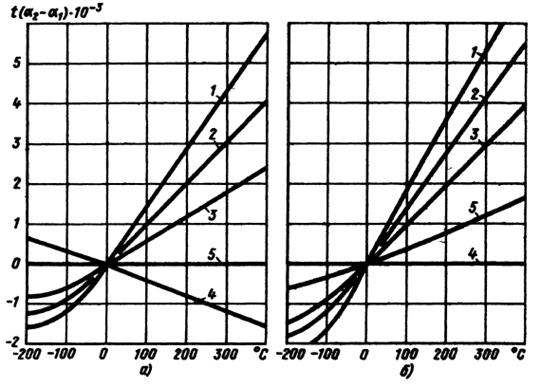
Рис. 8.2

Термический натяг при стяжке корпусов стальными (а) болтами и титановыми (б) болтами.

Материалы корпусов:

1- сплавы Mq,

2- сплавы Аl,

3 – бронзы,

4- сталь и чугун

Согласно формуле (8.3) напряжение растяжения в болте

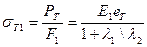. (8.5)

Напряжение сжатия во втулке 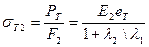. (8.6)

Отношение 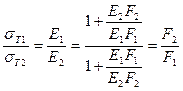. (8.7)

не зависит от модулей упругости материалов шпильки и втулки и опре­деляется только соотношением сечений последних.

На рис. 8.4 приведены подсчитанные по формулам (8.5) и (8.6) напряжения 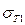и 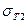в функции 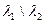для стальных шпилек и корпусов из различных материалов (принято е_Т = 1; Е₁ = 1; величины Е₂ выражены в долях от Е₁).

Термические напряжения в шпильках резко падают с увеличением 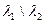(жесткие шпильки, упругие корпуса). Напряжения в корпусах наоборот возрастают, но при обычных значениях 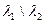< 1 и для обычных литейных материалов (чугун, легкие сплавы) имеют значительно меньшую величину, чем в шпильках.

На основании графика и формул (8.5), (8.6) можно сделать следующие выводы:

для уменьшения термических напряжений в шпильках корпус сле­дует делать упругим, а шпильки - жесткими;

для уменьшения термических напряжений в корпусе шпильки следует выполнять упругими, а корпус - жестким.

Рис. 8.3.

Коэффициент линейного расширения в функции температуры:

1 — сплавы Ti;

2 — стали мартенситного класса;

3 — стали перлитного класса ичугуны;

4 - стали аустенитного класса;

5 - бронзы;

6 - латуни;

7 - сплавы А1;

8 - сплавы Mg

Прочность корпуса обычно не является определяющей для прочности стяжных соединений, поэтому для термически нагруженных соединений целесообразно придерживаться правила: упругий корпус — жесткие шпильки.

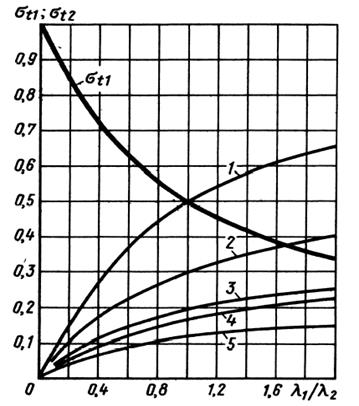
Рис. 8.4.

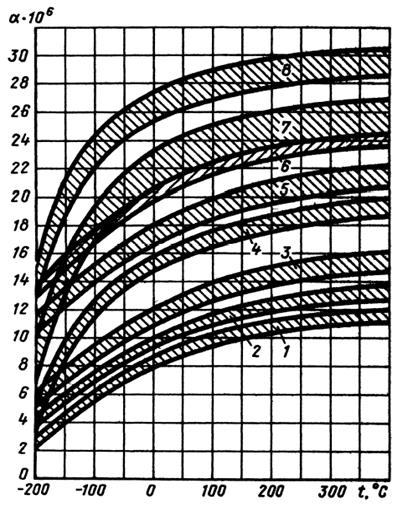
Относительные термические напряжения 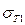(жирная линия)

и 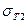(тонкие линии)

в функции .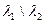

Материалы корпусов:

1 — сталь;

2 — сплавы Ti;

3 — чугуны;

4 — сплавы А1;

5 - сплавы Mg

Прочность стяжных соединений помимо термических напряжений в значительной степени зависит от силы предварительной затяжки соеди­нения и рабочих сил, действующих на соединение.

Из уравнения (8.3) следует, что возможны следующие способы умень­шения термической силы:

- уменьшение разности температур сопряженных деталей (например, охлаждением стягиваемой детали или увеличением температуры стягива­ющей детали);

- уменьшение разницы в величинах коэффициентов линейного расшире­ния (соответствующим подбором материалов сопряженных деталей).

Если материалы стягивающей и стягиваемой деталей заданы, то тер­мическую силу можно уменьшить введением между стягивающей и стягиваемой деталями промежуточных втулок 1 (рис. 8.5, а), выполненных из материалов с малым коэффициентом линейного расширения, например инвара.

Инвар (36Н) представляет собой железоникелевый сплав (36% Ni, остальное Fe). Коэф­фициент линейного расширения в интервале температур от 0 до 100°С равен

(0 - 1,5) 10 ^-61/°С, резко повышается при t > 200°С . Еще более низким коэффициентом линейного расширения [а= (0 -0,5)*10 ^-6 1/°С в интервале 0-100°С] обладает суперинвар Н30К4Д 32% Ni, 4% Со, 0,7% Си, остальное Fe).

В этом случае температурный натяг f₁ = l₂ a₂ t₂ + l₃ a₃ t₃ – l₁ a₁ t₁, (8.8)

где а₂, а₃, а₁ - коэффициенты линейного расширения соответственно стягиваемых деталей, втулки и шпильки; t₂, t₃, t₁ и l₂, l₃, l₁ — соответственно их температуры и длины.

Вводя l₃ = l₁ – l₂ полагая t₂ = t₃ = t₁ и приравнивая выражение (8.8) нулю, получаем условие отсутствия температурного натяга:

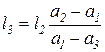. (8.9)

Подставляя a₂ = 22*10^-6 (алюминиевый сплав), a₃= 1.5*10^-6 (инвар при

20-150 ⁰C) и a₁ = 11 * 10^-6(сталь), находим l₃= 1.15l₂ (8.10)

т. е. для полной ликвидации температурного натяга длина инварной втулки должна превышать на 15% длину стягиваемых деталей. Конструк­тивно это трудно выполнимо.

Есть материалы, коэффициент линейного расширения которых близок к нулю в широком интервале температур (например, кварц а = 0,55 * 10^-6) и даже имеет отрицательную величину (т. е. размеры детали с нагревом уменьшаются). К таким материалам относятся некоторые ситаллы (а = - 5 * 10 ^-6). Расчет по формуле (8.9) дает в этом случае l₃ = 0,7l₂. Даже при таких условиях промежуточная втулка должна иметь значи­тельную длину.

Для уменьшения термических напряжений стяжные болты иногда выполняют из материалов с высоким коэффициентом линейного расши­рения, например из хромоникелевых аустенитных сталей, для которых a = (14 - 18) * 10 ^-61/°С.

Рис. 8.5. Уменьшение термических напряжений в стяжных соединениях

Действенным средством уменьшения термических напряжений является установка пружинных элементов на корпусах или, что конструктивно удобнее, на болтах (см. рис. 8.5, б). Согласно формуле (8.3) установка пружинных элементов на болтах снижает термическую силу в отношении

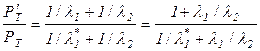, (8.11)

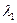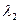где и — коэффициенты жесткости соответственно болта и стягивае­мых деталей; 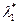— коэффициент жесткости болта с упругим элементом

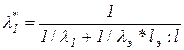, (8.12)

где 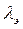— коэффициент жесткости упругого элемента; l_э и l — длины соответственно упругого элемента и болта.

Из формулы (8.11) следует, что термическая сила снижается тем больше, чем выше упругость элемента (чем меньше ).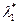

Если, например, 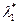= 0,1 и 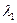/ 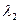=0,5, то ,

т.е. термическая сила уменьшается в 7 раз. При достаточно большой упругости элемента термические силы могут быть практически полностью погашены.

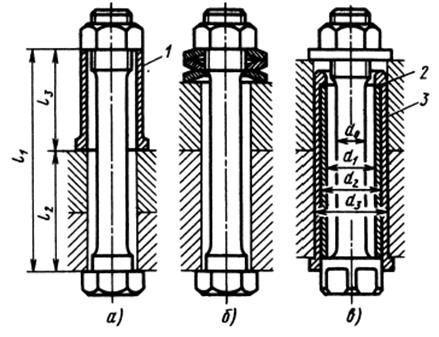
При ограниченных осевых размерах болт устанавливают в концентрич­ных втулках 2, 3 (см. рис. 8.3, в), из которых первая при затяжке болта работает на сжатие, а вторая — на растяжение. Если сечения болта и втулок равны

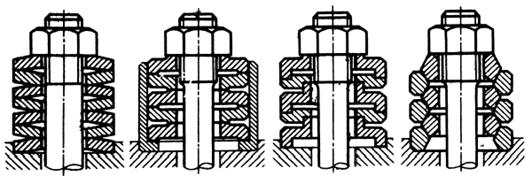(d₂ = 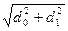; d₃ = 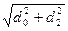),то упругость системы повышается приблизительно в 3 раза по сравнению с упругостью собственно болта. Упругие элементы часто применяют для поглощения термических деформаций при установке на валу нескольких деталей, выполненных из сплавов с повышенным коэффициентом линейного расширения (например, роторов многоступенчатых аксиальных компрессоров). Для фиксации и затяжки таких деталей требуется значительная осевая сила. Поэтому упругие элементы в данном случае выполняют в виде набора много­численных прочных и относительно жестких элементов (рис. 8.6), в сумме дающих необходимую упругость.

Рис. 8.6. Упругие элементы в системах силовой затяжки

Торможение формы.

Тепловые напряжения, вызванные торможением формы, возникают при неравномерном нагреве детали, когда отдельные волокна материала лишены возможности по конфигурации детали рас­ширяться в соответствии с законом тепловой деформации. В отличие от торможения смежности здесь напряжения возникают только при пере­паде температуре в теле детали (при стационарном тепловом потоке, когда тепло переходит от горячих участков к более холодным, или при неустановившемся тепловом потоке, например при тепловом ударе, когда волна тепла распространяется по телу детали).

Как общее правило, горячие участки детали с температурой, превышающей среднюю, испытывают напряжения сжатия, а более холодные — напряжения растяжения. Это же справедливо при минусовых температурах: менее холодные участки подвергаются - сжатию, а более холодные - растяжению, Тело, имеющее во всех своих частях одинаковую темпера­туру, термических напряжений не ис­пытывает.

Плоские стенки.

Представим себе плоскую стенку толщиной s (рис. 8.7, а), через которую в направлении, перпендикулярном ее плоскости, проходит равномерный тепловой поток. Пусть поверхность стенки, обращенная к источнику теплоты, имеет температуру t₁, а противоположная поверх­ность t₂, причем

t₁ >t₂. Температура поперек стенки, как известно из теории теплопередачи, изменяется по прямолинейному закону.

Средняя температура стенки t_cp = 0,5 (t_l + t₂).

Мысленно рассечем пластинку на ряд тонких параллельных слоев. Если бы всеони имели возможность свободно расширяться под действием температуры, то слои с температурой выше t_cp удлинились бы по сравнению со средним слоем, а слои с температурой ниже t_cp приобрели бы размеры меньше размеров среднего слоя, и пластинка приняла бы форму, изображенную на рис. 8.7, б.

Рис. 8.7. К определению термических напряжений

Относительное удлинение крайнего, наиболее нагретого слоя

e₁ = a (t₁ - t_cp) = 0,5 (t₁ - t₂). (8.13)

Относительное укорочение крайнего, наиболее холодного слоя

e₂ = a(t_cp -t₂) = 0,5a(t₁ - t₂), (8.14)

т.е. e₂ = e₁=e_max = 0,5(t₁ - t₂). (8.15)

Если пластинка сохраняет при нагреве плоскую форму, то все слои всилу совместности деформации должны иметь одинаковые размеры, равные размерам среднего слоя. В такой пластинке наиболее нагретые слои сжаты тормозящим действием смежных более холодных слоев, а наиболее холодные — растянуты действием более горячих слоев (рис. 8.7, в), каждый по двум взаимно перпендикулярным направлениям. Наибольшие напряжения возникают в крайних, поверхностных слоях.

Как известно из теории упругости, относительное удлинение при двух­осном напряженном состоянии

по оси х 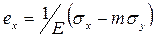, (8.16)

по оси y 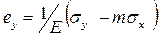, (8.17)

где 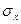и 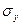— напряжения соответственно по осям х и у; m — коэффициент поперечной деформации — отношение величины поперечного сжатия к про­дольному удлинению в пределах упругих деформаций в случае простого растяжения в одном направлении.

При симметричном растяжении-сжатии (как в рассматриваемом случае)

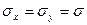; е_х — е_у = е. Следовательно, .

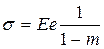Подставляя в это выражение величину е из уравнения (8.15), получаем максимальное значение напряжений в крайних слоях

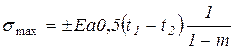(8.18)

где знак плюс относится к растяжению, а минус — к сжатию.

Напряжения поперек стенки изменяются, как и температура, по прямо­линейному закону. Перепад температур можно выразить через количество теплоты Q, проходящей через стенку в единицу времени на единицу поверхности. По закону Фурье 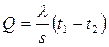, (8.19)

где 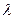— коэффициент теплопроводности материала, ккал/(м*ч*°С); s — толщина стенки, м.

Подставляя значение t₁ - t₂ из формулы (8.19) в уравнение (8.16),

получаем 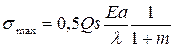. (8.20)

Тепловая прочность материалов.

Из формулы (8.18) следует, что макси­мальные термические напряжения, при заданной интенсивности теплового

потока Q пропорциональны толщине стенки s и фактору 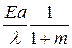, характерному для каждого материала (табл. 8.1).

Таблица 8.1. Тепловая прочность материалов

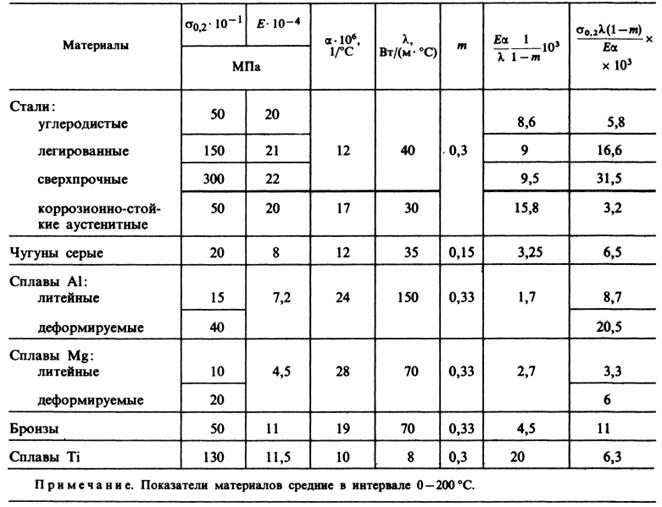
Фактор 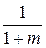для всех материалов близок к 1,5, за исключением чугунов, для которых он равен 1,18. Для всех остальных материалов можно пользоваться упрощенным выражением .

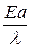Тепловая прочность, т. е. сопротивляемость материала действию тер­мических напряжений, характеризуется отношением предела текучести материала 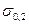к фактору 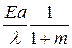(аналогичным запасу прочности): 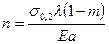. (8.21) Значения этого фактора приведены в табл. 8.1 и на рис. 8.8.

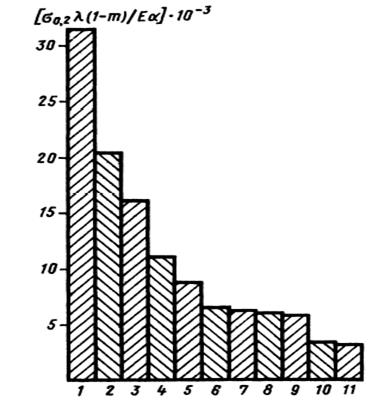
Рис. 8.8.

Тепловая прочность:

1 — стали сверхпрочные;

2 — сплавы Аl деформируемые;

3 — стали легированные;

4 - бронзы;

5 — сплавы Аl литейные;

6 — чугуны серые;

7 — сплавы Ti;

8 — сплавы Mg деформируемые;

9 — стали углеродистые;

10 - сплавы Mg литейные;

11 - стали корро­зионно-стойкие аустенитные

На первом месте по сопротивляемости термическим напряжениям (высокое значение фактора) стоят сверхпрочные стали, за ними деформи­руемые сплавы Аl. Наименее выгодны сплавы Mg и коррозионностойкие стали аустенитного класса.

Приведенные выше соотношения справедливы при температурах при­мерно до 200°С, когда показатели прочности, упругости, линейного рас­ширения и теплопроводности обычных конструкционных материалов из­меняются сравнительно мало. При переходе в область более высоких температур на первый план выступают жаропрочность, т. е. спо­собность длительно выдерживать напряжения в условиях высоких температур, и жаростойкость, т. е. способность сопротивлять­ся горячей коррозии. К жаропрочным мате­риалам относятся стали, легированные Ni, W, Mo, Ti, Nb, сплавы на никелевой основе, титановые сплавы и др. В области высоких температур качественные соотношения между материалами становятся иными. С повыше­нием температуры большинство рассмотренных выше материалов (например, стали обычного состава) теряет прочность; некоторые из них вообще не способны выдерживать высокие температуры (легкие сплавы). Титановые сплавы, которые в условиях умеренных температур имеют посредственную тепловую прочность, здесь выдвигаются на одно из первых мест.

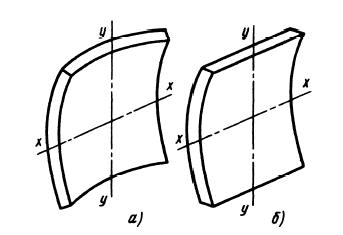Криволинейные стенки. В предшествующих рассуждениях предполага­лось, что пластинка при термических деформациях сохраняет плоскую форму, т. е. или она расположена в жестких направляющих, или доста­точно жестка против действия изгиба. Если пластинка свободно дефор­мируется под действием перепада температур, то термические напряжения уменьшаются и при известных условиях могут практически исчезнуть, если пластинка достаточно тонка, сделана из материала с малым модулем упругости и может изогнуться настолько, что наружные волокна ее удлинятся, а внутренние укоротятся на величину a ( t₁ —t₂).

Рис. 8.9. Изгиб пластинки под действием термических напряжений

Пластинка при этом изгибается по сферической поверхности (рис. 8.9, а), средний радиус которой .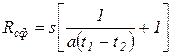

Если свободный изгиб возможен только в одном направлении, то пластинка изгибается по цилиндру (рис. 8.9, б), средний радиус которого

.

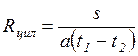Полые цилиндрические детали.На практике встречаются случаи, когда при перепаде температур форма детали в силу ее конфигурации не меняется или меняется незначительно. Типичным примером является цилиндрическая труба большой длины.

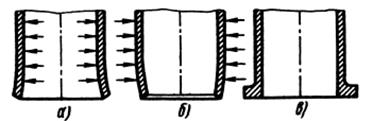
Рис. 8.10. Деформация свободного конца цилиндра

При одностороннем нагреве, на­пример изнутри (рис. 8.10, а) труба, расширяясь в радиальном и осевом направлениях, сохраняет в целом цилиндрическую форму. Внутренние, наиболее нагретые слои стенки при этом испытывают напряжения сжатия, а наружные, более холодные — напряжения растяжения. Напряжения па­дают только на свободном торце трубы, где сдерживающее влияние кольцевых сечений ослабевает, вследствие чего труба воронкообразно расширяется.

При нагреве снаружи (рис.8.10,6) картина обратная: наружные, более горячие слои подвергаются сжатию, внутренние — растяжению; свободные торцы трубы сходятся к центру.

Если необходимо сохранить правильную цилиндрическую форму, то следует вводить на торцах кольцевые ребра жесткости (рис. 8.10, в).

Сложение тепловых и рабочих напряжений.

Обычно термические напря­жения сочетаются с напряжениями от внешних нагрузок. Сочетание может быть благоприятным, если сложение термических и рабочих напряжений уменьшает результирующие напряжения, и неблагоприятным, если оно увеличивает последние. Это зависит от соотношения величин термических и рабочих напряжений и закономерности их изменения поперек стенки.

Тепловые деформации

В узлах, состоящих из деталей, имеющих различную рабочую температуру или изготовленных из материалов с разными коэффициентами линейного расширения, тепловые деформации могут существенно влиять на взаимное расположение деталей.

Осевые зазоры. При нагреве в сочленениях возникают термические зазоры или натяги, которые необходимо учитывать при назначении сборочных (холодных) зазоров.

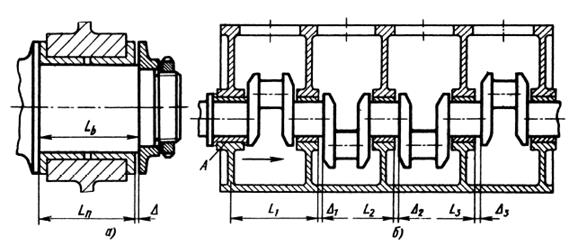Примером может служить конструкция фиксирующего подшипника скольжения (рис. 8.11, а). Пусть вал изготовлен из стали с коэффициентом линейного расширения а₁, а корпус подшипника — из сплава с коэффициентом а₂. Рабо­чие температуры соответственно равны t₁ и t₂.

Рис. 8.11. Термические торцовые зазоры.

Торцовый холодный зазор A = L_B — L_n, где L_B и L_n — соответственно
длины шейки вала и подшипника.

При нагреве до рабочей температуры t₁ длина шейки вала

L'_B = = L_B [1 + а₂ (t ₁ - t₀)], длина подшипника ,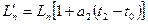

где t₀ — температура сборки.

Торцовый зазор в рабочем состоянии

∆^! = ∆ + .

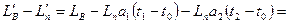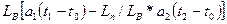Так как отношение 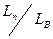весьма близко к единице, то можно принять

∆^! = ∆ + ∆_t, где ∆_t, — термическое изменение зазора:

∆_t= 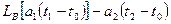(8.22)

В зависимости от соотношения величин а₁, а₂; и t₁ ,t₂ первоначальный зазор может увеличиться или уменьшиться. Опасен последний случай, так как вал может оказаться защемленным по торцам.

Пусть корпус подшипника изготовлен из алюминиевого сплава с

а₂ = 13 • 10^-6 1/°С, а вал из стали с а₂= 11 • 10^-6 1/°С; рабочая температура корпуса 100^сС, а вала 50°С, длина шейки вала 100 мм, температура сборки 20°С и первоначальный холодный зазор 0,05 мм. Термическое изменение зазора по уравнению (8.22) ∆_t =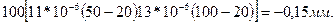

Горячий зазор ∆^! = ∆ + ∆_t =0,05 -0,15 = -0,1мм.

Таким образом, в соединении возникает натяг 0,1 мм; вал будет защемлен в подшипнике. Если в рабочем состоянии должен быть обеспечен минимальный зазор, допустим 0,05 мм, то первоначальный холодный зазор должен быть равен 0,05 + 0,15 = 0,2 мм.

Выбор правильных торцовых зазоров имеет особое значение для многоопорных валов с подшипниками, находящимися на большом расстоянии (один от другого (рис. 8.11, б).

Пусть передний подшипник А является фиксирующим. При нагреве картер удлиняется в направлении, указанном стрелкой. Во избежание защемления вала необходимо между щеками вала и торцами соответствующих подшипников предусмотреть зазоры ∆₁ ; ∆₂ ; ∆₃ , пропорциональные расстояниям L₁, L₂ и L₃ этих подшипников от базы. Сохраняя численные значения а₁ , а₂ , а₃, t₀, t₁ и t₂ предыдущего примера и полагая L₁ = 300, L₂ = 500 и L₃ = 700 мм, получаем следующие величины термического изменения зазоров:

∆₁ = 300 (-0,0015) = -0,45 мм; ∆₂ = 500(-0,0015) = -0,75 мм;

∆₃ = 700(-0,0015) = -1,05 мм.

При назначении конструктивных зазоров к этим величинам следует прибавить первоначальные холодные зазоры, которые устанавливают помощью размерного анализа по допускам на изготовление.

Расположение фиксирующих баз.

Фиксирующие базы следует выбирать с таким расчетом, чтобы при всех возможных температурных изменениях размеров системы точность расположения деталей не нарушалась или нарушалась бы в наименьшей мере.

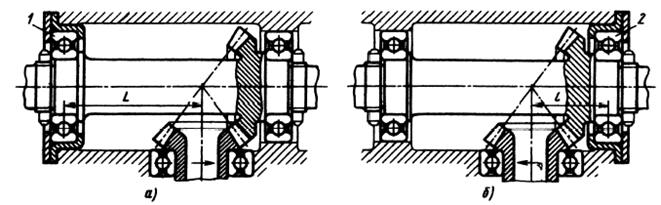
Рис. 8.12. Фиксация вала конической передачи

В узле конической передачи, установленной в корпусе из легкого сплава (рис. 8.12, а), фиксирующий подшипник 1 расположен на значительном расстоянии L от центра зацепления зубчатых колес. Удлинение корпуса при нагреве вызывает смещение малого колеса передачи в направлении, указанном стрелкой. Большое колесо перемещается в том же направлении, но на меньшую величину (вследствие меньшего значения коэффициента линейного расширения стального вала). В результате зазор в зацеплений уменьшается. При известных соотношениях зубчатые колеса могут начать работать враспор.

В правильной конструкции (рис. 8.12, б) фиксирующим является задний подшипник 2, расположенный на сравнительно малом расстоянии l от центра зацепления. Смещения колес относительно друг друга при нагреве здесь гораздо меньше; кроме того, зазор в зацеплении с нагревом уве­личивается, а не уменьшается, как в предыдущем случае.

Обеспечение свободы тепловых деформаций.

Следует избегать осевой фиксации деталей в двух точках. При наличии температурных 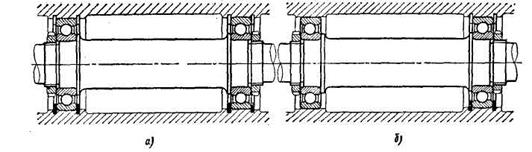деформаций в случае такой фиксации могут появиться термические напряжения, вызван­ные торможением смежности.

Рис. 8.13. Фиксация подшипников качения

Примером ошибочной установки яв 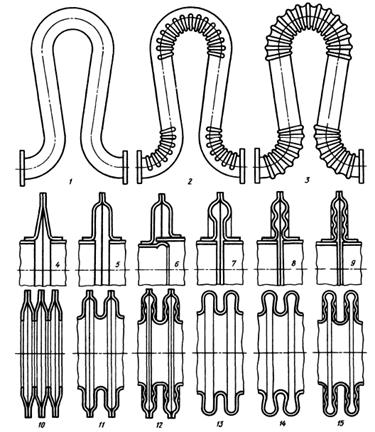ляется фиксация вала в двух под­шипниках качения одновременно (рис. 8.13, а). Если корпус подшипников выполнен из материала с иным коэффициентом линейного расширения, чем вал, а также если вал и корпус имеют различные рабочие темпера­туры, то в узле возникает зазор или натяг, вызывающий защемление подшипников. Неизбежные погрешности выполнения осевых размеров со­единения, в свою очередь, могут вызвать появление зазоров или натягов.

Вал следует фиксировать в одном подшипнике (рис.8.13,6).

Рис. 8.14. Компенсаторы термического расширения

Второй подшипник должен быть плавающим, т. е. иметь свободу перемещения в осевом направлении.

В соединениях трубопроводов, несущих горячие жидкости или газы, необходимо предусматривать компенсаторы тепловых расширений, пред­отвращающие возникновение термических усилий и деформацию трубо­проводов.

Компенсаторы типа «лира» (рис. 8.14, 1-3) имеют большие размеры. Более компактны линзовые (4-9) и особенно сильфонные компенсаторы (10-15).

Из приведенного рисунка понятно, что в соединениях, работающих при повышенных температурах, сопрягаемые детали меняют своё первоначальное положение. В ряде случаев необходим тепловой расчёт для определения их положения в пространстве при нагреве или даже корректировка формы сопрягаемых деталей.

На рис. 8.15 показано необходимое придание конусности штоков выхлопных клапанов двигателей внутреннего 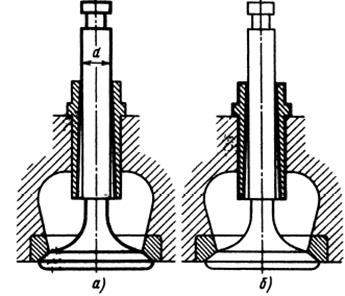сгорания. Так как рабочая температура верхнего конца штока ниже температуры в шейке (на участке перехода штока в головку), то диаметр верхнего конца штока должен быть (из условия постоянства зазора по длине направляющей) больше диаметра штока у шейки на величину 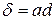∆_t, где d – номинальный размер штока; а - коэффициент линейного расширения материала клапана;

∆_t - разность температур шейки и верхнего конца штока.

Рис. 8.15. Корректировка формы клапана и направляющей.

Для клапана из аустенитной стали (а= 20*10^-6 1/ ⁰С) при диаметре штока

d = 12мм и ∆_t = 200⁰ С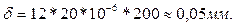

Корректировку можно также осуществить, выполнив отверстие клапана конически расширяющимся по направлению к головке клапана (рис. 8.15, б). И тот и другой способ облегчают самоустановку клапана в седле.