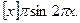Полученной при вращении циклоиды
Найти вычет функции в указанной особой точке: z-a.
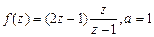
Решение:
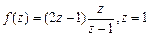
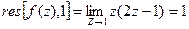
Ответ: 1.
Найти вычет функции в указанной особой точке: z-a.
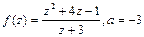
Решение:
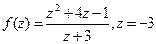
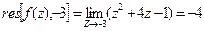
Ответ: -4.
№7. Вычислить интеграл по замкнутому контору, считая направление обхода положительным:
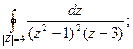
Решение:
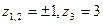
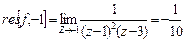
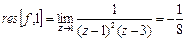
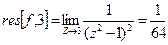
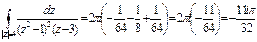
Ответ: т.к. считаем направление обхода положительным, то 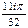
№8. Вычислить интеграл по замкнутому контору, считая направление обхода положительным:
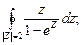
Решение: z=0; 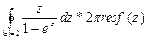 ;
;
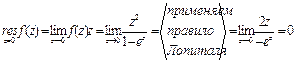
Ответ:0.
№9. Вычислить интеграл по замкнутому контору, считая направление обхода положительным:
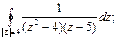
Решение:
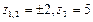
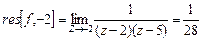
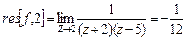
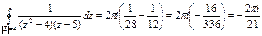
Ответ: т.к. считаем направление обхода положительным, то 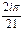
№10. Вычислить интеграл 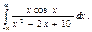
Решение:
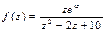 ,
, 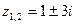 - особые точки.
- особые точки.
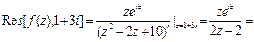
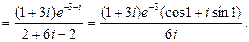
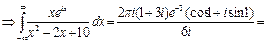
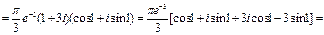
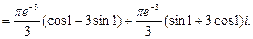
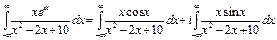
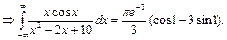
Ответ: 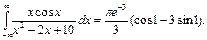
№11. Вычислить интеграл: 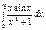
Решение: 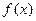 - чётная
- чётная 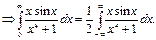
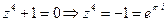 .
.
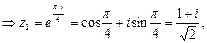
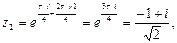
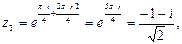
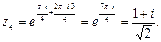
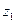 и
и 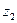 лежат в верхней полуплоскости.
лежат в верхней полуплоскости. 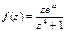
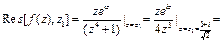
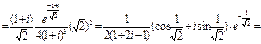
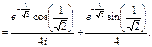
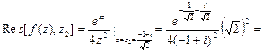
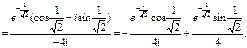
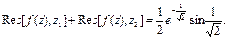
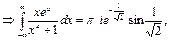
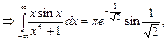
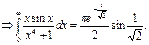 Ответ:
Ответ: 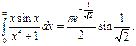
№12. Указать направление наибольшего убывания функции 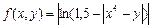 в точке с координатами
в точке с координатами 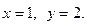
Решение:
1 способ:В окрестности точки 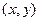 функция
функция 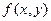 имеет вид:
имеет вид:
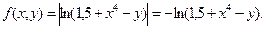
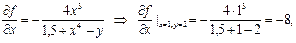
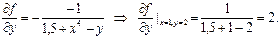
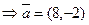 .
.
2 способ:
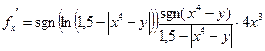
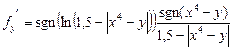
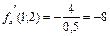
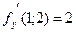
-grad=8i-2j
Ответ: 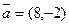 .
.
№13. Написать уравнение прямой, проходящей через точку с координатами 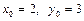 , которая ортогональна в этой точке к линии уровня функции
, которая ортогональна в этой точке к линии уровня функции 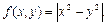
Решение:
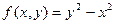 в точке
в точке 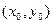 .
.
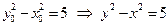 - линия уровня проходящая через
- линия уровня проходящая через 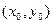 .
.
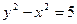 Продифференцируем по x:
Продифференцируем по x:
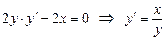
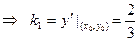 - угловой коэффициент касательной к линии уровня в точке
- угловой коэффициент касательной к линии уровня в точке 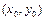 .
.
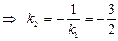 - угловой коэффициент нормали.
- угловой коэффициент нормали.
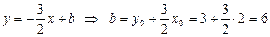
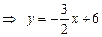 .
.
Ответ: 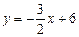 .
.
№14. Написать уравнение прямой, проходящей через точку с координатами 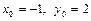 , которая касается в этой точке линии уровня функции
, которая касается в этой точке линии уровня функции 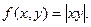
Решение:
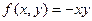 - уравнение функции в точке
- уравнение функции в точке 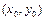 .
.
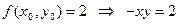 - уравнение линии уровня.
- уравнение линии уровня.
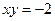 Продифференцируем:
Продифференцируем:
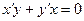
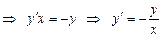
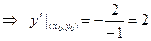 - угловой коэффициент касательной.
- угловой коэффициент касательной.
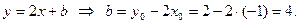
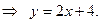
Ответ: 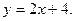
№15. Указать направление наибольшего роста функции 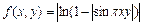 в точке с координатами
в точке с координатами 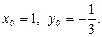
Решение:
В точке 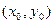 функция
функция 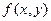 имеет вид:
имеет вид:
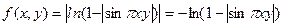
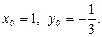
В точке 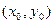 функция
функция 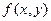 имеет вид:
имеет вид:
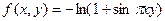
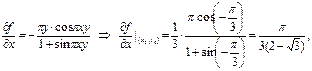
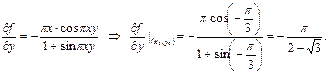
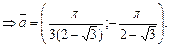 Ответ:
Ответ: 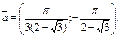
№16. Доказать, что кривые 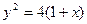 и
и 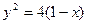
Пересекаются под прямым углом.
Решение:
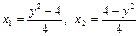
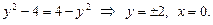
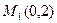 и
и 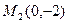 - точки пересечения кривых.
- точки пересечения кривых.
В точке 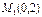 :
:
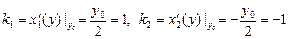
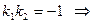 касательные перпендикулярны в точке
касательные перпендикулярны в точке 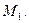
В точке 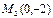 :
:
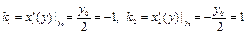
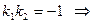 касательные перпендикулярны в точке
касательные перпендикулярны в точке 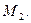
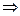 в обеих точках пересечения кривые перпендикулярны.
в обеих точках пересечения кривые перпендикулярны.
Написать уравнение касательной
в циклоиде: x=2(t-sint), y=2(1-cost) в точке
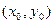 соответствующей
соответствующей 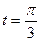 .
.
Решение:
Уравнение касательной имеет вид:
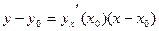
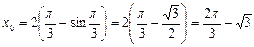
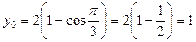
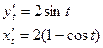
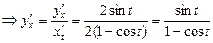
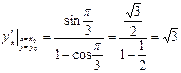
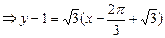
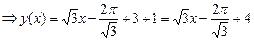
Ответ: 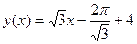
№18. В каких точках пространства градиент функции перпендикулярен оси Oz: 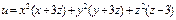
Решение:
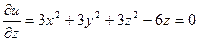
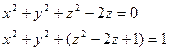
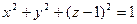 - сфера радиуса R=1 с центром в точке (0;0;1)
- сфера радиуса R=1 с центром в точке (0;0;1)
Ответ: (0;0;1)
№19. Вычислить объем тела, ограниченного поверхностью,
полученной при вращении циклоиды
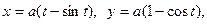 около оси Ox,
около оси Ox,
при 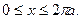
Решение:
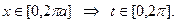
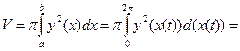
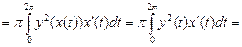
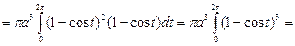
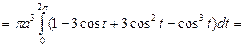
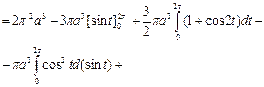
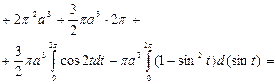
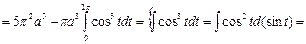
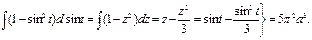
Ответ: 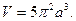
№21. Вычислить:
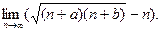
Решение:
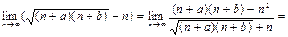
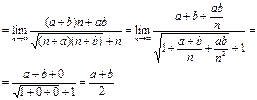 .
.
Ответ: 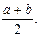
№22. Вычислить: 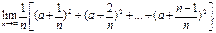
Решение:
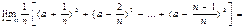
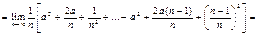
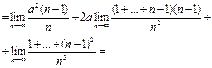
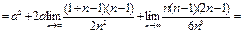
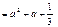 Ответ:
Ответ: 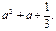
№23. Последовательность 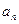
задается формулами: 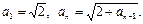
Вычислить 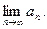
Решение:
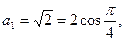
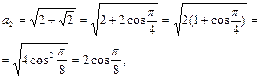

…
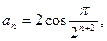
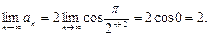
Ответ: 2.
№25. Вычислить 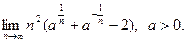
Решение:
1 способ:
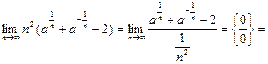
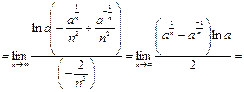
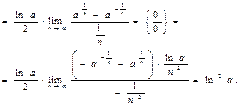
2 способ:
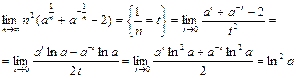
Ответ: 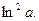
№26. Вычислить: 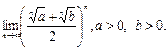
Решение:
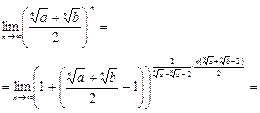
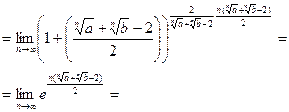
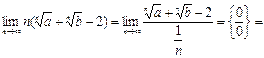
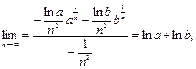
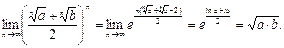
Ответ: 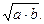
№27. Вычислить: 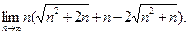
Решение:
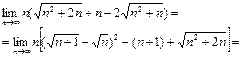
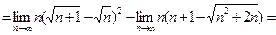
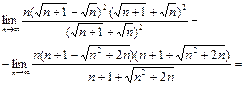
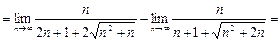
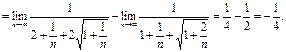
Ответ: 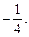
№28. Найти предел: 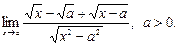
Решение:
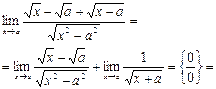
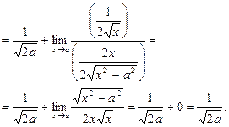
Ответ: 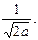
№29. Найти предел: 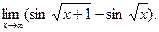
Решение:
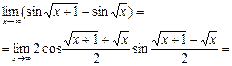
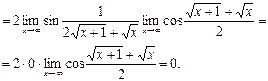
Ответ: 0.
№30. Найти предел: 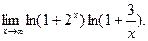
Решение:
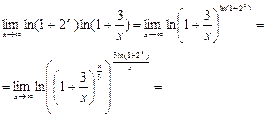
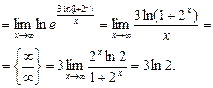
Ответ: 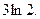
№31. Показать, что функция 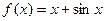 равномерно непрерывна на всей оси
равномерно непрерывна на всей оси 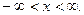
Решение:Ф-я f(x) наз-ся
равномерным непрерывным на x,
если для любого 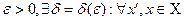
удовлетворяющий 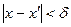
выполняется 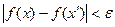
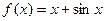 ,
,
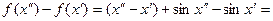
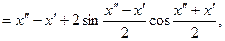
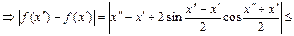
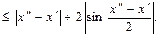
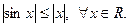
№32. Найти производную функции 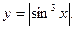
Решение:
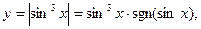
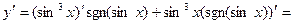
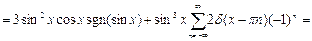
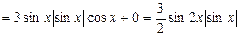 .
.
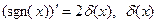 - дельта-функция Дирака.
- дельта-функция Дирака.
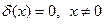 и
и 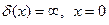 .
.
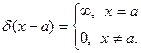
Ответ: 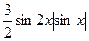 .
.
№33. Найти производную функции 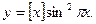
Решение: 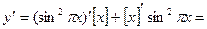
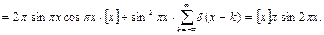
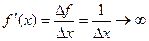 при
при 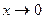
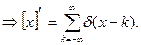
Ответ: