Заметим, что не всякая линия является графиком функции

Определение 6: Функция называется явной, если она задана формулой y=f(x).

Определение 7: Функция называется неявной, если она задана уравнением F(x; у)=0.

Способы задания функции.

Существуют три основных способа задания функций: аналитический, табличный и графический.

1) Аналитический способ - зависимость между переменными величинами определяется с помощью формулы, указывающей, какие и в каком порядке действия нужно выполнить, чтобы получить значение функции, соответствующее данному значению аргумента.

2) Табличный способ - зависимость между переменными величинами определяется с помощью указанной таблицы. Область определения – множество чисел, расположенных в первой строке (столбце) таблицы, область значений – множество чисел, расположенных во второй строке (столбце) таблицы. Так задаются функции с конечными значениями.

3) Графический способ - зависимость между переменными задаётся посредством графика.

Определение 1: Если на некотором множестве X определена функция z=j(x) со множеством значений Z, а на множестве Z - функция y=f(z), то функция у=f[j(х)] называется сложной функцией от х (или суперпозицией функций j(x)и f(z)), а переменная z - промежуточной переменной сложной функции.

Определение 2: Пусть X и Y—некоторые мно­жества и пусть задана функция f, т. е. множество пар чисел (х; у) (хÎX, уÎY), в котором каждое число х входит в одну и только одну пару, а каждое число y - по крайней мере в одну пару. Если в каждой паре этого множества числа х и у поменять местами, то получим множество пар чисел (у; х), которое называется обратной функцией j к функции f.

Обратная функция в данном понимании может функцией и не являться.

Функция может быть задана параметрически на множестве Х посредством переменной t, называемой параметром:

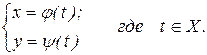
Классификация функций.

Определение 1: Простейшими элементарными функциями являются:

· постоянная функция f(х)=С, С=const,

· степенная функция f(х)=х^a (a—любое число),

· показательная функция f(х)=а^х (0<а¹1),

· лога­рифмическая функция f(х)=log_aх (0<а¹1),

· тригонометри­ческие функции f(х)=sinx, f(х)=cosx, f(х)=tgx, f(х)=ctgx,

· обратные тригонометрические функции f(х)=arcsinx, f(х)=arccosx, f(х)=arctgх, f(х)=arcctgx.

Определение 2: Все функции, получаемые с помощью конечного числа арифметических действий над простейшими элементарными функциями, а также суперпозицией этих функций, составляют класс элементарных функций.

На основании определения следует, что элементарные функции являются функции заданные аналитически.

Классификация элемен­тарных функций:

1) Функция вида Р(х)=a₀х^m+a₁х^m-1+…+a_m-1х+a_m, где m³0 - целое число, a₀, a₁, …, a_m-1, a_m любые числа — коэффициенты (а₀¹0), называется целой ра­циональной функцией или многочленом степени m. Многочлен первой степени называется также линейной функцией.

2) Функция, представляющая собой отношение двух целых рациональных функций

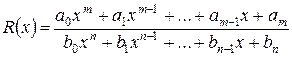, называется дробно-рациональной функцией.

Совокупность целых рациональных (1) и дробно-рацио­нальных (2) функций образует класс рациональных функций.

3) Функция, полученная с помощью конечного числа суперпозиций и четырех арифметических действий над степенными функциями как с целыми, так и с дробными показателями и не являющаяся рациональ­ной, называется иррациональной.

Алгебраические функции: рациональ­ные (1 и 2) и иррациональные (3).

4) Всякая функция, не являющаяся алгебраической, называется трансцендентной функцией.

Лекция 6

Числовая последовательность

Бесконечно малые и бесконечно большие последовательности

Предел числовой последовательности