Ортогональные линейные преобразования

Определение 53. Линейное преобразование j евклидова пространства Е называется ортогональным, если для любых векторов а и в из Е выполняется условие (а, в) = (j(а), j(в)). (49)

Свойства ортогональных преобразований.

Пусть j – ортогональное преобразование пространства Е.

1⁰. | а| = |j(а)| для любого вектора а.

| а| = 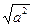= = 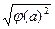| j(а)|.

2⁰. 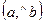= 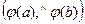для любых векторов а и .

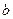3⁰. Пусть Е_n конечномерное евклидово пространство, е = (е₁, е₂,... , е_n) – базис в нём, А – матрица преобразования j и Г – матрица Грама в этом базисе. Тогда j(а) = А×х, j( 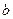) = А×у, где х и у –столбцы координат векторов а и 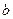соответственно; (а, 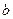) = х^Т×Г×у, (j(а), j( 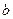)) = (А×х)^Т×Г×( А×у) = х^Т×(А^Т×Г×А)×у. Так как (а, 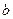) = (j(а), j( 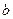)), то Г = А^Т×Г×А. Итак, матрица ортогонального преобразования удовлетворяет условию

Г = А^Т×Г×А (50)

Справедливо и обратное. Если в Е_n зафиксирован базис и Г – матрица Грама в этом базисе, то матрица А, удовлетворяющая условию (48), задаёт ортогональное преобразование.

Если базис е = (е₁, е₂,... , е_n) ортонормированный, то Г = Е и формула (50) примет вид

А^Т× А = Е, или А^Т = А^–1.

Определение 54. Квадратная матрица А называется ортогональной, если

А^Т = А^–1 (51).

Теорема 48.Линейное преобразование евклидова пространства является ортогональным тогда и только тогда, когда в ортонормированном базисе оно задаётся ортогональной матрицей.

Доказательство следует из свойства 3⁰ и определения 53.

Теорема 49.Квадратная матрица является ортогональной тогда и только тогда, когда сумма квадратов всех элементов любого столбца (или строки) равна 1, а сумма попарных произведений соответствующих элементов двух различных столбцов (или строк) равна нулю.

Доказательство следует из формулы 51.

Теорема 50.Линейное преобразование евклидова пространства является ортогональным тогда и только тогда, когда оно ортонормированный базис переводит в ортонормированный базис.

Доказательство. Þ Пусть j : Е_n ® Е_n ортогональное преобразование и пусть е = (е₁, е₂,... , е_n) ортонормированный базис в Е_n . Если А – матрица этого преобразования в базисе е, то А – ортогональная. Но тогда j(е) = е×А. Распишем это равенство, если

А = .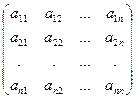

Получим j(ек) = а1ке1 + а2ке2 + … + аnкеn . Так как базис е ортонормированный, то (j(ек))2 = 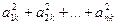= (ек)2 = 1, т.е. все векторы j(ек) единичной длины. По той же причине (j(ек), j(ер)) = а1к×а1р + а2к×а2р + … + аnк×аnр = (ек , ер ) = 0,

если к ¹ р, т.е. j(е_к) ^ j(е_р). Так как векторы системы j(е) попарно ортогональны, то они линейно независимы, т.е. j(е) – базис. Итак, j(е) – ортонормированный базис.

Ü Пусть е и j(е) – ортонормированные базисы. Тогда 1 = (j(е_к))² = 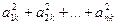и 0 = (j(е_к), j(е_р)) = а_1к×а_1р + а_2к×а_2р + … + а_nк×а_nр при к ¹ р. Следовательно, по теореме 49, матрица А – ортогональная.

Теорема 51. Если матрица А ортогональная, то |А | = ± 1.

Действительно, если матрица А ортогональная, то А^Т× А = Е. Отсюда |А^Т×А | = |Е |, |А^Т|×| А| = 1, |А|×|А| = 1, |А|² = 1, |А| = ±1.

Теорема 52. Собственные значения ортогонального преобразования могут быть только 1 или (–1).

Доказательство. Пусть l – собственное значение ортогонального преобразования j.

Тогда существует такой ненулевой вектор (х₁, х₂, … , х_n )^Т, что А×х = l×х, где А – матрица преобразования j. Равенство транспонируем и перейдём к сопряжённым числам, получим 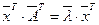. Перемножим почленно оба равенства. 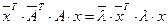. Так как А – действительная ортогональная матрица, то 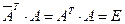. Следовательно, 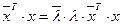. Отсюда 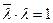, т.е. |l|² = 1. Но это и значит, что собственными значениями могут быть только числа 1 и (–1).

Теорема53. Собственные векторы ортогонального преобразования, принадлежащие различным собственным значениям ортогональны.

Доказательство. Для любых а и в из Е_n имеет место (а, в) = (j(а), j(в)) = (l₁а, l₂в) = = l₁l₂(а, в). Так как l₁ ¹ l₂, то, согласно предыдущей теоремы, l₁ =1, l₂ = –1. Следовательно, (а, в) = – (а, в). Отсюда (а, в) = 0. Так как а и в не нулевые, то они ортогональные.