Выбераем разрешающий элемент
СОДЕРЖАНИЕ
1.Задача линейного программирования. Симплекс метод
2. Транспортная задача
3. Динамическое программирование
4. Сетевое планирование и управление
Задача линейного программирования. Симплекс метод.
Автопредприятие имеет n автомобилей и отправляет их на m маршрутов. Для погрузки и выгрузки предприятие и клиенты располагают погрузочно-разгрузочной техникой: автокранами – 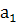 , автопогрузчиками –
, автопогрузчиками – 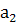 , стационарными кранами –
, стационарными кранами – 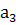 , кранами на гусеничном ходу –
, кранами на гусеничном ходу – 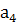 . Затраты времени на оборот автомобиля на маршрутах соответственно
. Затраты времени на оборот автомобиля на маршрутах соответственно 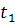 ,
, 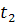 ,
, 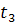 ,
, 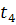 , затраты времени на выполнение погрузочно-разгрузочных работ техникой: в – автокранами, p – автопогрузчиками, ф – стационарными кранами, г – кранами на гусеничном ходу.
, затраты времени на выполнение погрузочно-разгрузочных работ техникой: в – автокранами, p – автопогрузчиками, ф – стационарными кранами, г – кранами на гусеничном ходу.
Решить задачу как оптимизационную по максимальному использованию имеющейся техники.
| Виды техники | Маршруты, m | ∑ | |||
| Автомобили | 220/ 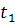 | 170/ 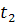 | 50/ 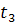 | 190/ 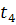 | |
| Автокраны | 75/ 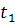 | 105/ 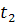 | 30/ 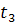 | 60/ 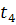 | |
| Автопогрузчики | 65/ 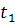 | 60/ 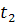 | 75/ 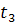 | 45/ 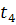 | |
| Стационарные Краны | 65/ 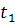 | - | - | - | |
| Краны на гусеничном ходу | - | - | 100/ 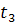 | - |
Выразив автокраны, автопогрузчики, стационарные краны и краны на гусеничном ходу через автомобили получаем следующие неизвестные:
X1, X2, X3, X4 – количество автомобилей на первом, втором, третьем и четвертом маршрутах соответственно.
Составляем систему ограничений
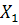 +
+ 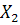 +
+ 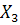 +
+ 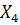 ≤ 170
≤ 170
0.34 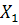 + 0.61
+ 0.61 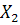 + 0.6
+ 0.6 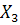 + 0.31
+ 0.31 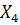 ≤ 9
≤ 9
0.29 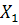 + 0.35
+ 0.35 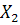 + 1.5
+ 1.5 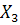 + 0.23
+ 0.23 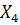 ≤ 13
≤ 13
0.29 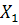 ≤ 14
≤ 14
2 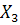 ≤ 6
≤ 6
Составляем функцию цели
X1+X2+X3+ X4 + 0.34X1 + 0.61X2 +0.6X3 + 0.31X4 + 0.29X1 + 0.35X2 + 1.5X3 + 0.23X4 +0.29X1 +2X3
MAX
1.92 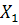 + 1.45
+ 1.45 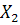 + 5.1
+ 5.1 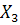 + 1.54
+ 1.54 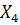 MAX
MAX
Из неравенств составляем равенства
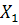 +
+ 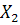 +
+ 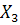 +
+ 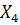 +
+ 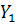 = 170
= 170
0.34 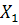 + 0.61
+ 0.61 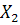 + 0.6
+ 0.6 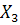 + 0.31
+ 0.31 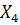 +
+ 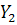 = 9
= 9
0.29 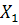 + 0.35
+ 0.35 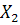 + 1.5
+ 1.5 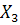 + 0.23
+ 0.23 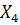 +
+ 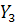 = 14
= 14
0.29 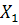 +
+ 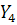 = 4
= 4
2 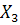 +
+ 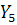 = 6
= 6
Где 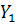 ,
, 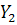 ,
, 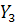 ,
, 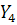 ,
, 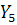 – количество неиспользованной техники соответственно
– количество неиспользованной техники соответственно
Выразим неиспользованную технику из уравнений
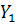 = 170 – (
= 170 – ( 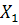 +
+ 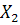 +
+ 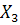 +
+ 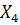 )
)
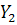 = 9 – (0.13
= 9 – (0.13 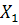 + 0.11
+ 0.11 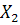 + 0.3
+ 0.3 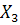 + 0.25
+ 0.25 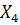 )
)
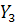 = 14 – (0.2
= 14 – (0.2 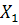 + 0.13
+ 0.13 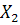 + 0.95
+ 0.95 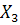 + 0.21
+ 0.21 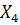 )
)
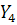 = 4– 0.2
= 4– 0.2 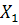
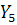 = 6 – 1.15
= 6 – 1.15 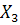
Функцию цели приравниваем к 0
F = 1.92 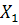 + 1.45
+ 1.45 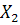 + 5.1
+ 5.1 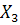 + 1.54
+ 1.54 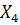 MAX
MAX
F = - 1.92 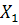 - 1.45
- 1.45 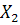 - 5.1
- 5.1 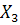 - 1.54
- 1.54 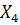 = 0
= 0
Составляем первую симплекс таблицу
В первую симплекс таблицу заносятся коэффициенты при свободных неизвестных из системы уравнений. Все известные в системе уравнений делятся на свободные и базисные.
- 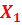 | - 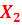 | - 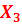 | - 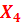 | ||
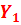 | |||||
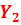 | 0.34 | 0.61 | 0.6 | 0.31 | |
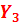 | 0.29 | 0.35 | 1.5 | 0.23 | |
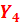 | 0.23 | ||||
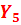 | |||||
| C | -1.92 | -1.95 | -5.1 | -1.54 |
Для того, чтобы перейти к новому базисному плану необходимо свободные и базисные поменять местами так, чтобы в конечном результате C ≥ 0.
Произведем улучшение начального базисного плана, для этого необходимо найти такие базисную и свободную, которые необходимо поменять местами, а в результате будет получена новая матрица с новым планом. Для этого существует алгоритм симплекс метода:
Выбераем разрешающий элемент
1.1 Выбираем разрешающий столбец. Находим в строке С наибольший по модулю отрицательный элемент (-3,4) и покажем им разрешающий столбец.
1.2 Выбираем разрешающую строку. Для этого рассмотрим все положительные элементы разрешающего столбца. 0 и отрицательные элементы не рассматриваются. Делим свободные члены на элемент разрешающего столбца а данной стороке. Минимальное из отношений показывает на разрешающую строку.
На пересечении разрешающего столбца и разрешающей строки находится разрешающий элемент.
Разрешающий элемент показывает, какую свободную и базисную необходимо поменять местами.
2. В новой матрице элемент, стоящий на месте разрешающего элемента предыдущей матрицы получается путем деления единицы на разрешающий элемент: 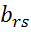 =
= 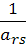 ,
, 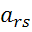 - разрешающий элемент.
- разрешающий элемент.
Остальные элементы, стоящие на месте разрешающей строки определяются делением соответствующих элементов предыдущей матрицы на разрешающий элемент: 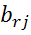 =
= 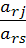 ,
, 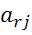 - элемент разрешающей строки.
- элемент разрешающей строки.
Остальные элементы, стоящие на месте разрешающего столбца определяются аналогично, но знак меняется на противоположный:
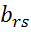 =
= 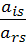 ,
, 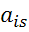 - элемент разрешающего столбца.
- элемент разрешающего столбца.
Все другие элементы новой матрицы определяются по формуле:
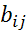 =
= 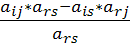
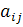 – соответствующий элемент предыдущей матрицы
– соответствующий элемент предыдущей матрицы
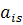 - элемент предыдущей матрицы, стоящий на пересечении строки i рассматриваемого элемента и разрешающего столбца.
- элемент предыдущей матрицы, стоящий на пересечении строки i рассматриваемого элемента и разрешающего столбца.
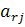 - элемент предыдущей матрицы, стоящий на пересечении разрешающей строки и столбца j рассматриваемого элемента.
- элемент предыдущей матрицы, стоящий на пересечении разрешающей строки и столбца j рассматриваемого элемента.
Улучшения производятся до тех пор, пока в С строке не будет отрицательных элементов.
Вторая симплекс таблица
| -X1 | -X2 | -X3 | -X4 | ||
| Y1 | -0.5 | ||||
| Y2 | 0.4 | 0.61 | -0.3 | 0.31 | 7.2 |
| Y3 | 0.29 | 0.35 | -0.75 | 0.23 | |
| Y3 | 0.23 | ||||
| X3 | 0.5 | 0.3 | |||
| C | -1.92 | -1.95 | 2.55 | -1.54 | 30.6 |
Переходим к следующему улучшению, т.к. в строке С есть отрицательные элементы.
