Работа внутренних сил плоской стержневой системы

Рассмотрим два состояния плоской стержневой системы, представленной рамой.

Обозначим через M₁, Q₁, N₁ внутренние силы первого, а через M₂, Q₂, N₂ – внутренние силы второго состояния. Последним будут соответствовать деформации κ₂, g₂, e₂ и перемещения u₂, v₂, q₂ , связанные зависимостями из §1.3:

dN₂/dx = – q_x; ü

dQ₂/dx = q_y; ý (1.10¢)

dM₂/dx = Q₂ . þ

κ ₂ = dq₂/dx; ü

g₂ = q₂ – dv₂/dx; ý (1.11¢)

e₂ = du₂/dx . þ

κ ₂ = M₂/EJ; ü

g₂ = mQ₂/GF; ý (1.12¢)

e₂ = N₂/EF. þ

Напомним, что по отношению к элементу рамы длиной dx внутренние силы, несмотря на название, являются такими же внешними, как и равнодействующая распределенной нагрузки (рис. 3.10, а).

Вычислим работу внутренних сил M₁, Q₁, N₁ на перемещениях второго состояния системы (рис. 3.10, б):

dA₁₂ = - N₁u₂ + (N₁ + dN₁)(u₂ + du₂) + Q₁v₂ – (Q₁ + dQ₁)(v₂ + dv₂) - M₁q₂ +

+ (M₁+ dM₁)( q₂+dq₂) +q_xdx(u₂ + du₂/2) + q_ydx(v₂ + dv₂/2) = - N₁u₂ + N₁u₂ + N₁du₂ + +{dN₁u₂}+ dN₁du₂ + Q₁v₂ - Q₁v₂ - Q₁dv₂ -{dQ₁v₂} - dQ₁dv₂ - M₁q₂ +M₁q₂ + M₁dq₂ + + {dM₁q₂} + dM₁ dq₂ + q_xdx(u₂+du₂/2) + q_ydx(v₂+dv₂/2). (3.12)

θ2

v2+dv2

dx

u2

M1 + dM1

N1 + dN1

Q1 + dQ1

dx

M11

N11

Q11

а)

б)

qy·dx

qx·dx

v2

u2+du2

θ2+dθ2

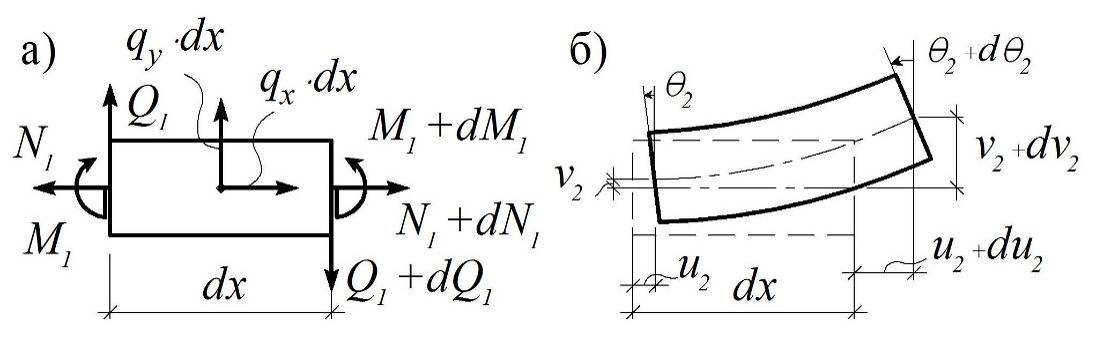
Рис. 3.10

Пренебрегая в (3.12) подчеркнутыми слагаемыми как бесконечно малыми второго порядка и воспользовавшись соотношением (1.10) для членов в фигурных скобках, получим:

dA₁₂ = N₁du₂ – {Q₁dv₂} + M₁dq₂ – {q_x dxu₂}+ q_x dxu₂ + q_xdxdu₂/2 – {q_y dxv₂} +

+ q_y dxv₂ + q_ydxdu₂/2 + Q₁dxq₂. (3.13)

Снова, отбрасывая в последнем выражении подчеркнутые слагаемые как бесконечно малые второго порядка и используя (1.11¢) для второго члена, заключенного в фигурные скобки, будем иметь:

dA₁₂ = N₁e₂dx + M₁κ ₂dx – Q₁(q₂ –g₂)dx + Q₁dxq₂ =

= (M₁κ ₂ + Q₁g₂ + N₁e₂)dx. (3.14)

Наконец, выражая в (3.14) деформации через внутренние усилия с помощью (1.12¢), найдем для элемента рамы длиной ds:

dA₁₂ = ( M₁M₂/EJ + mQ₁Q₂/GF + N₁N₂/EF ) ds.

Полная работа получается интегрированием по длине стержня и суммированием по всем участкам рамы. С учетом знака получим окончательное выражение работы внутренних сил первого состояния на перемещениях второго состояния:

W₁₂ = - A₁₂ = - Sò ( M₁M₂/EJ + mQ₁Q₂/GF + N₁N₂/EF ) ds. (3.15)

Интеграл Мора-Максвелла

С помощью (3.15) нетрудно получить формулу для определения перемещения i-й точки упругой системы от приложенной нагрузки.

Рассмотрим два состояния системы: первое – от заданной нагрузки и второе – от единичной силы или единичного момента, приложенных в точке i в направлении искомого линейного или, соответственно, углового перемещения (рис. 3.11). Обычно первое из этих состояний называют действительным, а второе – возможным или виртуальным.

i'

Pi =1

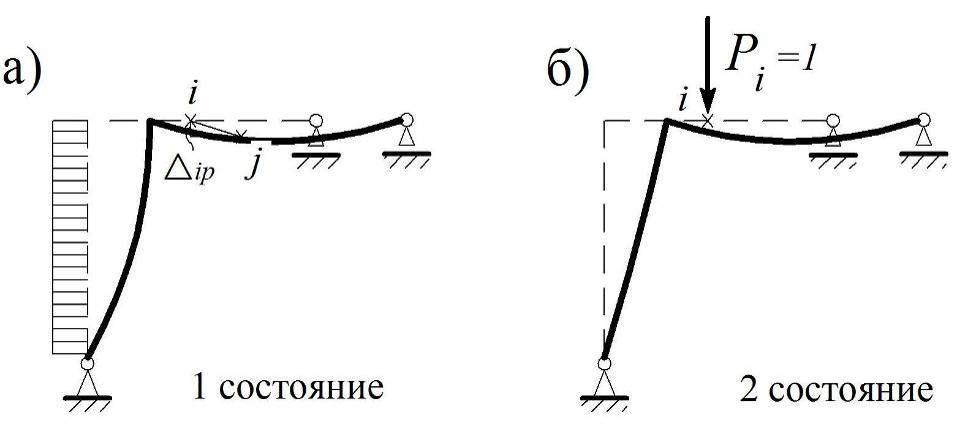
Рис. 3.11

Обозначим через D_ip искомое перемещение точки i – в нашем примере на рис. 3.11, а – это вертикальное линейное перемещение.

Пусть M_p, Q_p, N_p – внутренние усилия первого состояния, а`M<sub>i</sub>, `Q_i, `N_i – внутренние силы второго состояния.

Воспользовавшись теоремой Бетти:

A₁₂ = A₂₁,

где

A₂₁ = P_i×D_ip = 1×D_ip = D_ip,

а

A₁₂ = – W₁₂,

получим с помощью (3.15) искомую формулу для определения перемещений, которая называется интегралом Мора-Максвелла:

D_ip = Sò ( M_p`M<sub>i</sub> /EJ + mQ<sub>p</sub>`Q_i /GF + N_p`N_i /EF )ds. (3.16)

Таким образом, для определения линейного (углового) перемещения точки i упругой системы в заданном направлении от заданной нагрузки необходимо:

– построить эпюры M_p, Q_p, N_p в заданной системе от заданной нагрузки;

– построить эпюры `M<sub>i</sub>, `Q_i, `N_i от единичной силы (единичного момента), приложенной в точке i в направлении искомого перемещения;

– вычислить интеграл (3.16).

Отметим, что перемещения в балках и рамах определяются в основном изгибными деформациями, поэтому для таких систем вместо (3.16) можно воспользоваться формулой:

D_ip = Sò ( M_p`M_i /EJ)ds . (3.17)

Наоборот, в фермах отсутствуют изгибающие моменты и поперечные силы, поэтому перемещения здесь полностью определяются продольными деформациями:

D_ip = ò (N_p`N<sub>i</sub> /EF ) ds=S(N<sub>pk</sub> `N_ik /EF_k)l_k, (3.18)

где l_k и EF_k – соответственно длина и продольная жесткость k-го стержня фермы.

Примечания

1. Вычисление интеграла (3.17) условно называют перемножением эпюр M_p и`M<sub>i</sub> и записывают это в виде: D<sub>ip</sub> = (M<sub>p</sub> ´`M_i).

2. При вычислении перемещений, как правило, пренебрегают деформациями сдвига.

3. При выводе формулы (3.16) нигде не предполагалось, что заданная система является статически определимой, поэтому эта формула верна как для СОС, так и для СНС. Тем не менее, в названии главы фигурируют только СОС поскольку, во-первых, пока в нашем распоряжении нет удобного метода определения внутренних усилий в СНС, а во-вторых, для последних систем формулу (3.16) можно упростить.

Формула Верещагина

Интеграл (3.17) можно вычислить аналитически, однако если жесткости стержней постоянны, удобнее воспользоваться другим способом, который обычно и применяют на практике.

Учитывая, что эпюра`M<sub>i</sub> от единичного силового фактора является кусочно-линейной, можно выбрать промежутки [a,b], где она будет просто линейной. Тогда выбирая начало локальной системы отсчета так, как показано на рис. 3.12, б, ее уравнение можно записать в виде: `M_i(x) = tga×x. При этом интеграл в (3.17) примет вид:

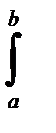( M_p`M_i /EJ)dx = (tga/EJ) 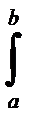x× M_p dx. (3.19)

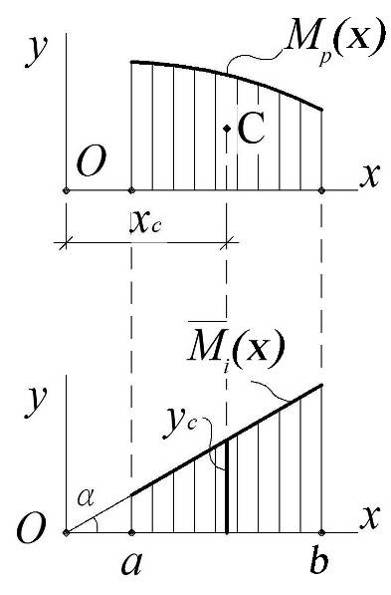
Рис. 3.12

Обозначая через w площадь эпюры M_p:

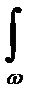w = dw = 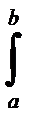M_p dx ,

и учитывая, что ее статический момент относительно оси Oy равен:

S_y = 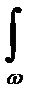xdw = w×x_c,

представим (3.19) в виде:

(tga/EJ) 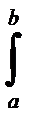x× M_p dx = (tga/EJ) 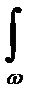xdw= (tga/EJ) x_c×w = (wy_c)/EJ,

где y_c = tga×x_c.

Возвращаясь к формуле (3.17), получим:

D_ip = S (w_ky_ck)/(EJ_k). (3.20)

Таким образом, чтобы перемножить две эпюры, из которых хотя бы одна является линейной, нужно вычислить площадь криволинейной эпюры – w и умножить ее на ординату y_c в линейной эпюре, вычисленную под центром тяжести криволинейной.

Для реализации формулы (3.20) остается рассмотреть геометрические характеристики стандартных эпюр (рис. 3.13), где две последние – соответствуют эпюрам от равномерно распределенной нагрузки. Поскольку любую нестандартную эпюру можно представить комбинацией стандартных, с помощью последних можно перемножить произвольные эпюры.

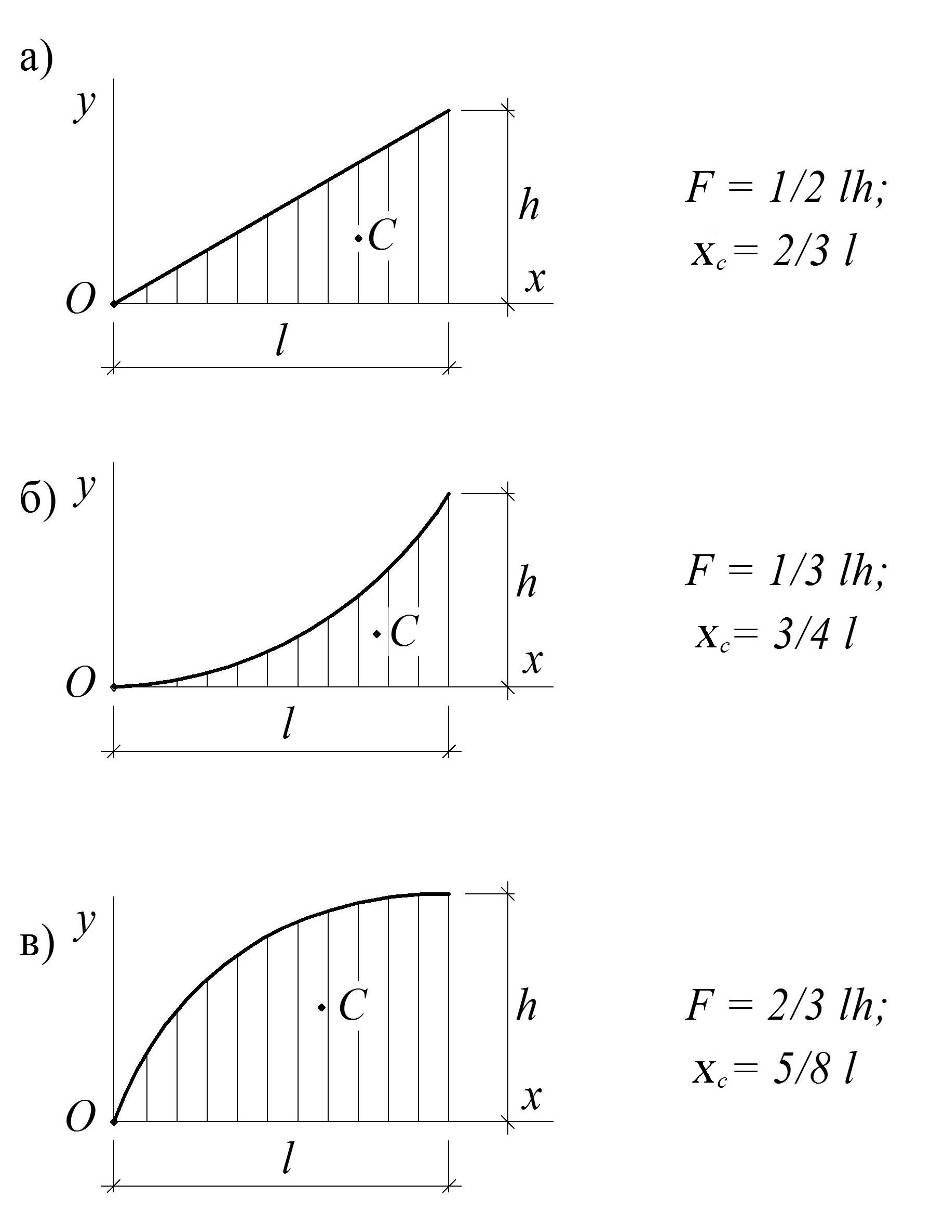
Рис. 3.13

Примечания

1. При выводе формулы (3.20) криволинейная эпюра M_p с площадью w предполагается однозначной. Если это условие не выполнено, ее представляют комбинацией двух или большего числа стандартных эпюр.

2. Для вычисления интеграла (3.17) можно применять формулы численного интегрирования, в том числе – формулу Симпсона:

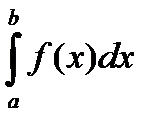= [ (b – a)/6] {f(a) + 4f [ (a + b)/2] + f(b)},

которая позволяет получить точный результат, если функция f (x) является многочленом до третьей степени включительно.

Таким образом, если на всем промежутке [a,b] эпюра `M_i линейна, а эпюра M_p является квадратичной параболой, интеграл (3.17) можно вычислить по формуле:

D_ip=S(l_k/6EJ_k) {M_p(a_k)× `M<sub>i</sub>(a<sub>k</sub>) +4 M<sub>p</sub>[ (a<sub>k</sub> +b<sub>k</sub>)/2]× `M_i[ (a_k+b_k)/2]+M_p(b_k) × `M_i(b_k) }. (3.21)

При этом однозначности эпюры M_p на промежутке [a,b] не требуется, а формулу можно, конечно, применять и для линейной функции M_p(x).