Вставить чертеж см. листок

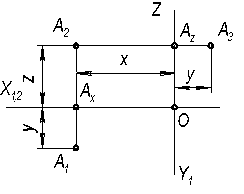
Задача 2Точка задана координатами: А(20, 15, 25). Построить двухкартинный и трёхкартинный комплексные чертежи точки А с осями и без осей, а также её аксонометрию.

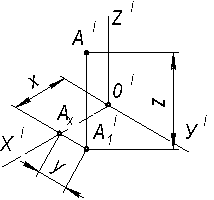
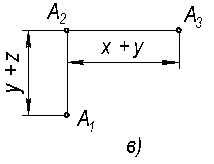
Решение..Через точку Ах проводим вертикальную линию связи и, отложив у, получаем А₁, отложив z, получаем А₂. Через фронтальную проекцию А2 точки А проводим горизонтальную линию связи и, отложив у от точки Аz, получаем профильную проекцию А3 точку А. Обычно точки Ах и Аz на чертеже не указывают. Получим трехкартинный чертеж с осями.. В аксонометрии строим координатную ломанную x-y-z и отмечаем точки А^I₁ и А^I (рис….) Если стоится безосный чертеж, то выбирается, например, положение фронтальной проекции А₂ (рис….). Затем, отложив отрезок (у + z) по вертикальной линии связи и (х + у) по горизонтальной, отмечаем положения горизонталдьной А₁ и профильной А₃ проекций. Часто в работе пользуются двухкартинным чертежом,. Тогда на оси х проекций нужно выбрать начало отсчета 0 (рис….) и построить (А₁ А₂ ), как показано на рисунке …… В таком же безосном чертеже (рисунок ….) координата по оси х может не использоваться.

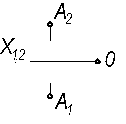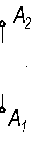Дополнительные задачи

Задача 1Построить комплексный чертёж точек А, В, С, Д, лежащих в биссекторных плоскостях: А и В в чётной и в разных четвертях, С и Д в нечётной и в разных четвертях.

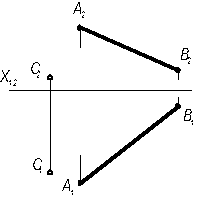
Задача 2Построить следы профильной прямой АВ и указать, через какие четверти пространства она проходит.

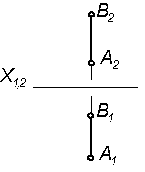
Задача 3Построить комплексный чертёж прямой линии с, проходящей через 4, 1, и 2 четверти. Показать видимость частей прямой и построить точки, принадлежащие прямой с и лежащие: А во 2 четверти, В в 1 четверти и М в 4 четверти.

ТЕМА 2 Комплексный чертеж Монжа

(плоскость)

Вопросы самоконтроля

1. Покажите способы задания плоскости общего и частного положения на комплексном чертеже?

2. Какие плоскости называются плоскостями общего и частного положения?

3. Дайте определение горизонтали и фронтали, линии наибольшего наклона плоскости.

4. Сформулируйте условие принадлежности прямой плоскости.

5. Сформулируйте условие принадлежности точки плоскости.

6. Как через прямую провести проецирующую плоскость?

7. Что называется следом плоскости?

Упражнения

4.1.1 Символической записью дать название плоскостей, способ их задания. Указать их положение относительно плоскостей П₁ и П₂.

а)

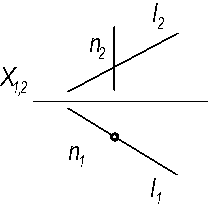
б)

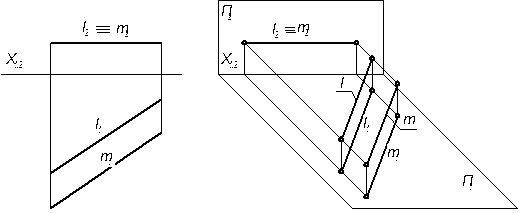в)

	а	б	в
Определитель плоскости
Положение плоскости относительно П1 и П2

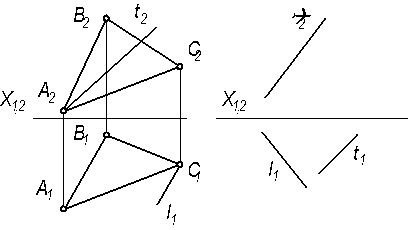
4.1.2 Достроить недостающие проекции прямых t и l,принадлежащих плоскости β(АВС) и α(α₂).

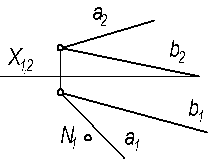
4.1.3 Достроить недостающую проекцию точки N, принадлежащую плоскости α (а∩b).

Задачи

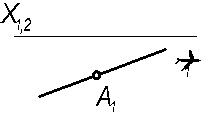
4.2.1 В плоскости Q (Q₁) построить равнобедренный треугольник АВС с основанием АС= 30 мм. Высота треугольника равна 40 мм.

4.2.2 В плоскости Е (АВС) провести горизонталь через точку D и фронталь через точку Е. Построить недостающие проекции точек D и Е.

4.2.3 Через прямую m провести плоскость:

а) горизонтально-проецирующую;

б) общего положения.

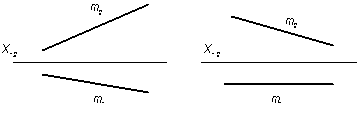
а) б)

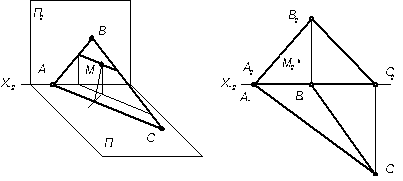
4.2.5 Определить длину пути шарика М, катящегося по плоскости S(АВС), и угол наклона этой плоскости к П₁. Показать решение этой задачи на пространственном чертеже.

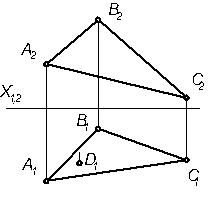
4.2.4 Постройте следы плоскости, заданный двум пересекающимся прямыми АВ и АС. Заданы координаты: А (90; 20; 30), В (70; 10; 60), С (50; 70; 10).

Примеры решения задач:

Задача 1Плоскость задана пересекающимися прямыми: Σ(а∩b). Известна горизонтальная проекция прямой m (m₁ ), лежащей в этой плоскости. Построить фронтальную проекцию этой прямой линии.(рисунок…..)

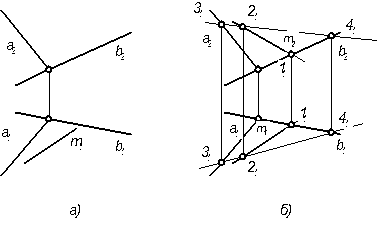
Решение:

Прямая m (рисунок…..), лежащая по условию в плоскости Σ, пересекается прямыми а и b . фронтальные проекции точек пересечения могли бы определить искомую проекцию m₂ Однако точка пересечения прямой m с линией а находится за пределами чертежа, что вынуждает определить вторую точку 2 прямой m с помощью дополнительной прямой линией с (3, 4) плоскости Σ.

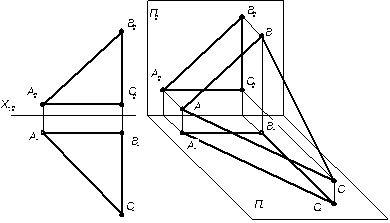
Задача 2Определить углы наклона плоскости α(АВС) к плоскостям проекций П₁ иП₂.

Решение:

Построим 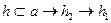(рисунок…..). Через точку В₁ проведем горизонтальную проекцию (В₁ О₁ ) 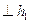линии ската (ВО) и построим ее фронтальную проекцию (В₂О₂).Способом треугольника ∆О₁В₁ В^*определяем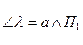

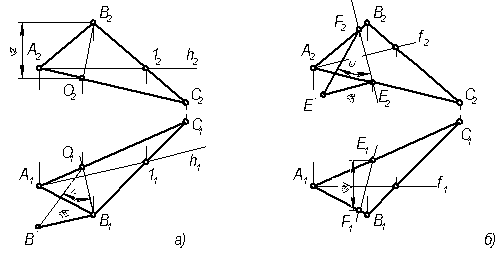
Построим 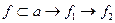(рисунок….) той же плоскости. В произвольном месте построим фронтальную проекцию 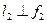линии наибольшего наклона плоскости а к П₂, возьмем на ней отрезок 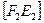и построим горизонтальную проекцию l₁ (F₁ E₁). Способом треугольника через ∆F₂ E₂ E^* и определяем .

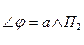Дополнительные задачи

4.4.1 В плоскости Q (АВС) построить произвольный треугольник, стороны которого параллельны плоскостям проекций

4.4.2 Построить недостающую проекцию точки А плоскости

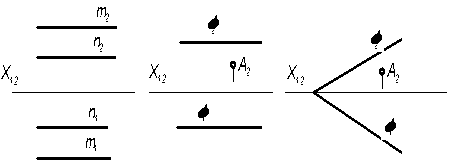4.4.3 . Построить произвольную трехгранную пирамиду, грани которой является плоскостями частного положения, а основание – квадратом.