Мінімізація детермінованих скінчених автоматів

В подальшому при програмуванні скінчених автоматів важливо мати справу з так званими "мінімальними автоматами". Мінімальним для даного скінченого автомата візьмемо еквівалентний йому автомат з мінімальною кількістю станів. Те, що скінчені автомати можна мінімізувати покажемо на наступному прикладі:

c q₅

a, c a, c

q₃ q₄

q₀

a, b

q₂

Мал. 2.

Навіть при поверхневому аналізі діаграми переходів наведеного скінченого автомата видно, що вершини q₃, q₄ та q₅ є "зайвими", тобто при їх вилученні новий автомат буде еквівалентний початковому. З наведеного вище прикладу видно, що для отриманого детермінованого скінченого автомата можна запропонувати еквівалентний йому автомат з меншою кількістю станів, тобто мінімізувати скінчений автомат. Очевидно що серед зайвих станів цього автомата є недосяжні та тупикові стани.

Означення. Стан q скінченого автомата М називається недосяжним, якщо на діаграмі переходів скінченого автомата не існує шляху з q₀ в q.

Алгоритм.Пошук недосяжних станів. Спочатку спробуємо побудувати множину досяжних станів. Якщо Q_m - множина досяжних станів скінченого автомата М, то Q\Q_m - множина недосяжних станів. Побудуємо послідовність множин Q₀, Q₁, Q₂, … таким чином, що:

П0. Q₀ = { q₀ }.

П1. Q₁ = S₀ È { q | q Î d(q₀, a), для всіх а Î S }.

П2. Q_i = S_i-1 È { q | q Î d(q_j, a), q_j Î Q_i-1 та для всіх а Î S }.

……………………….

Пm. Q_m = Q_m+1 = ……..

Очевидно, що кількість кроків П0, П1… скінчена, тому що послідовність Qi монотонна ( Q₀ Í Q₁ Í Q₂ Í …. ) та обмежена зверху - |Q_m| <= |Q|.

Тоді Q_m – множина досяжних станів скінченого автомата, а Q\Q_m – множина недосяжних станів.

Вилучимо з діаграми переходів скінченого автомата М недосяжні вершини. В новому (мінімізованому) автоматі функція d визначається лише для досяжних станів. Побудований нами скінчений автомат з меншою кількістю станів буде еквівалентний початковому.

Означення. Стан q скінченого автомата М називається тупиковим, якщо на діаграмі переходів скінченого автомата не існує шляху з q в F.

Алгоритм.Пошук тупикових станів. Спочатку спробуємо знайти нетупикові стани. Якщо S_m - множина нетупикових станів, то Q\S_m - множина тупикових станів. Побудуємо послідовність множин S₀, S₁, S₂, … таким чином, що:

П0. S₀ = { q | q Î F }.

П1. S₁ = S₀ È { q | d(q, a) S₀ Æ , а Î S }.

П2. S_i = S_i-1 È { q | d(q, a) S_i-1 Æ , а Î S }.

……………………….

Пм. S_m = S_m+1 = ……..

Очевидно, що кількість кроків П0, П1… скінчена, тому що послідовність S_i монотонна ( S₀ Í S₁ Í S₂ Í …. ) та обмежена зверху - |S_m| <= |Q|.

Тоді S_m – множина нетупикових станів скінченого автомата, а Q\S_m – множина тупикових станів. В новому (мінімізованому) автоматі функція d визначається лише для нетупикових станів.

В прикладі наведеному на Мал. 2 множина недосяжних станів - {q₅}, а множина тупикових станів - {q₃, q₄}. Таким чином, для вище наведеного скінченого автомата еквівалентний йому автомат з меншою кількістю станів буде:

a, b

q₀ q₂

Мал. 3.

Автомат, у котрого відсутні недосяжні та тупикові стани, піддається подальшій мінімізації шляхом “склеювання” еквівалентних станів. Продемонструємо це на конкретному прикладі:

a, c

c

b

q₁ q₂

c a, c

q₀ a

q₃ q₄

Мал. 4.

Очевидно, що для наведеного вище скінченого автомата можна побудувати еквівалентний йому скінчений автомат з меншою кількістю станів:

a, b c a, c

q₀ q₁ q₂

Мал. 5.

Ми досягли бажаного нам результату шляхом “склеювання” двох станів q₁, q₃. та q₂, q₄.

Означення. Два стани q₁ та q₂ скінченого автомата М називаються еквівалентними, якщо множини слів, які розпізнає автомат, починаючи з q₁ та q₂, співпадають.

Нехай q₁ та q₂ два різних стани скінченого автомата М, а х Î S*. Будемо говорити, що ланцюжок х розрізняє стани q₁ та q₂, якщо (q₁,x) |=* (q₃, e) та (q₂,x) |=* (q₄, e), причому один з станів q₃ або q₄ не належить множині заключних станів. Стани q₁ та q₂ називаються k – нерозрізнені, якщо не існує ланцюжка х (|x| <=k), що розрізняє стани q₁ та q₂. Два стани q₁ та q₂ нерозрізнені, якщо вони

к-нерозрізнені для довільного к.

Твердження: два стани q₁ та q₂ довільного скінченого автомата М з n станами нерозрізнені, якщо вони (n-2)-нерозрізнені.

Доведення: На першому кроці розіб’ємо множину станів скінченого автомата на дві підмножини: F та Q\F. На цій основі побудуємо відношення º⁰:

q₁ º⁰ q₂ , якщо обидва стани одночасно належать F або Q\F.

Побудуємо відношення º^к :

q₁ º^к q₂ , якщо q₁ º^к-1 q₂ та d( q₁, а) º^к-1 d( q₂, а) для всіх а Î S.

Очевидно, кожна побудована множина містить не більше (n-1) елементи. Таким чином, можна отримати не більше (n-2) уточнення відношення º⁰ .

Відношення º^n-2 визначає класи еквівалентних станів автомата М.

Алгоритм. Побудова мінімального скінченого автомата.

П1. Побудувати скінчений автомат без тупикових станів.

П2. Побудувати скінчений автомат без недосяжних станів.

П3. Знайти множини еквівалентних станів та побудувати найменший (мінімальний) автомат.

Ознайомившись з деякими результатами теорії скінчених автоматів, спробуємо уяснити, які мови (словарні множини) є скінченоавтоматними.

Твердження: Скінчено автоматними є наступні множини:

- порожня словарна множина - Æ;

- словарна множина, що складається з одного e-слова – {e};

- множина {a}, a Î S.

Доведення: в кожному випадку нам доведеться конструктивно побудувати відповідний скінчений автомат:

1. Довільний скінчений автомат з пустою множиною заключних станів (а мінімальний – з пустою множиною станів) допускає Æ;

2. Розглянемо автомат М =<{q₀}, S, q0, d, {q0}>, у якому d не визначено ні для яких а Î S.

Тоді L(M) = {e}.

3. Розглянемо автомат М =<{q₀, q₁}, S, q₀, d, {q₁}>, у якому функція d визначена лише для пари (q₀, a), а саме: d(q₀, a) = q₁.

Тоді L(M) = {a}.

Твердження: Якщо М₁ = <Q₁, S, q₀₁, d₁, F₁> та М₂ = <Q₂, S, q₀₂, d₂, F₂>, що визначають відповідно мови L(M₁) та L(M₂), то скінченоавтоматними мовами будуть:

- L(M₁) È L(M₂);

- L(M₁) * L(M₂);

- {L(M₁)} = {e} È L(M₁) È L(M₁)* L(M₁) È ….,

де:

L(M₁) È L(M₂) = { w | w Î L(M₁) або w Î L(M₂) },

L(M₁) * L(M₂) = {w=xy | x Î L(M₁), y Î L(M₂) }.

Доведення:

1. Побудуємо автомат М = <Q, S, q₀, d, F>, такий що L(M) = L(M₁) È L(M₂).

- Q = Q₁ È Q₂ È {q₀}, де q₀ – новий стан (q₀ Ï Q₁ È Q₂);

- Функцію d визначимо таким чином:

d(q,a) = d₁(q,a), q Î Q₁, а Î S;

d(q,a) = d₂(q,a), q Î Q₂, а Î S;

d(q₀,a) = d1(q₀₁,a) È d2(q₀₂,a), q₀₁ Î Q₁, q₀₂ Î Q₂, а Î S;

- Множина заключних станів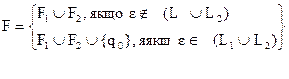

Побудований в цьому випадку автомат взагалі недетермінований. Індукцією по i >=1 покажемо, що (q₀,w) |=ⁱ (q,e) можливо тоді і тільки тоді, коли (q₀₁,w) |=ⁱ (q,e), q Î F₁ або (q₀₂,w) |=ⁱ (q,e), q Î F₂.

2. Побудуємо автомат М = <Q, S, q₀, d, F>, такий що L(M) = L(M₁) * L(M₂):

- Q = Q₁ È Q₂ ;

- q₀ =q₀₁;

- Функцію d визначимо таким чином:

d(q,a) = d₁(q,a), q Î Q₁\F₁, а Î S;

d(q,a) = d₂(q,a), q Î Q₂, а Î S;

d(q,a) = d₁(q,a) È d₂(q₀₂,a), q Î F₁, q₀₂ Î Q₂,а Î S;

- Множина заключних станів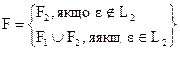

3. Побудуємо автомат М = <Q, S, q₀, d, F>, такий що L(M) = {L(M₁)}:

- Q = Q₁ È {q₀}, де q₀ – новий стан (q₀ Ï Q1);

- Функцію d визначимо таким чином:

d(q,a) = d₁(q,a), q Î Q₁\F₁, а Î S;

d(q₀,a) = d₁(q₀₁,a) , q₀₁ Î Q₁, а Î S;

d(q,a) = d₁(q,a) È d₁(q₀₁,a), q Î F₁, а Î S;

- Множина заключних станів F = F₁ È {q₀}.