Уравнение Бернулли. Статическое и динамическое давления

ГОСУДАРСТВЕННЫЙ МЕДИЦИНСКИЙ УНИВЕРСИТЕТ г. СЕМЕЙ

Методическое пособие по теме:

Исследование реологических свойств биологических жидкостей.

Методы исследования кровообращения.

Реография.

Составитель: Преподаватель

Ковалева Л.В.

Основные вопросы темы:

1. Уравнение Бернулли. Статическое и динамическое давления.
2. Реологические свойства крови. Вязкость.
3. Формула Ньютона.
4. Число Рейнольдса.
5. Ньютоновская и Неньютоновская жидкость
6. Ламинарное течение.
7. Турбулентное течение.
8. Определение вязкости крови с помощью медицинского вискозиметра.
9. Закон Пуазейля.
10. Определение скорости кровотока.
11. Полное сопротивление тканей организма. Физические основы реографии. Реоэнцефалография
12. Физические основы баллистокардиографии.

Уравнение Бернулли. Статическое и динамическое давления.

Идеальной называется несжимаемая и не имеющая внутреннего трения, или вязкости; стационарным или установившимся называется течение, при котором скорости частиц жидкости в каждой точке потока со временем не изменяются. Установившееся течение характеризуют линиями тока - воображаемыми линиями, совпадающими с траекториями частиц. Часть потока жидкости, ограниченная со всех сторон линиями тока, образует трубку тока или струю. Выделим трубку тока настолько узкую, что скорости частиц V в любом ее сечении S, перпендикулярном оси трубки, можно считать одинаковыми по всему сечению. Тогда объем жидкости, протекающий через любое сечение трубки в единицу времени остается постоянным, так как движение частиц в жидкости происходит только вдоль оси трубки: . Это соотношение назы­вается условием неразрывности струи. Отсюда следует, что и для реальной жидкости при установившемся течении по трубе переменного сечения количество Qжидкости, проте­кающее в единицу времени через любое сечение трубы, остается по­стоянным (Q = const) и средние скорости течения в различных сече­ниях трубы обратно пропорциональны площадям этих сечений: и т . д.

Выделим в потоке идеальной жидкости трубку тока, а в ней — достаточно малый объем жидкости массой , который при тече­нии жидкости перемещается из положения А в положение В.

Из-за малости объема можно считать, что все частицы жидкости в нем находятся в равных условиях: в положе­нии А имеют давление скорость и находятся на высоте h₁от нуле­вого уровня; в положении В — соот­ветственно . Сечения трубки тока соответственно S₁ и S₂.

Жидкость, находящаяся под дав­лением, обладает внутренней потен­циальной энергией (энергией давле­ния), за счет которой она может совершать работу. Этаэнергия W_p измеряется произведением давления на объем V жидкости: . В данном случае перемещение массы жидкости происходит под действием разности сил давления в се­чениях Si и S₂. Совершаемая при этом работа А_р равняется разности по­тенциальных энергий давления в точках . Эта работа расходуется на работу по преодолению действия силы тяжес­ти и на изменение кинетической энергии массы

жидкости:

Следовательно, А_р = A_h + A_D

Перегруппировав члены уравнения, получим

Положения А и В выбраны произвольно, поэтому можно утверждать, что в любом месте вдоль трубки тока сохраняется условие

разделив это уравнение на , получим

где — плотность жидкости.

Это и есть уравнение Бернулли. Все члены уравнения, как легко убедиться, имеют размерность давления и называются: статистическим: гидростатическим: - динамическим. Тогда уравнение Бернулли можно сформулировать так:

при стационарном течении идеальной жидкости полное давление равное сумме статического, гидростатического и динамического давлений, остается величиной постоянной в любом поперечном сечении потока.

Для горизонтальной трубки тока гидростатическое давление ос­тается постоянным и может быть отнесено в правую часть уравнения, которое при этом принимает вид

статистическое давление обусловливает потенциальную энергию жидкос­ти (энергию давления), динамическое давление — кинетическую.

Из этого уравнения следует вывод, называемый правилом Бернулли:

статическое давление невязкой жидкости при течении по горизон­тальной трубе возрастает там, где скорость ее уменьшается, и на­оборот.

Вязкость жидкости

Реология- это наука о деформациях и текучести вещества. Под реологией крови (гемореологией) будем понимать изучение биофизических особенностей крови как вязкой жидкости. В реальной жидкости между молекулами действуют силы взаимного притяжения, обусловливающие внутреннее трение. Внутреннее трение, например, вызывает силу сопротивления при помешивании жидкости, замедление скорости падения брошенных в нее тел, а также при определенных условиях — ламинарное течение.

Ньютон установил, что сила F_Bвнутреннего трения между двумя слоями жидкости, движущимися с различными скоростями, зависит от природы жидкости и прямо пропорциональна площади S соприкасающихся слоев и градиенту скорости dv/dz между ними F = 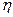Sdv/dz где 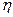— коэффициент пропорциональности, называемый коэффициентом вязкостиили просто вязкостью жидкости и зависящий от ее при­роды.

Сила F_B действует касательно к поверхности соприкасающихся слоев жидкости и направлена так, что ускоряет слой, движущийся более медленно, замедляет слой, движущийся бо­лее быстро.

Градиент скорости в данном случае характери­зует быстроту изменения скорости между слоями жидкости, т. е. в направ­лении, перпендикулярном направлению течения жид­кости. Для конечных зна­чений он равен .

Единица коэффициента вязкости в ,в системе СГС - , эта единица называется пуазом (П). Соот­ношение между ними: .

На практике вязкость жидкости характеризуют относительной вязкостью , под которой понимают отношение коэффициента вяз­кости данной жидкости 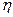к коэффициенту вязкости воды при той же температуре:

У большинства жидкостей (вода, низкомолекулярные органические соединения, истинные растворы, расплавленные металлы и их соли) коэффициент вязкости зависит только от природы жидкости и темпе­ратуры (с повышением температуры коэффициент вязкости понижа­ется). Такие жидкости называются ньютоновскими.

У некоторых жидкостей, преимущественно высокомолекулярных (например, растворы полимеров) или представляющих дисперсные системы (суспензии и эмульсии), коэффициент вязкости зависит также от режима течения — давления и градиента скорости. При их увеличе­нии вязкость жидкости уменьшается вследствие нарушения внутренней структуры потока жидкости. Такие жидкости называются структурно вязкими или неньютоновскими. Их вязкость характеризуют так называемым условным коэффициентом вязкости, который относится к определенным условиям течения жидкости (давление, скорость).

Кровь представляет собой суспензию форменных элементов в бел­ковом растворе — плазме. Плазма – практически ньютоновская жидкость. Поскольку 93 % форменных элементов составляют эритроциты, то при упрощенном рассмотрении кровь – это суспензия эритроцитов в физиологическом растворе. Поэтому, строго говоря, кровь должна быть отнесена к неньютоновским жидкостям. Кроме того, при течении крови по сосудам наблюдается концентрация форменных элементов в цент­ральной части потока, где вязкость соответственно увеличивается. Но поскольку вязкость крови не так велика, этими явлениями пренебре­гают и считают ее коэффициент вязкости постоянной величиной.

Относительная вязкость крови в норме составляет 4,2—6. При патоло­гических условиях она может снижаться до 2—3 (при анемии) или повы­шаться до 15—20 (при полицитемии), что сказывается на скорости оседания эритроцитов (СОЭ). Изменение вязкости крови - одна из причин изменения скорости оседания эритроцитов (СОЭ). Вязкость крови имеет диагностическое значение. Некоторые инфекционные заболевания увеличивают вязкость, другие же, например брюшной тиф и туберкулез, - уменьшают.

Относительная вязкость сыво­ротки крови в норме 1,64—1,69 и при патологии 1,5—2,0. Как и у любой жидкости, вязкость крови возрастает при снижении температуры. При повышении жесткости эритроцитарной мембраны, например при атеросклерозе, вязкость крови также возрастает, что приводит к увеличению нагрузки на сердце. Вязкость крови неодинакова в широких и узких сосудах, причем влияние диаметра кровеносного сосуда на вязкость начинает сказываться при просвете менее 1 мм. В сосудах тоньше 0,5 мм вязкость уменьшается прямо пропорционально укорочению диаметра, поскольку в них эритроциты выстраиваются вдоль оси в цепочку наподобие змейки и окружены слоем плазмы, изолирующей «змейку» от сосудистой стенки.