Определение коэффициента теплопроводности калориметрическим методом

Цел работы:определить коэффициент тепловодности металла.

Приборы и принадлежности: два калоритметрических сосуда соединенных друг с другом испытательным стержнем закрытым с наружной стороны асбестом. Термометры и электроплитка.

Теоретическое введение

Теплопроводность, обусловлена переносом энергии, является одним из трех существующих в природе явлений переноса. Теплопроводностью обладают все вещества: газы, жидкости и твердые тела. В твердых телах в отличии от газов и жидкостей невозможна конвекция, поэтому перенос тепла осуществляется только теплопроводностью.

Теплота в твердых телах передается колебаниями кристаллической решеткой. Если при данной температуре 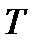один из узлов решетки колеблется с амплитудой 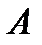, то он будучи связан со своими соседями, будет действовать на них, вызывая увелечение амплитуды колебаний этих соседних частиц. Таким образом энергия тепловых колебаний передается от одного узла решетки к другому посредством установления волнового процесса.

В металлах в отличии от диэлектриков перенос теплоты осуществляется не только кристаллической решеткой, но и свободными электронами. Поэтому теплопроводность металлов 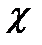в общем случае складывается из теплопроводности решетки 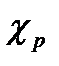и теплопроводности 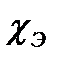, обусловленой свободными электронами: 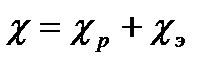. Металлы отличается хорошей теплопроводностью, которая осуществляется в основном за счет переноса энергии свободными электронами т.е. 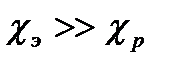и поэтому .

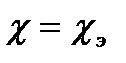Теплопроводность имеет место тогда, когда концы металлического стержня поддерживаются при разных температурах. При этом в стержне возникает непрерывный поток теплоты. Каждый узел (ион) колеблется с меньшей амплитудой, чем соседний с ним со стороны более нагретого конца, и с большей амплитудой, чем соседней с ним со стороны менее нагретого конца, и с большей амплитудой.

Количественно тепловой поток 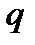через поперечное сечение стержня 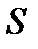при градиенте температуры 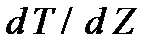можно рассчитать по известной формуле Фурье:

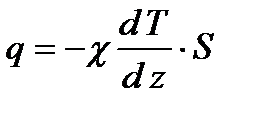(1)

Коэффициент пропорциональности 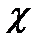в этой формуле есть коэффициент теплопроводности. Он численно равняется количеству тепла, прошедшего через единицу площади за единицу времени при градиенте температуры, равному единице (площадка 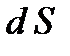перпендикулярна оси 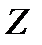). 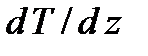– градиент температуры, равный скорости изменения температуры на единицу длины в направлении нормали к площадке 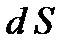. Знак минус в формуле (1) показывает, что энергия переносится в сторону убывания температуры. В связи с чем знак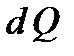и и 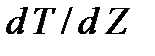, противоположны. В системе 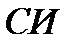коэффициент теплопроводности измеряется 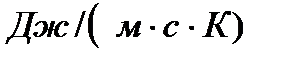или в ваттах на метр кельвин 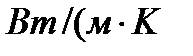). Экспериментальную формулу теплового потока (1) можно вычислить из молекулярно- кинетической теории. По этой теории свободные электроны в метталлах рассматриваются как электронный газ, частицы которого обладают тремя степенями свободы, т.е. ведут себя как одноатомный газ, и их движение подчиняется всем законам идеального газа. Если температура ( металла) газа 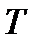в разных местах различна, то и средняя энергия электрона также будет различной. Перемещаясь вследствии теплового движения из одних мест в другие, электроны переносят запасенную ими энергию, что и обуславливает процесс теплопроводности.

Формула теплового потока полученная из молекулярно- кинетической теории полностью совпадает с уравнением (1). При этом получается выражение для коэффициента теплопроводности металлов:

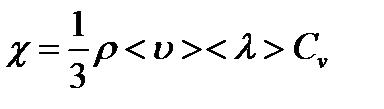(2)

Здесь 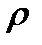– плотность газа, 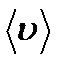– средняя скорость теплового движения электрона, 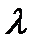- средняя длина свободного пробега электрона, 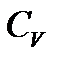- удельная теплоемкость электронного газа постоянном объеме.