Моделирование процесса квантования по времени
Для изучения способа квантования по времени необходимо составить S-модель, приведенную на рис. 1.8. Блок экстраполятора нулевого порядка Zero-Order Hold выполняет дискретизацию входного сигнала по времени. Параметр Sample time – величина шага дискретизации по времени.
Выполните дискретизацию по времени с различным шагом (табл. 1.3) и сделайте вывод о его влиянии на отклонение квантованного сигнала от исходного.
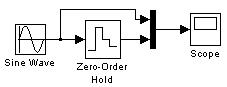
Рис. 1.8. Схема S-модели для исследования АИ-модулятора
Таблица вариантов 1.3
| № вар. | Sample time | № вар. | Sample time |
| 0,5; 0,25 | 1,2; 0,6 | ||
| 0,7; 0,35 | 0,5; 0,25 | ||
| 0,8; 0,4 | 1,3; 0,65 | ||
| 0,4; 0,2 | 0,7; 0,35 | ||
| 0,9; 0,45 | 1,1; 0,55 | ||
| 0,6; 1,3 | 0,8; 0,4 | ||
| 1,0; 0,5 | 0,4; 0,2 | ||
| 1,1; 0,55 | 0,9; 0,45 | ||
| 1,2; 0,6 | 0,6; 1,3 | ||
| 1,3; 0,65 | 1,0; 0,5 |
Моделирование кодо-импульсной модуляции
Для изучения кодо-импульсной модуляции необходимо составить S-модель, приведенную на рис. 1.9. Блоки Uniform Encoder (АЦП) и Uniform Decoder (ЦАП) – цифровые элементы. Для проведения исследований необходимо выбрать разрядность АЦП и ЦАП – параметр bits в соответствии с вариантом (табл. 1.4). Сделайте вывод о влиянии разрядности цифровых элементов на отклонение квантованного сигнала от исходного.
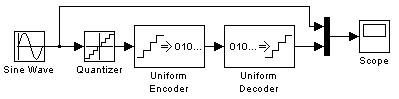
Рис. 1.9. Схема S-модели для изучения кодо-импульсной модуляции
Таблица вариантов 1.4
| № вар. | bits | № вар. | bits | № вар. | bits | № вар. | bits |
| 3; 4 | 6; 8 | 8; 10 | 3; 9 | ||||
| 2; 3 | 2; 3 | 9; 12 | 7; 9 | ||||
| 5; 7 | 4; 8 | 5; 8 | 9; 12 | ||||
| 7; 9 | 5; 7 | 3; 9 | 3; 4 | ||||
| 6; 8 | 5; 8 | 4; 8 | 2; 5 |
Контрольные вопросы
1. Какие системы автоматического управления относят к дискретным?
2. Как осуществляется дискретизация непрерывного сигнала?
3. Что такое решетчатая функция?
4. Что называется квантованием? Перечислите и дайте определение способам квантования и соответствующим АСУ.
5. Что называется модуляцией?
6. Какой вид модуляции лежит в основе импульсных АСУ?
7. Какой вид модуляции лежит в основе цифровых АСУ?
8. Опишите структуру релейной и импульсной АСУ.
9. С помощью какого блока пакета Simulink может быть реализован процесс квантования по уровню?
10. С помощью каких блоков пакета Simulink может быть реализован процесс дискретизации по времени?
Лабораторная работа №2
Решение разностных уравнений
Цель работы – освоение методов решения линейных разностных уравнений для исследования дискретных систем
КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Линейное однородное разностное уравнение второго порядка с постоянными коэффициентами имеет вид
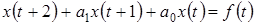 . (2.1)
. (2.1)
Чтобы подчеркнуть дискретный характер изменения времени, это уравнение часто записывают в форме
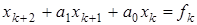 . (2.2)
. (2.2)
Разностные уравнения третьего и более высоких порядков записываются аналогично. Известны два основных метода решения линейных разностных уравнений – с помощью характеристического полинома и с использованием z-преобразования, аналогичного преобразованию Лапласа.
1.1. Решение разностных уравнений с помощью
