Порядок выполнения работы и обработка результатов. Задачей работы является моделирование критического состояния реактора, т.е

Задачей работы является моделирование критического состояния реактора, т.е. необходимо добиться выполнения критических условий при постоянном по активной зоне коэффициента размножения. Задача решается на модели методом последовательных приближений.

1. Вначале задают произвольное распределение величин источников 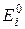в активной зоне. Установка нужного значения E_i производится с помощью потенциометра R_рег (рис.2а). Питание всех узлов производится от общего источника питания. Нужно учитывать, что при регулировкеE_i в некотором узле перераспределение потенциалов в сетке может привести к изменению уже установленных величин E_i и токов в соседних узлах.

2. Снимают распределение потоков тепловых нейтронов, т.е. распределение 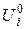(нижний индекс означает номер итерации).

3. Определяются местные значения коэффициента размножения k_i в каждой узловой точке по выражению (19):

.

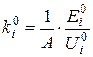4.определяется среднее значение коэффициента размножения в активной зоне:

,

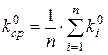где n – число узловых точек в активной зоне.

5. Вычисляется и устанавливается на модели новое, улучшенное распределение источников. Величина источника в точке должна быть пропорциональна величине потока тепловых нейтронов в этой точке:

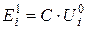
Величина коэффициента выбирается так, чтобы наиболее удобно нормировать кривую распределения, например так, чтобы величина E_i в центре активной зоны (E₈) не менялась от итерации к итерации. В последующих итерациях величина С приближается к величине f.

6. Снимается улучшенное распределение потока тепловых нейтронов .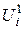

Далее описанный в пп 1¸6 цикл повторяется. В каждом новом цикле для задания источников 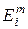используется значение 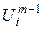, полученное в предыдущем цикле. Процесс повторяется до тех пор, пока коэффициент размножения не станет одинаковым (с определенной точностью ) во всех точках i активной зоныи пока он не перестанет меняться от итерации к итерации.

7. Снимают также распределение потока тепловых нейтронов в отражателе и быстрых нейтронов V_iво всем реакторе.

Описанный итерационный процесс имитирует реальный непрерывный во времени процесс установления стационарного распределения нейтронных потоков в критическом реакторе. Итерационный процесс быстро сходится: обычно для решения требуется 4¸5 итераций. В результате решения получают критический коэффициент размножения и распределения быстрых и тепловых нейтронов в ректоре.

8. Результаты измерения заносятся в таблицу

№ итерации	Величины	Номера узловых точек	Примечание
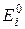											С =
=
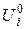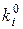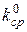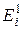											С =
=
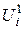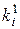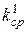	. . .										С =
. . .

9. Строятся графики распределения потоков быстрых и тепловых нейтронов в критическом реакторе. Графики строятся в относительных единицах. При построении необходимо учесть масштабный множитель .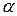

10. Составляется отчет о работе, который должен включать следующее:

– кратко необходимые теоретические сведения и соотношения;

– результаты итерационного определения величин потоков быстрых и тепловых нейтронов в активной зоне, а также расчеты значений местных и средних коэффициентов размножения;

– результаты определения окончательных распределений потоков быстрых и тепловых нейтронов в активной зоне и отражателе;

– графики распределения потоков быстрых и тепловых нейтронов в критическом реакторе;

– аргументированные выводы по работе.

Литература

1. Ганев И.Х. Физика и расчет реактора. – М.: Энергоатомиздат, 1981

2. Волынский Б., Бухман В. Модели для решения краевых задач. – М.: ГИФМЛ, 1960

3. Карплюс У. Моделирующие устройства для решения задач теории поля.–М.:ИЛ, 1962

Контрольные вопросы и задания

1. Записать двухгрупповые уравнения и сформулировать граничные условия для плоского реактора.

2. Область применимости диффузионного приближения.

3. Как производится конечно-разностные преобразования уравнений диффузии?

4. Как получить условия моделирования для сеточной модели ректора.

5. В чем состоит метод последовательных приближений при моделировании стационарного распределения нейтронного потока в реакторе?

6. Что является критерием сходимости итерации при решении задачи на модели?

7. Задача о гомогенном ядерном реакторе с отражателем в двухгрупповом приближении.

8. Как распределены потоки быстрых и тепловых нейтронов в активной зоне и отражателе?

9. Чем объясняется всплеск в распределении потока тепловых нейтронов в отражателе?

10. На каком расстоянии от активной зоны всплеск в распределении потока тепловых нейтронов в отражателе примерно расположен?

11. Может ли максимум потока тепловых нейтронов в отражателе превышать максимальное значение потока тепловых нейтронов в активной зоне?

12. Что такое жесткость спектра?

13. В каком ядерном реакторе на тепловых нейтронах спектр жестче?

14. Физический смысл эффективной добавки за счет отражателя в двухгрупповом приближении.

15. Условие критичности гомогенного ядерного реактора с отражателем в двухгрупповом приближении.

16. Методы определения критических параметров ядерного реактора с отражателем в двухгрупповом приближении.

17. Распределение потоков нейтронов в гомогенном ядерном реакторе с отражателем в одно- и двухгрупповом приближении.

18. Определить в двухгрупповом приближении критический объем сферического гомогенного реактора без отражателя. Ядерное топливо – чистый уран-235, замедлитель – тяжелая вода.