Пециальная теория относительности.
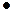 При движении инерциальной системы отсчёта К¢ относительно инерциальной системы отсчёта К в направлении совпадающих осей х и х¢ cо скоростью V выполняются преобразования координат и времени Лоренца:
При движении инерциальной системы отсчёта К¢ относительно инерциальной системы отсчёта К в направлении совпадающих осей х и х¢ cо скоростью V выполняются преобразования координат и времени Лоренца:
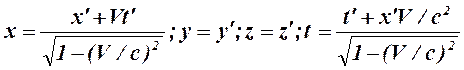 |
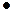 Обратные преобразования от системы К к системе К¢:
Обратные преобразования от системы К к системе К¢:
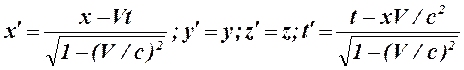 |
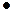
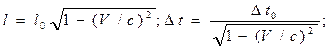
Лоренцово преобразование длины и промежутков времени:
где l0 – собственная длина, Δt0 – собственное время.
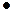 Инвариантность интервала ΔS между событиями:
Инвариантность интервала ΔS между событиями:
 |
 Преобразование скорости при переходе от системы К΄ к системе К :
Преобразование скорости при переходе от системы К΄ к системе К :
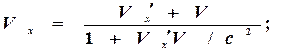 |
 Релятивистское уравнение динамики частицы:
Релятивистское уравнение динамики частицы:
 |
 Полная и кинетическая энергия релятивистской частицы:
Полная и кинетическая энергия релятивистской частицы:
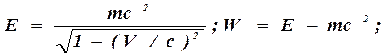 |
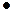
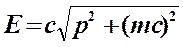 |
Связь между энергией и импульсом релятивистской частицы:
В этих формулах m– масса покоя, в старых учебниках её обозначают m0.
еханика жидкостей и газов.
 В стационарном потоке идеальной жидкости вдоль любой линии тока имеет место уравнение Бернулли :
В стационарном потоке идеальной жидкости вдоль любой линии тока имеет место уравнение Бернулли :
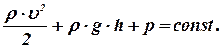
Здесь 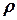 - плотность жидкости,
- плотность жидкости, 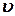 - скорость движения жидкости в данном сечении трубы,
- скорость движения жидкости в данном сечении трубы, 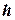 - высота сечения трубы над некоторым уровнем,
- высота сечения трубы над некоторым уровнем, 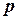 - давление.
- давление.
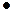 Скорость вытекания жидкости из малого отверстия равна
Скорость вытекания жидкости из малого отверстия равна 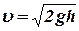 , где
, где 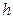 - высота поверхности жидкости над отверстием.
- высота поверхности жидкости над отверстием.
• Через любое поперечное сечение трубы за равные промежутки времени проходят равные объемы жидкости, поэтому 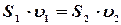 , где:
, где: 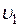 и
и 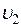 — скорости жидкости в двух сечениях трубы площадью
— скорости жидкости в двух сечениях трубы площадью 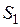 и
и 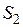 .
.
• Сила сопротивления движению шарика радиусом r в вязкой жидкости (или в газе)
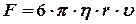 ,
,
где 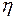 — коэффициент внутреннего трения жидкости или газа (динамическая вязкость),
— коэффициент внутреннего трения жидкости или газа (динамическая вязкость), 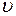 — скорость шарика.
— скорость шарика.
• Поток жидкости через поперечное сечение трубы определяется формулой Пуазейля:
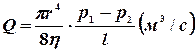 ,
,
где 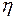 — динамическая вязкость жидкости (газа), Rи l— радиус и длина трубы,
— динамическая вязкость жидкости (газа), Rи l— радиус и длина трубы, 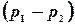 — разность давлений на её концах.
— разность давлений на её концах.
римеры решения задач.
Задача 1.
Сплошной цилиндр массой m=10 кг и радиусом R=0.5 м, раскрученный до частоты n=5 об/с, кладут в угол комнаты, при этом он вращается на месте. Коэффициент трения между цилиндром и полом 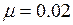 . Трением между цилиндром и стеной пренебречь. Определить угловое ускорение цилиндра, число оборотов до его полной остановки и работу сил трения.
. Трением между цилиндром и стеной пренебречь. Определить угловое ускорение цилиндра, число оборотов до его полной остановки и работу сил трения.
Решение
Y


 | |||
 |

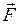
X
На рисунке изображены цилиндр и силы, действующие на него:
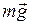 - сила тяжести;
- сила тяжести;
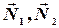 - силы реакции со стороны пола и стены соответственно;
- силы реакции со стороны пола и стены соответственно;
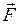 - сила трения;
- сила трения;
О - ось вращения цилиндра.
Центр масс тела неподвижен; II закон Ньютона в проекции на вертикальную и горизонтальную оси:
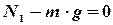
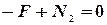
Кроме того, 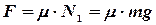
Основной закон динамики вращательного движения твёрдого тела относительно оси вращения О:
 ,
,
где 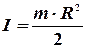 - момент инерции цилиндра, следовательно,
- момент инерции цилиндра, следовательно,
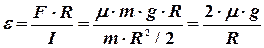
Для определения числа оборотов необходимо определить угол поворота 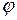 цилиндра вокруг своей оси до его полной остановки. С этой целью используются формулы кинематики:
цилиндра вокруг своей оси до его полной остановки. С этой целью используются формулы кинематики:
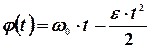
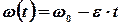
Знак минус соответствует равнозамедленному движению.
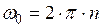 - начальная угловая скорость.
- начальная угловая скорость.
Учитывая, что в момент остановки 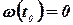 , получаем:
, получаем: 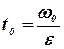
и






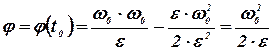
Время, необходимое для остановки
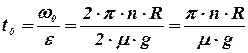
Число оборотов цилиндра
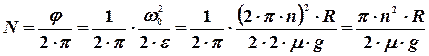
Определим теперь работу силы трения до остановки цилиндра, которая есть произведение силы 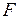 на 2π R N-перемещение точки, к которой приложена сила (сила трения направлена против направления перемещения, поэтому ее работа отрицательна):
на 2π R N-перемещение точки, к которой приложена сила (сила трения направлена против направления перемещения, поэтому ее работа отрицательна):
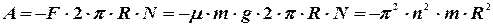
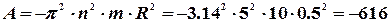 Дж
Дж
Это же значение работы можно определить из других соображений : работа сил трения равна изменению кинетической энергии тела
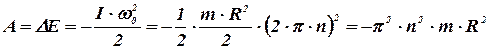
Проведём вычисления :
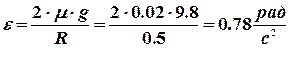
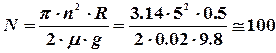 оборотов.
оборотов.
Задача 2.
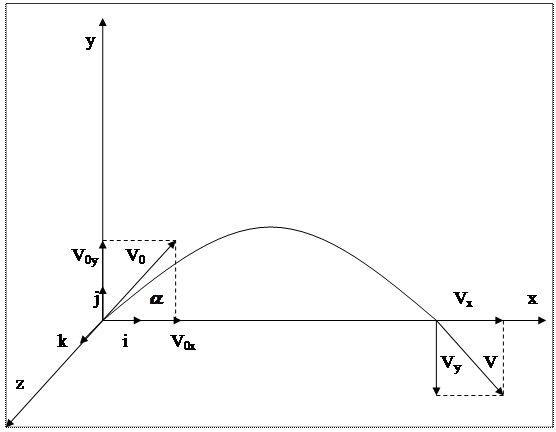
Тело массой 3 кг брошено с начальной скоростью 20 м/с под углом 300 к горизонту. Определить момент импульса тела в конце траектории относительно точки бросания.
Решение.
Момент импульса равен 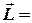 [
[  ], где
], где 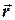 -радиус-вектор тела, а
-радиус-вектор тела, а 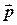 - его импульс. В декартовых координатах
- его импульс. В декартовых координатах 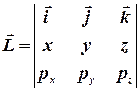 , где
, где 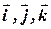 - единичные векторы, направленные по осям x,y,z- соответственно. Выберем декартову систему координат так, чтобы ее центр находился в точке бросания, а вектор начальной скорости тела - в плоскости xy, тогда траектория тела будет тоже находиться в плоскости xy.
- единичные векторы, направленные по осям x,y,z- соответственно. Выберем декартову систему координат так, чтобы ее центр находился в точке бросания, а вектор начальной скорости тела - в плоскости xy, тогда траектория тела будет тоже находиться в плоскости xy.
В момент падения тела координата x равна дальности полёта: 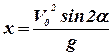 , координаты y и z равны нулю: y=0, z=0, проекция скорости тела на ось x равна: Vx=V0 cosα, проекция скорости тела на ось y равна: Vy=-V0 sinα, проекция скорости тела на ось z равна: Vz=0.
, координаты y и z равны нулю: y=0, z=0, проекция скорости тела на ось x равна: Vx=V0 cosα, проекция скорости тела на ось y равна: Vy=-V0 sinα, проекция скорости тела на ось z равна: Vz=0.
Тогда
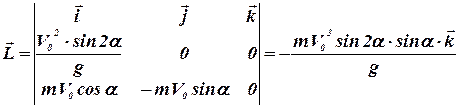 .
.
Следовательно, момент импульса тела в момент падения направлен против оси z и равен по модулю 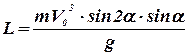 =
= 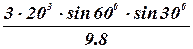 кг м2/c = 2.12 103 кг м2/c.
кг м2/c = 2.12 103 кг м2/c.
Задачу можно решить и не используя формулу для момента импульса материальной точки в декартовых координатах.
Модуль момента импульса материальной точки равен :
L = r mV sinα, где r- модуль радиуса-вектора материальной точки в конце полета, равный дальности полета: 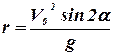 , V-модуль скорости тела в конце полета, V = V0, так как известно, что скорость в конце полета по модулю равна скорости в его начале, α –угол между вектором скорости и радиус-вектором материальной точки в конце полета, он равен углу α между осью х и вектором начальной скорости V0.
, V-модуль скорости тела в конце полета, V = V0, так как известно, что скорость в конце полета по модулю равна скорости в его начале, α –угол между вектором скорости и радиус-вектором материальной точки в конце полета, он равен углу α между осью х и вектором начальной скорости V0.
Подставляя, получим что, момент импульса тела L = r mV sinα в момент падения равен: 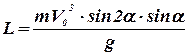 =
= 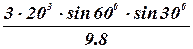 кг м2/c = 2.12 103 кг м2/c.
кг м2/c = 2.12 103 кг м2/c.
Задача 3.
Шар, радиус которого R = 5 см, подвешен на невесомой нити длиной l0 = 10 см. Определить относительную погрешность, которую допускают, если, вычисляя период колебаний такого маятника, принимают его за математический маятник длиной l = 15 см.
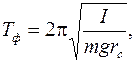 Решение. Шар, висящий на нити, представляет собой физический маятник. Его период колебаний Tф выражается формулой:
Решение. Шар, висящий на нити, представляет собой физический маятник. Его период колебаний Tф выражается формулой:
(1)
где I–момент инерции маятника относительно оси, проходящей через точку подвеса, m –масса маятника, rc – расстояние от центра масс до точки подвеса и g –ускорение свободного падения. Если принять маятник за математический, то его период Tм надо находить по формуле:
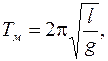 (2)
(2)
где l –длина маятника. Полагаем согласно условию длину l равной расстоянию от точки подвеса до центра масс шара:
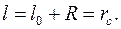 (3)
(3)
Таким образом, считая маятник математическим, мы заменяем шар материальной точкой, расположенной в его центре, что вызывает некоторую погрешность в вычислении периода.
С помощью формул (1) и (2) найдем отношение периодов Tф и Tм , учитывая соотношение (3):
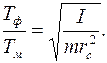 (4)
(4)
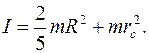 |
Момент инерции шара относительно оси, проходящей через точку подвеса, рассчитывается по теореме Штейнера:
Подставив это значение в (4), получим:
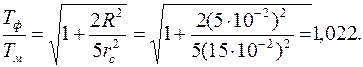 |
Отсюда найдем относительную погрешность в вычислении периода:
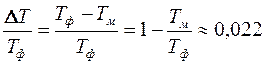 или 2,2%.
или 2,2%.
Задача 4.
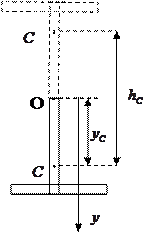 |
Маятник (в виде буквы Т) изготовлен из
двух стержней, имеющих одинаковую массу
и одинаковую длину 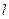 . Он может вращаться
. Он может вращаться
без трения вокруг горизонтальной оси,
проходящей через конец одного из стержней
(точка О). Какую минимальную угловую
скорость нужно сообщить маятнику в положении
равновесия, чтобы он совершил полный оборот?
Толщиной стержней пренебречь.
Решение
Будем считать, что в положении равновесия потенциальная энергия маятника равна нулю. Тогда, с учетом того, что в верхнем положении маятника его кинетическая энергия должна быть минимальна и, следовательно, равна нулю, закон сохранения энергии примет вид:
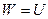 , (1)
, (1)
где 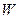 - кинетическая энергия, сообщенная маятнику в положении равновесия, а
- кинетическая энергия, сообщенная маятнику в положении равновесия, а 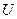 - его потенциальная энергия в верхнем положении. Потенциальная энергия тела рассчитывается по формуле
- его потенциальная энергия в верхнем положении. Потенциальная энергия тела рассчитывается по формуле
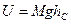 , (2)
, (2)
где 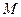 - масса тела, а
- масса тела, а 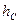 - высота его центра масс относительно нулевого уровня. В данном случае, за нулевой принят уровень, на котором находится центр масс маятника в положении равновесия
- высота его центра масс относительно нулевого уровня. В данном случае, за нулевой принят уровень, на котором находится центр масс маятника в положении равновесия
(точка С). В результате (см. рис.),
 . (3)
. (3)
Здесь, 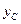 - координата центра масс маятника (ось
- координата центра масс маятника (ось 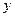 направлена вниз, а ее начало находится на той же высоте, что и ось вращения маятника). Применим формулу для нахождения координаты центра масс составного тела
направлена вниз, а ее начало находится на той же высоте, что и ось вращения маятника). Применим формулу для нахождения координаты центра масс составного тела
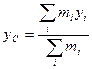 , (4)
, (4)
в которой 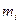 и
и 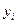 соответственно масса и координата центра масс iго тела. В нашем случае,
соответственно масса и координата центра масс iго тела. В нашем случае, 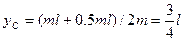 (
( 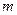 - масса одного стержня). Соответственно, из формулы (3),
- масса одного стержня). Соответственно, из формулы (3), 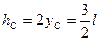 , а с учетом формулы (2), потенциальная энергия маятника
, а с учетом формулы (2), потенциальная энергия маятника
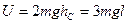 . (5)
. (5)
Теперь определим кинетическую энергию, сообщенную маятнику в положении равновесия. Кинетическая энергия тела, вращающегося вокруг неподвижной оси, равна
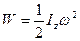 . (6)
. (6)
Здесь 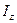 - момент инерции тела относительно оси вращения, а
- момент инерции тела относительно оси вращения, а 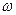 - его угловая скорость. Момент инерции маятника
- его угловая скорость. Момент инерции маятника 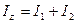 , где
, где 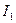 и
и 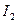 моменты инерции соответственно вертикального и горизонтального стержней относительно оси вращения. Известно, что момент инерции стержня относительно оси ,проходящей через его конец,
моменты инерции соответственно вертикального и горизонтального стержней относительно оси вращения. Известно, что момент инерции стержня относительно оси ,проходящей через его конец, 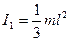 . Момент инерции горизонтального стержня найдем с помощью теоремы Штейнера:
. Момент инерции горизонтального стержня найдем с помощью теоремы Штейнера: 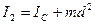 . В нашем случае,
. В нашем случае, 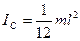 , а
, а 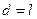 . Следовательно,
. Следовательно, 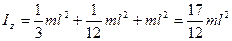 .
.
Подставив данное выражение для момента инерции в (6), получим
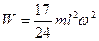 .
.  (7)
(7)
Подставив (5) и (7) в (1), получим
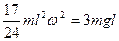 . Отсюда,
. Отсюда, 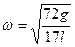 .
.
Задача 5.
Однородный сплошной цилиндр массой 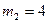 кг может вращаться без трения вокруг оси. За эту ось, нерастяжимой невесомой нитью, перекинутой через блок массой
кг может вращаться без трения вокруг оси. За эту ось, нерастяжимой невесомой нитью, перекинутой через блок массой 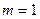 кг, он привязан к бруску массой
кг, он привязан к бруску массой 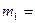 1 кг. Определить ускорение цилиндра вдоль наклонной плоскости и силу трения, действующую на него, при качении без проскальзывания. Блок вращается без трения. Угол наклона плоскостей к горизонту
1 кг. Определить ускорение цилиндра вдоль наклонной плоскости и силу трения, действующую на него, при качении без проскальзывания. Блок вращается без трения. Угол наклона плоскостей к горизонту 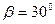 . Коэффициент трения бруска о плоскость
. Коэффициент трения бруска о плоскость 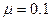 .
.
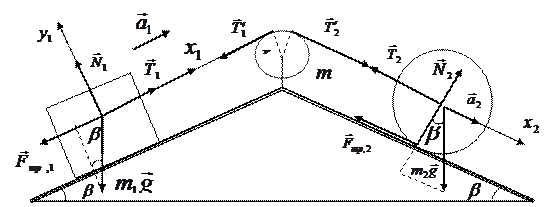 |
Решение:
На цилиндр действуют: сила тяжести 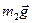 , сила натяжения нити
, сила натяжения нити 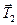 , сила реакции опоры
, сила реакции опоры 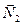 и сила трения
и сила трения 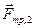 . Поскольку цилиндр катится без проскальзывания, то
. Поскольку цилиндр катится без проскальзывания, то 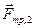 -- это сила трения покоя. Величина этой силы заранее неизвестна и находится в процессе решения (0
-- это сила трения покоя. Величина этой силы заранее неизвестна и находится в процессе решения (0 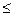
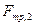
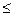
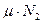 , где
, где 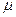 -- коэффициент трения). Силы, действующие на брусок, имеют тот же смысл и обозначены теми же буквами с индексом 1.
-- коэффициент трения). Силы, действующие на брусок, имеют тот же смысл и обозначены теми же буквами с индексом 1.
На блок действуют две силы натяжения  и
и 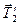 (
( 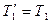 и
и 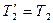 ). Между собой они неравны (
). Между собой они неравны (  ), так как в противном случае, результирующий вращающий момент, действующий на блок, равнялся бы нулю, и блок не вращался бы с ускорением.
), так как в противном случае, результирующий вращающий момент, действующий на блок, равнялся бы нулю, и блок не вращался бы с ускорением.
Чтобы решить задачу, для цилиндра запишем второй закон Ньютона и уравнение динамики вращательного движения, для блока -- уравнение динамики вращательного движения, а для бруска -- второй закон Ньютона. Кроме того, будем использовать следующую связь между линейным ускорением центра масс цилиндра 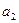 и его угловым ускорением
и его угловым ускорением 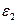 , которая справедлива при качении без проскальзывания:
, которая справедлива при качении без проскальзывания:
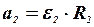 , (1)
, (1)
где 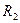 -- радиус цилиндра (в силу нерастяжимости нити, ускорения центров масс цилиндра и бруска одинаковы, то есть
-- радиус цилиндра (в силу нерастяжимости нити, ускорения центров масс цилиндра и бруска одинаковы, то есть  ). Если нить не проскальзывает относительно блока, то формула (1) также связывает его угловое ускорение
). Если нить не проскальзывает относительно блока, то формула (1) также связывает его угловое ускорение 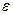 с линейным ускорением центров масс бруска и цилиндра
с линейным ускорением центров масс бруска и цилиндра  (В этом случае,
(В этом случае, 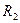 в ней нужно заменить на радиус блока
в ней нужно заменить на радиус блока 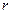 ).
).
Рассмотрим качение цилиндра. Второй закон Ньютона для него имеет
следующий вид:
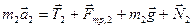 . (2)
. (2)
Спроектировав (2) на ось 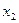 , получим с учетом условия
, получим с учетом условия 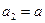 , что
, что
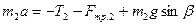 . (3)
. (3)
При записи уравнения динамики вращательного движения цилиндра относительно его оси симметрии, учтем, что моменты сил тяжести, реакции опоры и натяжения нити равны нулю (их плечи равны нулю). В результате, уравнение динамики вращательного движения примет следующий вид:
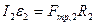 . (4)
. (4)
Здесь 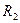 -- радиус цилиндра,
-- радиус цилиндра,
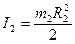 (5)
(5)
-- его момент инерции, а  -- момент силы трения относительно оси симметрии цилиндра. Подставим в (4) соотношения (5) и выражение для углового ускорения цилиндра
-- момент силы трения относительно оси симметрии цилиндра. Подставим в (4) соотношения (5) и выражение для углового ускорения цилиндра 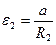 , которое следует из (1):
, которое следует из (1):
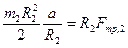 .
.
В результате, после сокращения на 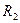 , получим:
, получим:
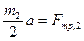 . (6)
. (6)
Если рассматривать качение изолированного цилиндра, то уравнений (3) и (6) достаточно для решения задачи, так как тогда, из-за отсутствия нити, 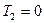 , а два уравнения позволяют определить две неизвестные величины
, а два уравнения позволяют определить две неизвестные величины  и
и 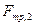 . В данном случае, сила
. В данном случае, сила  неизвестна, и приходится рассматривать скольжение бруска и вращение блока.
неизвестна, и приходится рассматривать скольжение бруска и вращение блока.
Рассмотрим скольжение бруска. Запишем второй закон Ньютона в векторном виде
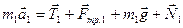 , (7)
, (7)
а затем, спроектируем его на ось 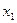 :
:
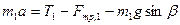 . (8)
. (8)
Здесь, 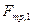 -- сила трения скольжения. Поэтому ее можно рассчитать по формуле
-- сила трения скольжения. Поэтому ее можно рассчитать по формуле 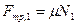 . Для нахождения
. Для нахождения 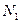 , спроектируем (7) на ось
, спроектируем (7) на ось 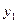 :
:
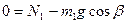 .
.
Отсюда, 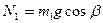 и
и 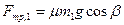 . Подставив данное выражение для силы трения в (8), получим
. Подставив данное выражение для силы трения в (8), получим
 . (9)
. (9)
Если бы масса блока равнялась нулю, то сила натяжения была бы одинаковой в пределах всей нити ( 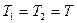 ). Тогда, трех уравнений (3), (6), (9) было бы достаточно для нахождения трех неизвестных
). Тогда, трех уравнений (3), (6), (9) было бы достаточно для нахождения трех неизвестных 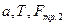 . В данном случае, неизвестных четыре (
. В данном случае, неизвестных четыре ( 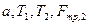 ), и приходится использовать еще уравнение динамики вращательного движения блока:
), и приходится использовать еще уравнение динамики вращательного движения блока:
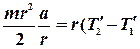 ).
).
Здесь момент силы натяжения 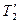 ускоряющий и, поэтому, положительный (
ускоряющий и, поэтому, положительный ( 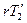 ), момент силы
), момент силы 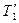 -- тормозящий и, поэтому, отрицательный (
-- тормозящий и, поэтому, отрицательный ( 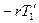 ), а угловое ускорение блока
), а угловое ускорение блока 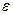 выражено через
выражено через  с помощью формулы (1).
с помощью формулы (1).
В результате, сократив на 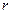 и заменив
и заменив 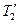 и
и  на
на 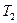 и
и 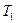 , получим:
, получим:
 . (10)
. (10)
Теперь все сводится к решению системы уравнений (3), (6), (9), (10). Сложим эти уравнения почленно:
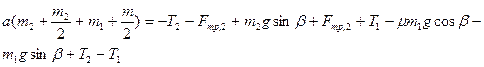
Приведя подобные члены и проведя сокращение, получим:
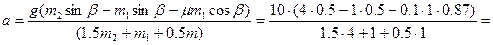 1.88 м/с2
1.88 м/с2
Сила трения 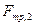 находится из уравнения (6):
находится из уравнения (6): 
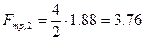 Н .
Н .
В заключение напомним, что, если масса блока равна нулю, то сила натяжения одинакова на всем протяжении нити, и, поэтому, нет необходимости использовать уравнение динамики вращательного движения блока.
Кроме того, отметим, что поступательно движущаяся система отсчета, связанная с осью цилиндра, является неинерциальной, так как цилиндр катится с ускорением. Поэтому уравнение динамики вращательного движения цилиндра относительно его оси симметрии должно содержать момент силы инерции. Однако этот момент равен нулю, так как сила инерции приложена в центре масс цилиндра и, следовательно, имеет нулевое плечо.
адача 6.
Тело массой m, находящееся на вершине наклонной плоскости, удерживается силой трения. За какое время тело спустится с наклонной плоскости, если она станет двигаться в горизонтальном направлении с ускорением а0= 1,00 м/с2. Длина плоскости l = 1,0 м, угол наклона к горизонту a=30°, коэффициент трения между телом и плоскостью m = 0,60.
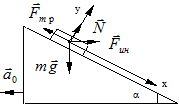
Решение. Выберем систему отсчета, связанную с наклонной плоскостью. Пока плоскость покоится, на тело действуют три силы: сила тяжести 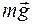 , сила нормального давления
, сила нормального давления 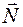 опоры и сила трения покоя
опоры и сила трения покоя 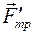 , которые уравновешивают друг друга. Как только начнется ускоренное движение плоскости и связанная с ней система отсчета станет неинерциальной, появится четвертая сила, действующая на тело,–сила инерции
, которые уравновешивают друг друга. Как только начнется ускоренное движение плоскости и связанная с ней система отсчета станет неинерциальной, появится четвертая сила, действующая на тело,–сила инерции 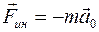 . Равновесие нарушится и тело начнет скользить вниз по наклонной плоскости с ускорением
. Равновесие нарушится и тело начнет скользить вниз по наклонной плоскости с ускорением 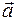 . Так как искомое время определяется известной формулой, связывающей время и перемещение, при равноускоренном движении без начальной скорости:
. Так как искомое время определяется известной формулой, связывающей время и перемещение, при равноускоренном движении без начальной скорости:
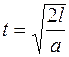 , (1)
, (1)
то надо найти ускорение a. Для этого запишем второй закон Ньютона в нашей неинерциальной системе отсчета:
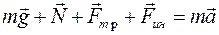 (2)
(2)
Направим оси координат, как показано на рисунке. Проектируя все векторы, входящие в уравнение (2), на оси x и y, получим соответственно два скалярных уравнения:
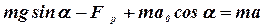 (3)
(3)
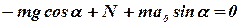 (4)
(4)
Решив систему (3), (4) с учетом 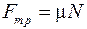 , найдем ускорение:
, найдем ускорение:
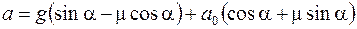 .
.
Теперь по формуле (1) имеем
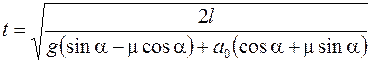 .
.
Подставив числовые значения величин, найдем

 .
.
Задача 7.
Собственное время жизни нестабильной элементарной частицы мюона равно 2.2мкс. Определить время жизни мюона в системе отсчета, где до распада он успевает пройти 20 км.
Решение.
Для решения этой задачи проще всего воспользоваться инвариантностью интервала между событиями .
В системе отсчета К, где мюон покоится, интервал ΔS между его рождением и распадом равен  , где Dt –собственное время жизни частицы.
, где Dt –собственное время жизни частицы.
В системе отсчета К¢, где мюон успевает пройти до распада 20км, интервал ΔS΄ между его рождением и распадом равен  , где Dl¢ расстояние, разделяющее точки рождения и распада мюона в системе отсчета К¢.
, где Dl¢ расстояние, разделяющее точки рождения и распада мюона в системе отсчета К¢.
Интервал между этими событиями остается постоянным при переходе от одной инерциальной системе к другой.
Следовательно:  =
=  .
.
Решая это уравнение получим: Dt¢= 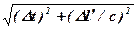 =
= 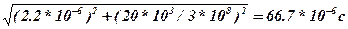 .
.
Следует отметить что полученный результат превосходит собственное время жизни в 30 раз!
Задача 8.
В дне цилиндрического сосуда имеется круглое отверстие диаметром 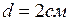 . Диаметр сосуда
. Диаметр сосуда  . Найти зависимость скорости
. Найти зависимость скорости 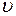 понижения уровня воды в сосуде от высоты
понижения уровня воды в сосуде от высоты 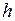 этого уровня. Определить численное значение этой скорости для высоты
этого уровня. Определить численное значение этой скорости для высоты 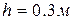 .
.
Решение.
Рассмотрим состояние жидкости в верхнем сечении сосуда и в сечении отверстия. По формуле Бернулли:
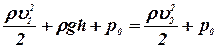 или
или 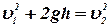 , (1)
, (1)
где 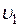 - скорость течения воды в верхнем сечении (скорость понижения уровня воды в сосуде),
- скорость течения воды в верхнем сечении (скорость понижения уровня воды в сосуде), 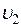 - скорость вытекания воды из отверстия, p0-атмосферное давление, h-высота верхнего уровня жидкости относительно отверстия. Вследствие несжимаемости жидкости:
- скорость вытекания воды из отверстия, p0-атмосферное давление, h-высота верхнего уровня жидкости относительно отверстия. Вследствие несжимаемости жидкости:  или
или 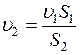 , (2)
, (2)
где 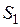 - площадь поперечного сечения сосуда,
- площадь поперечного сечения сосуда, 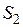 - площадь поперечного сечения отверстия.
- площадь поперечного сечения отверстия.
Подставляя (2) в (1) и решая относительно 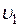 ,получим :
,получим :
 .
.
Так как 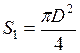 и
и 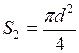 , то
, то 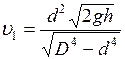 .
.
Так как 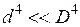 , то приближённо
, то приближённо
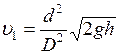 . (3)
. (3)
Подставив числовые значения в формулу (3), найдём:
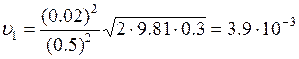 м/с.
м/с.
Задача 9.
Платформа, имеющая форму сплошного однородного диска, может свободно вращаться вокруг вертикальной оси. На краю платформы находится человек, масса которого в 4 раза меньше массы платформы. Найти отношение угловых скоростей вращения платформы в начальный момент и после того, как человек переместится в её центр. Человека рассматривать как материальную точку.
Решение.
Внешними силами в системе человек-платформа являются силы тяжести, направленные вертикально вниз. Проекция момента внешних сил на вертикальную ось, совпадающую с осью вращения платформы, равна нулю. Следовательно, момент импульса системы человек-платформа относительно оси вращения должен оставаться неизменным при перемещении человека относительно платформы:
I сист ω = I΄сист ω΄,
где: I сист - момент инерции системы до изменения положения человека, I΄сист - момент инерции системы после изменения положения человека, ω и ω΄ - угловые скорости системы соответственно до и после изменения положения человека. Момент инерции системы равен сумме моментов инерции тел, входящих в состав системы, следовательно, I сист = I1 + I2 , где I1 – момент инерции платформы, I2 – момент инерции человека.
Таким образом, I сист = 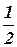 m1 R2 +m2 R2, где : m1 и m2 –массы платформы и человека, R – радиус платформы.
m1 R2 +m2 R2, где : m1 и m2 –массы платформы и человека, R – радиус платформы.
После того, как человек переместится в центр платформы, момент инерции платформы относительно оси вращения не изменится, а момент инерции человека обратится в нуль. С учетом этого получаем:
I΄сист = 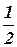 m1 R2.
m1 R2.
Таким образом, закон сохранения момента импульса системы можно представить в виде:
( 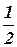 m1 R2 +m2 R2) ω =
m1 R2 +m2 R2) ω = 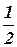 m1 R2 ω΄.
m1 R2 ω΄.
Найдем отношение угловых скоростей системы до и после перемещения:
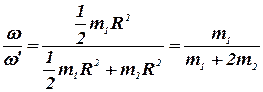 ,
,
С учетом того, что m1 =4 m2, окончательно получим:
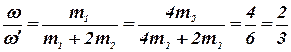 .
.
