Эллипстің параметрлік теңдеуі.
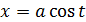
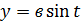
27. Гипербола (канондық теңдеуін қорыту, фокалдық радиустар, эксцентриситет, параметрлік теңдеу, асимптоталар). F1,F2 нүктелеріне дейінгі арақашықтықтарының айырмасының модулы тұрақты сан болатын жазықтықтағы нүктелер жиынын гипербола деп атаймыз.
|r1-r2|=2a
Фокалдық радиустар:
r1= 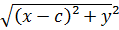 , r2=
, r2= 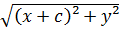
Канондық теңдеуін қорыту:
| 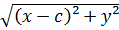 –
– 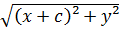 |=2a
|=2a
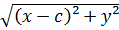 =
= 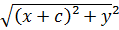 ±2a
±2a
x2-2cx+c2+y2=x2+2cx+c2+y2±4a 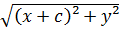 +4a2
+4a2
cx+a2=±a 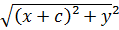
c2x2+2a2cx+a4=a2x2+2a2cx+a2c2+a2y2
x2(c2-a2)-a2y2=a2(c2-a2)
c2-a2=b2
x2b2-a2y2=a2b2
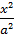 -
- 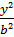 = 1
= 1
Гиперболаның экцентриситеті деп, келесі санды айтамыз:
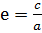 c>a, e>1
c>a, e>1
Гиперболалық косинус пен гиперболалық синус:
cht= 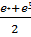
sht = 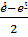
Параметрлік теңдеу:
cht =  , sht=
, sht= 
Асимптота дегеніміз гипербола шексіз жуықтайтын түзу.
y =  x; y= -
x; y= -  x.
x.
28. Парабола. Бізге жазықтықта (.) F нүктесі және  түзуі берілсін,
түзуі берілсін, 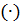 F
F 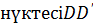 түзуіне тиісті емес.
түзуіне тиісті емес.
Анықтама.Жазықтықтағы нүктелер жиынын парабола деп атайды, егер сол жиынның әр бір нүктесінің 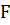 нүктесіне дейінгі арақашықтығы және
нүктесіне дейінгі арақашықтығы және 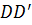 түзуіне дейінгі арақашықтықтары тең болса.
түзуіне дейінгі арақашықтықтары тең болса.
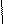






 y M
y M
d r 




D( 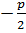 ,,0)
,,0) 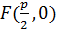
 x
x
Бұл жерде F – фокус, 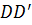 директриса, фокуспен директрисаның арасындағы арақашықты параболаның параметрі
директриса, фокуспен директрисаның арасындағы арақашықты параболаның параметрі 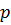 деп атайды.
деп атайды.
Параболаның 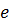 – сін бірге тең деп аламыз,
– сін бірге тең деп аламыз, 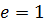 .
.
Бізде 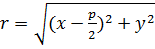 ,
, 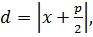 егер
егер 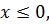 онда минус таңбасы шығады
онда минус таңбасы шығады
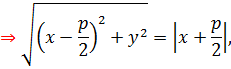
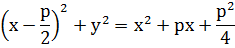
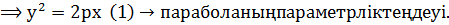
Сондықтан, 1) егер (.) 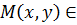 парабола
парабола 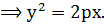
2) егер (.) 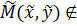 парабола
парабола 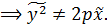
29. Матрицаларды санға көбейту амалы және оның қасиеттері. (дәлелдеумен)
Матрицаны санға көбейту үшін оның барлық элементтерін сол санға көбейтеміз.
Кез келген γ Є IR, A берілсін. A= { aij }
γА= { γaij }
Қасиеттері:
1) 1·A=A
2) (γ·μ)·A= γ·(μ·A)=μ·(γ·A)
3) γ·(A+B)=γ·A+γ·B
4) (γ+μ)·A=γ·A+μ·B
30. Матрицаларды қосу амалы және оның қасиеттері (дәлелдеуімен). Матрица дегеніміз сандардан тұратын таблица. Матрицалар квадрат, үшбұрышты т.с.с. болады. Матрицаларды қосу оның элементтері (сәйкес) бойынша жүргізіледі. Транспонирленген матрица. А= 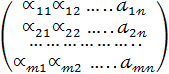
αίJ– сандары матрицаның элементтері. i –жол, j –баған. Қысқаша А=(αίJ). ЕгербарлықαίJ = 0 болса, онда матрица нөлдік матрица. Егерекі Ажәне В матр-ныңсәйкесорындардатұратынэлементтерітеңболса, онда А=В. Егержол мен бағанныңгержол мен бағанныңорындарынауыстырсақ, ондатранспонирленген матрица аламыз. Реттерібірдейматрицалардықосуғаболады. Айталық, А=( αίJ), В=( bίJ) болсын, сонда А+В = (αίJ + bίJ). Матрицалардықосудыңқасиеттері:
1. А+В = В+А;2. А+0 = А;3. А+(В+С) = (А+В)+С. Егер А матрицасыныңбарлықэлементтерінµсанынакөбейтсек, ондаµ А = (µαίJ). Матр-нысанғакөбейтудіңқасиеттері: 1)1*А=А*1=А ;2) µ (ℓ А) = (µ ℓ )А ; 3)µ (А+В) =µА+ µВ; 4) (µ+ℓ)А = µ А +ℓ А;
Дәләлдеуі: А = 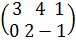
В = 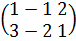 А+В =
А+В = 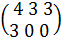 .
.
31. Матрицаны аудару амалы және оның қасиеттері. Матрицаның жолдарымен бағандарының орындарын ауыстыруды оны транспонирлеу деп аталады. А матрицасына осы амалды қолданғанда шыққан матрицаны А' арқылыбелгілейміз. А= 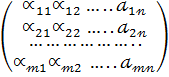
А'= 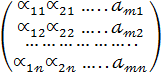
A/ - n*m; A – m*n;
Аудару амалының қасиеттері:1)(A/)/ =A ; 2) (λA)/ = λ* A/ ;
3) (A+B)/ = A/+B/; 4) (A*B)/ = B/*A/. Дәлелдеуі: А = 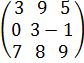 А'=
А'= 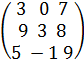
32. Матрицаларды көбейтуA-m*k ретті, B-k*n ретті.
Cij=αi1+b1j+ αi2+b2j+….+ (i=1,2……..m) (j=1,2……...n)
формулаларымен анықталатын C=A·B матрицасы А мен В матрицасының көбейтіндісі деп аталады.С матрицасы ретті m* n болады.
Матрицаға қолданылатын амалдар қасиеттері:
1)A+B=A+B;
2) (A+B)+C=A+(B+C); 3)λ*(A+B)= λ*A+ λ*B ; 4) A*(B+C)=A*B+A*C;
5) (A+B)*C=AC+BC ;
6) λ(A*B)=(λ*A)*B=А*( λ*B); 7) A*(B*C)=(A*B)*C. Дәләлдеуі: A = 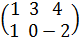 2 х 3 ретті, B =
2 х 3 ретті, B = 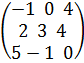 3 х 3 ретті
3 х 3 ретті
A*B = 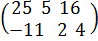 .
.
