Изучение оптических систем
Лабораторная работа № 4. 2
Цель работы: изучение линз и систем линз и определение их фокусного расстояния (оптической силы).
I. Основные понятия и определения
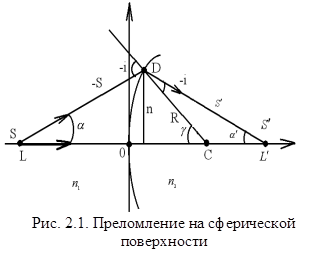 Рассмотрим отражение, и преломление света на сферической границе раздела прозрачных сред с показателями преломления n1 и n2. будем рассматривать только те лучи, для которых угол
Рассмотрим отражение, и преломление света на сферической границе раздела прозрачных сред с показателями преломления n1 и n2. будем рассматривать только те лучи, для которых угол 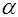 мал (см. рис.2.1). Такие лучи называются параксиальными. При этом правило знаков:
мал (см. рис.2.1). Такие лучи называются параксиальными. При этом правило знаков:
1) все расстояния от поверхности (точка О) влево–отрицательны; вправо–положительны;
2) вверх от точки О – положительны, вниз – отрицательны;
3) углы, отсчитываемые от прямой LL' – положительны, если их тангенсы и синусы положительны и отрицательны, если их тангенсы и синусы отрицательны.
С учётом малости углов закон преломления в точке D можно записать:
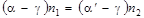
Имея ввиду, что 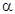 =h/s,
=h/s, 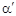 = h/s',
= h/s', 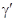 =h/R, получим:
=h/R, получим:
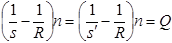 (2.1)
(2.1)
Здесь: Q – инвариант Аббе, величина D= 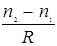 – поверхности.
– поверхности.
Если источник S удалить в бесконечность, то лучи пересекутся в точке заднего фокуса 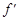 . Если источник S находится от зеркала на расстоянии –s =
. Если источник S находится от зеркала на расстоянии –s = 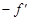 , то во второй среде лучи будут параллельны. Эта точка – передней фокус поверхности. Тогда
, то во второй среде лучи будут параллельны. Эта точка – передней фокус поверхности. Тогда
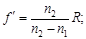
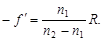
Отсюда: 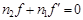 .
.
Из формулы (2.1) также следует, что 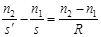 или
или 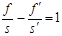 . (2.2)
. (2.2)
Если заменить п1, на – п2, то получим формулу сферического зеркала
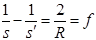
Здесь 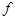 – фокусное расстояние зеркала. Следует отметить, что все выражения не зависят от угла, что является следствием параксиальности лучей. Поэтому под s и
– фокусное расстояние зеркала. Следует отметить, что все выражения не зависят от угла, что является следствием параксиальности лучей. Поэтому под s и 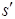 следует понимать, кратчайшие расстояния LO и
следует понимать, кратчайшие расстояния LO и 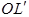 .
.
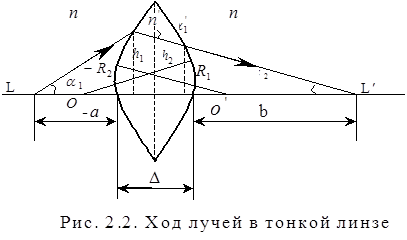 Рассмотрим прохождение света через две сферические поверхности, расположенные так, как показано на рис. 2.2. Прозрачное тело с показателем преломления окружающей среды, ограниченное сферическими или цилиндрическими поверхностями называется линзой.
Рассмотрим прохождение света через две сферические поверхности, расположенные так, как показано на рис. 2.2. Прозрачное тело с показателем преломления окружающей среды, ограниченное сферическими или цилиндрическими поверхностями называется линзой.
Для некоторого параксиального луча можно записать:
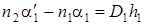 ,
,
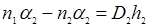 ,
,
сложив уравнения, получим 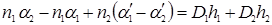 , где
, где 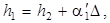
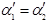 . Если положить Δ малым (тонкая линза), то получим формулу тонкой линзы:
. Если положить Δ малым (тонкая линза), то получим формулу тонкой линзы:
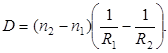 (2.3)
(2.3)
Поделив на h, получим формулу оптической системы:
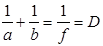 , т.к.
, т.к. 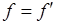 . (2.4)
. (2.4)
Следует отметить, что для зеркала расстояния a и b отсчитываются от полюса (т.О на рис.2.1) зеркала. Введём формулу линейного и углового увеличения сферической поверхности.
Линейным увеличением 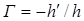 называется отношение поперечных размеров изображения и предмета. Угловым увеличением
называется отношение поперечных размеров изображения и предмета. Угловым увеличением 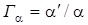 называется отношение углов схода и выхода параксиальных лучей. Линейное и угловое увеличение связаны соотношением
называется отношение углов схода и выхода параксиальных лучей. Линейное и угловое увеличение связаны соотношением 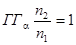 .
.
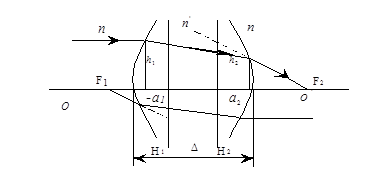 Сопряжённые плоскости, для которых Г=1 называются главными. Для одной поверхности и тонкой линзы они сливаются в одну, Н, которая для тонкой линзы проходит через оптический центр линзы, т.е. точку в которой пересекаются оптические оси линзы. Оптическая ось – направление, в котором лучи идут без преломления. Оптическая ось, перпендикулярная главной плоскости, называется главной. На ней лежат главные фокусы и оптический центр. Остальные оптические оси и фокусы называются побочными.
Сопряжённые плоскости, для которых Г=1 называются главными. Для одной поверхности и тонкой линзы они сливаются в одну, Н, которая для тонкой линзы проходит через оптический центр линзы, т.е. точку в которой пересекаются оптические оси линзы. Оптическая ось – направление, в котором лучи идут без преломления. Оптическая ось, перпендикулярная главной плоскости, называется главной. На ней лежат главные фокусы и оптический центр. Остальные оптические оси и фокусы называются побочными.
Множество фокусов образуют фокальные плоскости, проходящие через главные фокусы и параллельные главным плоскостям. Если линза толстая, то её оптическая сила
Рис. 2.3. Ход лучей в толстой линзе
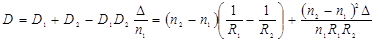 . (2.5)
. (2.5)
Ход лучей в толстой линзе показан на рис. 2.3.
Рассмотрим геометрию и построение изображений в тонкой линзе.
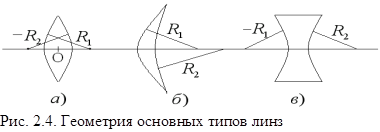 Для линз а) и б) оптическая сила положительная, для в) – отрицательная. Соответственно в формулах (2.3) и (2.4) следует учитывать знаки для а, b, f, R1, R2. рис.2.4.
Для линз а) и б) оптическая сила положительная, для в) – отрицательная. Соответственно в формулах (2.3) и (2.4) следует учитывать знаки для а, b, f, R1, R2. рис.2.4.
Для построения изображений в линзах используются три луча (рис.2.5).
Изоражения 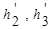 – действительное,
– действительное, 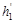 -мнимое. Все изображения мнимые.
-мнимое. Все изображения мнимые.
Для системы тонких линз оптическая сила D = 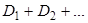 , при этом система линз тонкая.
, при этом система линз тонкая.
II. Методика эксперимента
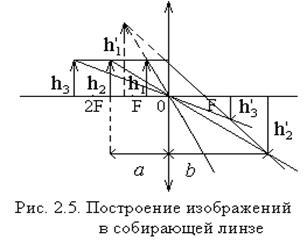 |
Из выражения (2.4) и рис.2.5, следует, что предмет и изображение можно поменять местами, не изменяя общего расстояния L=a+b между изображением и предметом. Это свойство линз положено в основу работы. Как следует из рис.2.5:
a-b= 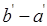 =l;
=l; 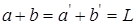 (2.6)
(2.6)
Подставим a и b из (2.6) в формулу оптической системы (2.4), получим:
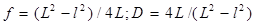 . (2.7)
. (2.7)
III. Проведение эксперимента и обработка результатов
1. Включить осветитель в качестве предмета используется светящаяся буква осветителя. Выбрать и установить на скамью линзу.
2. Получить увеличенное и уменьшенное изображения буквы, меняя положения экрана и осветителя. Определить L и l .Определить f и D. Результаты занести в таблицу.
3. Выполнить измерение по пункту 2.2 ещё для двух значений L.
4. Выполнить измерение по пункту 2.3 ещё для одной линзы.
5. Составив из двух линз систему, провести измерение по пункту 2.3 для неё.
6. Проверить результат измерений для системы линз по формулам тонкой и толстой линз.
