Информация об экзаменационной работе

Общее время экзамена – 235 минут.

Характеристика работы. Всего в работе 22 задания, из которых 16 заданий базового уровня (часть 1), 4 задания повышенного уровня (часть 2) и 2 задания высокого уровня сложности (часть 2). Работа состоит из четырёх модулей: «Алгебра», «Геометрия», «Вероятность и статистика», «Реальная математика».

Модуль «Алгебра» содержит 10 заданий: в части 1 — семь заданий;
в части 2 — три задания. Модуль «Геометрия» содержит пять заданий:
в части 1 — три задания; в части 2 — два задания. Модуль «Вероятность и статистика» содержит три задания: в части 1 — два задания; в части 2 — одно задание .Модуль «Реальная математика» содержит четыре заданий: все задания этого модуля — в части 1.

Советы и указания по выполнению работы. Сначала выполняйте задания части 1. Начать советуем с того модуля, задания которого вызывают у Вас меньше затруднений, затем переходите к другим модулям. Для экономии времени пропускайте задание, которое не удаётся выполнить сразу, и переходите к следующему. Если у Вас останется время, Вы сможете вернуться к пропущенным заданиям.

Все необходимые вычисления, преобразования и т.д. выполняйте
в черновике. Записи в черновике не учитываются при оценивании работы. Если задание содержит рисунок, то на нём непосредственно в тексте работы можно выполнять необходимые Вам построения. Рекомендуем внимательно читать условие и проводить проверку полученного ответа.

Ответы к заданиям 2 и 13 записываются в виде одной цифры, которая соответствует номеру правильного ответа. Эту цифру запишите в поле ответа в тексте работы.

Для остальных заданий части 1 ответом является число или последовательность цифр, которые нужно записать в поле ответа в тексте работы. Если в ответе получена обыкновенная дробь, обратите её в десятичную. В случае записи неверного ответа на задания части 1 зачеркните его и запишите рядом новый.

Решения заданий части 2 и ответы к ним запишите на отдельном листе или бланке. Задания можно выполнять в любом порядке, начиная с любого модуля. Текст задания переписывать не надо, необходимо только указать его номер.

При выполнении работы Вы можете воспользоваться справочными материалами.

Оценивание работы. Баллы, полученные за верно выполненные задания, суммируются. Для успешного прохождения итоговой аттестации необходимо набрать в сумме не менее 8 баллов. За каждое правильно выполненное задание части 1 выставляется 1 балл. Каждое правильно выполненное задание части 2 оценивается в 2 балла.

Желаем успеха!

Часть 1

Модуль «Алгебра»

1

Найдите значение выражения .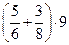

Ответ: ___________________________.

2

На координатной прямой отмечено число .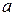

Какое утверждение относительно этого числа является верным?

1)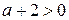

2)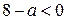

3)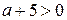

4)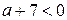

Ответ:

3

Найдите значение выражения .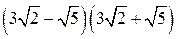

Ответ: ___________________________.

4

Решите уравнение .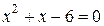

Ответ: ___________________________.

5

Установите соответствие между графиками функций и формулами, которые их задают.

ГРАФИКИ

А)		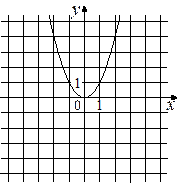Б)		В)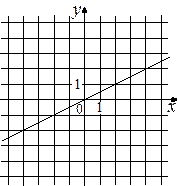

ФОРМУЛЫ

1)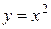

2)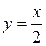

3)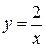

В таблице под каждой буквой, соответствующей графику, впишите номер формулы, которая его задаёт.

Ответ:	А	Б	В

6

Дана геометрическая прогрессия: 1, 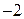, 4, … Найдите сумму первых её 7 членов.

Ответ: ___________________________.

7

Найдите значение выражения 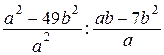при , .

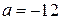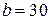Ответ: ___________________________.

Модуль «Геометрия»

8

В треугольнике 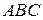известны стороны: 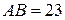, , 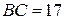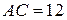. Точка 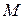— середина 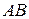, а точка 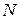— середина 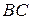. Найдите длину отрезка .

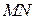Ответ: ___________________________.

9

В треугольнике 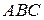угол равен 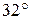, угол 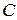равен 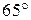, 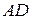— биссектриса, 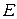— такая точка на 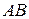, что 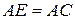. Найдите угол 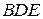. Ответ дайте в градусах.

Ответ: ___________________________.

10

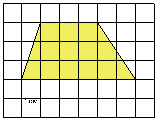Найдите площадь трапеции, изображённой на рисунке.

Ответ: ___________________________.

Модуль «Вероятность и статистика»

На диаграмме показана среднемесячная температура воздуха в Санкт-Петербурге за каждый месяц 1999 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме разность между наибольшей и наименьшей среднемесячными температурами в 1999 году. Ответ дайте в градусах Цельсия.

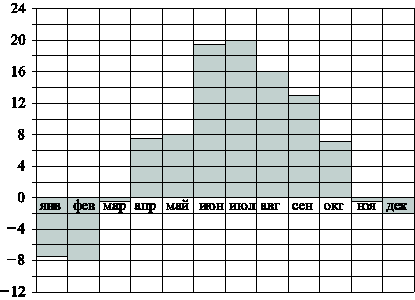
Ответ: ___________________________.

На тарелке 30 пирожков: 4 с мясом, 14 с капустой и 12 с вишней. Катя наугад берёт один из пирожков. Найдите вероятность того, что он окажется с вишней.

12

11

Модуль «Реальная математика»

13

В таблице приведены нормативы по бегу на 30 метров для учащихся 9-х классов.

	Мальчики	Девочки
Отметка	«отл.»	«хор.»	«удовл.»	«отл.»	«хор.»	«удовл.»
Время, секунды	4,6	4,9	5,3	5,0	5,5	5,9

Какую отметку получит девочка, пробежавшая эту дистанцию за 5,36 секунды?

1)	отлично	2)	хорошо
3)	удовлетворительно	4)	норматив не выполнен

Ответ:

16

14

Товар на распродаже уценили на 25%, при этом он стал стоить 900 рублей. Сколько рублей стоил товар до распродажи?

Ответ: ___________________________.

15

Период колебания математического маятника 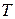(в секундах) приближенно можно вычислить по формул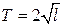е , где 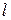— длина нити (в метрах). Пользуясь этой формулой, найдите длину нити маятника (в метрах), период колебаний которого составляет 3 секунды.

Ответ: ___________________________.

Некоторые из сотрудников фирмы отдыхали в Крыму, а те, кто не отдыхал в Крыму, отдыхали в Сочи. При этом среди сотрудников этой фирмы есть те, кто не отдыхал в Крыму. Какие из следующих утверждений верны.

1) Найдётся сотрудник фирмы, который не отдыхал летом ни в Крыму, ни в Сочи.

2) Если Мария Алексеевна не отдыхала летом ни в Крыму, ни в Сочи, то она не является сотрудником этой фирмы.

3) Среди сотрудников фирмы найдётся отдыхавший в Сочи, но не в Крыму.

4) Каждый из сотрудников фирмы отдыхал или в Крыму, или в Сочи.

Ответ: ___________________________.

Часть 2

При выполнении заданий 17–22 используйте отдельный лист. Сначала укажите номер задания, а затем запишите его решение и ответ. Пишите чётко и разборчиво.

17

Решите систему неравенств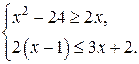

18

Расстояние между городами А и В равно 140 км. Из города А в город В выехал автомобиль, а через 20 минут следом за ним со скоростью 75 км/ч выехал мотоциклист. Мотоциклист догнал автомобиль в городе С и повернул обратно. Когда он проехал половину пути из С в А, автомобиль прибыл в В. Найдите расстояние от А до С.

19

Постройте график функции и определите, при каких значениях 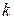прямая 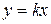имеет с графиком ровно одну общую точку.

20

Окружность, проходящая через вершины 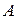и 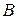треугольника 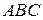, пересекает стороны 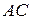и 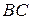в точках 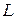и 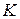соответственно, отличных от 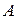и 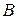. Докажите, что треугольник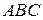и и 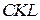подобны.

21

Углы при одном из оснований трапеции равны 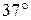и 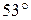, а отрезки, соединяющие середины противоположных сторон, равны 21 и 12. Найдите основания трапеции.

22

Спортсмен стреляет по пяти мишеням. Вероятность попадания в мишень при одном выстреле равна 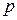. На каждую мишень спортсмен имеет две попытки.

а) Найдите вероятность того, что спортсмен попадёт в первую мишень.

б) Найдите вероятность того, что спортсмен попадёт ровно в четыре мишени.