В этой теме рассматриваются два вопроса: 1) напряжения в движущихся деталях; 2) напряжения при ударе. В первом случае динамическое воздействие сводится к дополнительной статической нагрузке соответствующими силами инерции. Во втором – учесть силы инерции невозможно, так как неизвестна продолжительность удара. Напряжения при ударе вычисляют, приравняв кинетическую энергию ударяющего тела потенциальной энергии деформации стержня, воспринимающего удар. Весьма существенно, что напряжения при продольном ударе зависят не только от площади поперечного сечения стержня, но и от его длины и модуля упругости материала.
После изучения этой темы можно решать задачу 14, включённую в контрольные работы.
Литература:[4, гл. 15]; [5, гл. 14]; [6, гл. 14, задачи: 1, 2, 7, 42, 47, 54, 59, 62, 64]; [7, гл. 17].
Вопросы для самопроверки
119. Как вычисляют напряжения в деталях при равноускоренном поступательном движении?
120. Что называется динамическим коэффициентом?
121. От каких факторов зависят напряжения в ободе вращающегося колеса?
122. Как находят напряжения в спарниках и шатунах?
123. Как находят напряжения во вращающемся диске постоянной толщины?
124. Как выводят формулу для определения напряжений при ударе?
125. Чему равен динамический коэффициент при ударе?
126. Как изменится напряжение при продольном ударе в случае увеличения площади поперечного сечения в два раза? (При ответе можно пользоваться приближенной формулой).
127. Зависит ли напряжение при изгибающем ударе от материала балки?
128. В каком случае при изгибающем ударе напряжения больше: при положении на ребро или плашмя?
129. Каким путём можно уменьшить напряжение в стержне с выточками при продольном ударе?
130. Как учитывается масса упругой системы, испытывающей удар?
131. Как производят испытания на удар?
Тема 12.РасчЁт на прочность при напряжениях,
Циклически изменяющихся во времени
Расчёт на прочность при напряжениях, циклически изменяющихся во времени, имеет важное значение, так как в деталях машин часто возникают переменные напряжения. Надо хорошо уяснить понятие предела выносливости и научиться строить диаграммы для несимметричного цикла. Необходимо также знать все факторы, от которых зависит коэффициент концентрации напряжений. Особое внимание обратите на практические меры по борьбе с изломами усталости: а) повышение предела прочности при достаточной пластичности; б) создание однородной мелкозернистой структуры; в) проектирование внешних очертаний детали без резких переходов; г) тщательная обработка поверхности.
Надо подробно разобрать примеры определения допускаемых напряжений для различных деталей машин, воспринимающих переменные нагрузки. Правильный выбор допускаемого напряжения и формы сечения обеспечивает более экономное использование материала.
Литература:[5, гл. 15]; [6, гл. 14, задачи: 72, 78, 85] ]; [7, гл. 19].
Вопросы для самопроверки
132. Что называется пределом выносливости?
133. Какова эмпирическая зависимость между пределом выносливости и пределом прочности?
134. Как находят предел выносливости при несимметричном цикле?
135. Какие напряжения называются местными?
136. В чём разница между теоретическим и действительным коэффициентами концентрации напряжений?
137. Как влияет характер обработки материала на действительный коэффициент концентрации напряжений?
138. Как влияют размеры детали на предел выносливости?
139. Как устанавливают допускаемые напряжения при переменных напряжениях?
140. Какие практические меры применяют по борьбе с изломами усталости?
КОНТРОЛЬНЫЕ РАБОТЫ
Задача 1
РАСЧЁТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМОЙ СТЕРЖНЕВОЙ СИСТЕМЫ
Задание.Абсолютно жёсткий брус опирается на шарнирно неподвижную опору и прикреплён к двум стержням с помощью шарниров (рис. 1). Требуется: найти усилия и напряжения в стержнях, выразив их через силу Q; найти допускаемую нагрузку 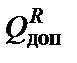 , приравняв большее из напряжений в двух стержнях расчетному сопротивлению R = 160 МПа; найти допускаемую нагрузку
, приравняв большее из напряжений в двух стержнях расчетному сопротивлению R = 160 МПа; найти допускаемую нагрузку 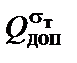 по предельному равновесию, если предел текучести
по предельному равновесию, если предел текучести 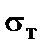 = 240 МПа; сравнить полученные величины допускаемых нагрузок.Данные взять из табл. 1.
= 240 МПа; сравнить полученные величины допускаемых нагрузок.Данные взять из табл. 1.
Таблица 1
| № строки | № схемы | A, см2 | a , м | b , м | c , м |
| | | | 2,1 | 2,1 | 1,1 |
| | | | 2,2 | 2,2 | 1,2 |
| | | | 2,3 | 2,3 | 1,3 |
| | | | 2,4 | 2,4 | 1,4 |
| | | | 2,5 | 2,5 | 1,5 |
| | | | 2,6 | 2,6 | 1,6 |
| | | | 2,7 | 2,7 | 1,7 |
| | | | 2,8 | 2,8 | 1,8 |
| | | | 2,9 | 2,9 | 1,9 |
| | | | 3,0 | 3,0 | 2,0 |
| | е | д | а | б | в |
Методические указания
Перед решением задачи необходимо сосчитать количество неизвестных сил, действующих на абсолютно жёсткий брус, и число независимых уравнений равновесия этого бруса. Если неизвестных больше числа уравнений статики, то задача будет статически неопределимой, и для её решения, кроме уравнений равновесия, потребуется составить ещё уравнения деформаций.
Для определения двух неизвестных усилий в стержнях следует составить систему уравнений, состоящую из одного уравнения статики и одного уравнения совместности деформаций.
Для ответа на третий вопрос задачи следует иметь в виду, что в одном из стержней напряжение больше, чем в другом; условно назовем этот стержень первым. При увеличении нагрузки напряжение в первом стержне достигнет предела текучести раньше, чем во втором. Когда это произойдет, напряжение в первом стержне перестанет расти и будет оставаться равным 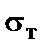 . Отсюда находим усилие в первом стержне:
. Отсюда находим усилие в первом стержне:
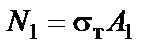 .
.
При дальнейшем увеличении нагрузки напряжение и во втором стержне достигнет предела текучести:
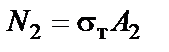 .
.
Написав уравнение статики и подставив в него значения усилий N1 и N2, найдем из этого уравнения предельную грузоподъемность 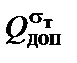 .
.
Пример 1. Абсолютно жёсткий брус опирается на шарнирно неподвижную опору и прикреплён к двум стержням с помощью шарниров(рис. 1, а). Требуется: найти усилия и напряжения в стержнях, выразив их через силу Q;найти допускаемую нагрузку 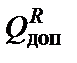 , приравняв большее из напряжений в двух стержнях расчетному сопротивлению R = 210 МПа; найти допускаемую нагрузку
, приравняв большее из напряжений в двух стержнях расчетному сопротивлению R = 210 МПа; найти допускаемую нагрузку 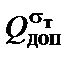 по предельному равновесию, если предел текучести
по предельному равновесию, если предел текучести 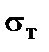 = 240 МПа; сравнить допускаемые нагрузки.
= 240 МПа; сравнить допускаемые нагрузки.
Дано: A = 10 cм2; a = 1 м; b = 1,4 м; c = 1,6 м; k = 2.
Решение.
1. Рассмотрим геометрическую сторону задачи. Для этого покажем схему деформирования заданной системы (рис. 1, б), обозначим буквами характерные точки абсолютно жёсткого бруса и пронумеруем стержни.
Абсолютно жёсткий брус под действием нагрузки Q повёрнется относительно шарнирной опорыS по часовой стрелке на угол a. Принимая угол a очень малым,из рис. 4, б видим, что первый стержень станет короче на величину 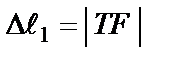 , а второй – длиннее на
, а второй – длиннее на 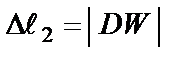 . Из подобия треугольников STF и SDW получим
. Из подобия треугольников STF и SDW получим
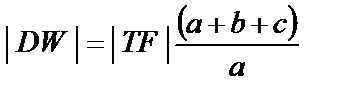 ,или
,или 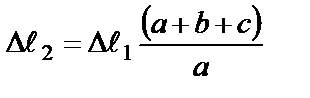 .(1)
.(1)
Уравнение (1) является уравнением совместности деформаций.
2. Рассмотрим статическую сторону задачи. Покажем все силы, действующие на абсолютно жёсткий брус (рис. 1, в). Направления усилий N1и N2определяем по схеме деформирования (рис. 1, б).
Неизвестными являются усилия N1,N2,а также две составляющие реакции опоры S. Общее число неизвестных равно четырём. Для решения задачи можно составить только три независимых уравнения равновесия, например:
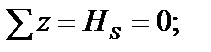 (2)
(2)
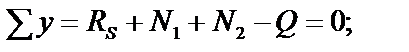 (3)
(3)
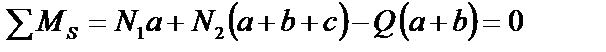 .(4)
.(4)
Следовательно, задача один раз статически неопределимая. В качестве дополнительного уравнения будем использовать уравнение совместности деформаций (1).
3. Рассмотрим физическую сторону задачи. В уравнении (1) выразим деформации через усилия по закону Гука
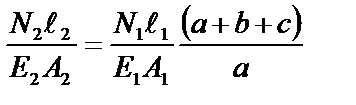 .(5)
.(5)
Подставив в (5) исходные данныеE1 = E2, A1 = kA,A2 = A,l1 = a,l2 = c,получим
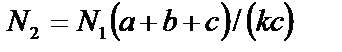 .(6)
.(6)
4. Для определения N1 и N2 решим совместно уравнения (4) и (6):
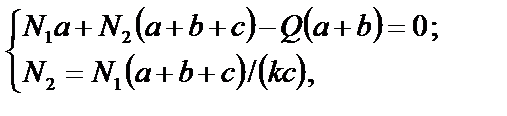
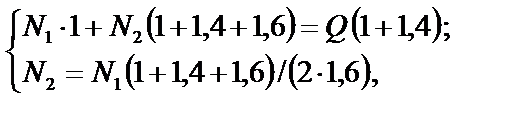
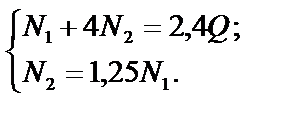
Окончательно имеем N1 = 0,4QиN2 = 0,5Q.
5. Составим выражения для напряжений в стержнях:
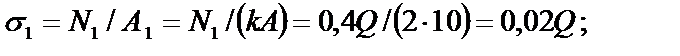
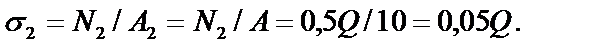
6. Сравним полученные напряжения 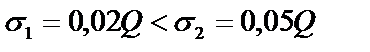 .
.
Напряжение во втором стержне получилось больше, чем в первом.
7. Определим допускаемую нагрузку из условия прочности наиболее напряженного стержня, в данном случае второго:
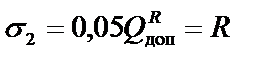 ;
; 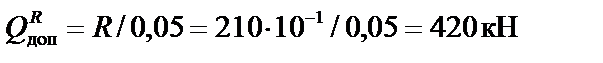 .
.
8. Рассмотрим предельное равновесие системы (рис. 1, г), полагая
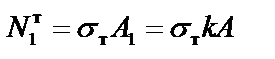 и
и
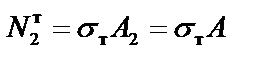
.
9. Составим и решим уравнение равновесия:
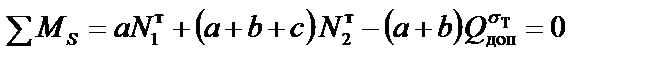 ;
;
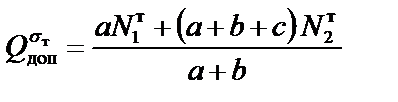 ;
;
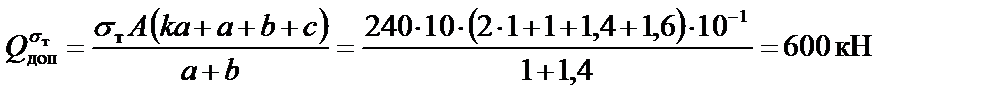 .
.
- Сравним полученные значения
 и
и 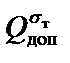 :
:
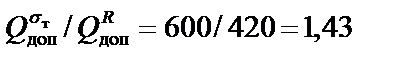 .
.
Вывод: допускаемая нагрузка, полученная по предельному равновесию, в 1,43 раза выше допускаемой нагрузки, найденной по расчётному сопротивлению.
Задача 2
РАСЧЕТ СТУПЕНЧАТОГО СТЕРЖНЯ
Задание.Ступенчатый стальной стержень (рис. 2) подвешен в вертикальном положении за верхний конец. При этом нижний конец стержня не доходит до основания на величину 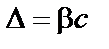 . Требуется (без учета собственного веса): установить, при какой величине силы Н зазор закроется; найти реакцию основания при заданном значении силы Н и построить для стержня эпюру продольных усилий; установить, на сколько градусов надо охладить стержень, чтобы реакция основания при заданном значении силы Н обратилась в нуль. Данные взять из табл. 2.
. Требуется (без учета собственного веса): установить, при какой величине силы Н зазор закроется; найти реакцию основания при заданном значении силы Н и построить для стержня эпюру продольных усилий; установить, на сколько градусов надо охладить стержень, чтобы реакция основания при заданном значении силы Н обратилась в нуль. Данные взять из табл. 2.
Методические указания
Для ответа на первый вопрос надо приравнять перемещение нижнего сечения стержня от искомых сил Н зазору D. Это перемещение равно сумме деформаций участков стержня от сил Н.
Для ответа на второй вопрос надо алгебраическую сумму перемещений нижнего сечения стержня от заданных сил Н и от реакции основанияприравнять зазору D.
Для ответа на третий вопрос надо приравнять перемещение нижнего сечения стержня от заданных сил Н сумме зазора и температурного укорочения стержня.
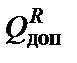 , приравняв большее из напряжений в двух стержнях расчетному сопротивлению R = 160 МПа; найти допускаемую нагрузку
, приравняв большее из напряжений в двух стержнях расчетному сопротивлению R = 160 МПа; найти допускаемую нагрузку 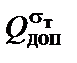 по предельному равновесию, если предел текучести
по предельному равновесию, если предел текучести 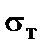 = 240 МПа; сравнить полученные величины допускаемых нагрузок.Данные взять из табл. 1.
= 240 МПа; сравнить полученные величины допускаемых нагрузок.Данные взять из табл. 1.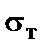 . Отсюда находим усилие в первом стержне:
. Отсюда находим усилие в первом стержне: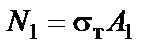 .
.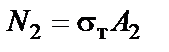 .
.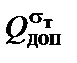 .
.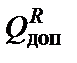 , приравняв большее из напряжений в двух стержнях расчетному сопротивлению R = 210 МПа; найти допускаемую нагрузку
, приравняв большее из напряжений в двух стержнях расчетному сопротивлению R = 210 МПа; найти допускаемую нагрузку 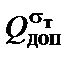 по предельному равновесию, если предел текучести
по предельному равновесию, если предел текучести 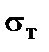 = 240 МПа; сравнить допускаемые нагрузки.
= 240 МПа; сравнить допускаемые нагрузки.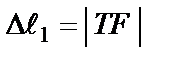 , а второй – длиннее на
, а второй – длиннее на 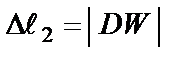 . Из подобия треугольников STF и SDW получим
. Из подобия треугольников STF и SDW получим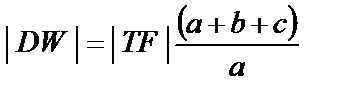 ,или
,или 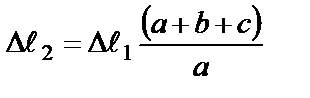 .(1)
.(1)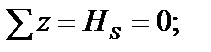 (2)
(2)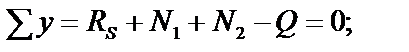 (3)
(3)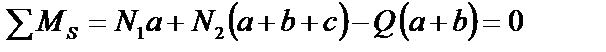 .(4)
.(4)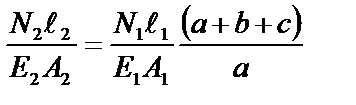 .(5)
.(5)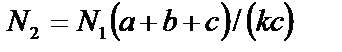 .(6)
.(6)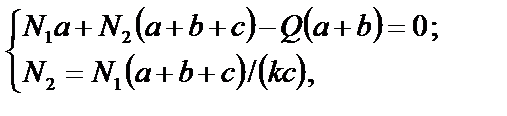
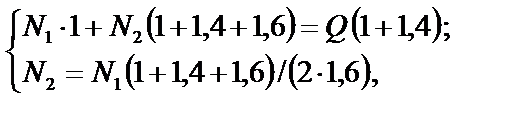
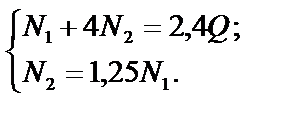
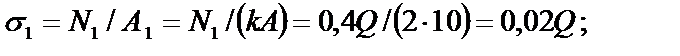
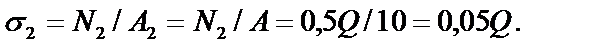
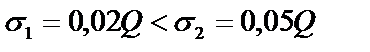 .
.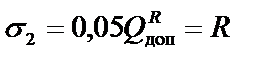 ;
; 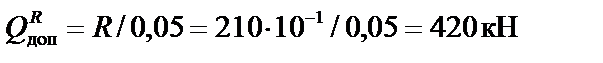 .
.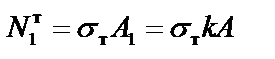 и
и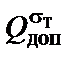
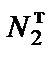
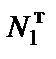
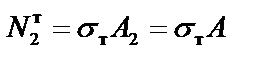 .
. 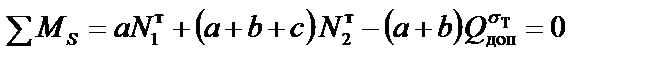 ;
;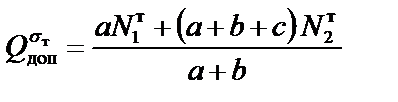 ;
;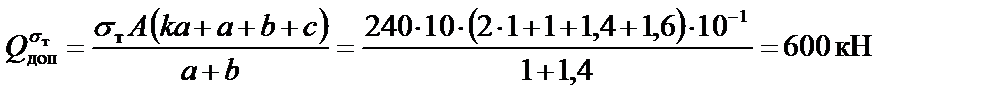 .
. и
и 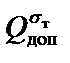 :
: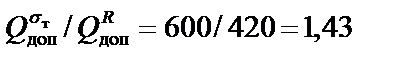 .
. . Требуется (без учета собственного веса): установить, при какой величине силы Н зазор закроется; найти реакцию основания при заданном значении силы Н и построить для стержня эпюру продольных усилий; установить, на сколько градусов надо охладить стержень, чтобы реакция основания при заданном значении силы Н обратилась в нуль. Данные взять из табл. 2.
. Требуется (без учета собственного веса): установить, при какой величине силы Н зазор закроется; найти реакцию основания при заданном значении силы Н и построить для стержня эпюру продольных усилий; установить, на сколько градусов надо охладить стержень, чтобы реакция основания при заданном значении силы Н обратилась в нуль. Данные взять из табл. 2.