Ема: Основні положення та означення комп`ютерної логіки. Частина 1. Функції алгебри логіки (булеві функції).

ЛАБОРАТОРНА РОБОТА 1

Мета роботи: Вивчення основних і похідних тотожностей булевої алгебри й їх застосування в процесі перетворення виразів у булевих алгебрах.

1 ОСНОВНІ ТЕОРЕТИЧНІ ВІДОМОСТІ

1.1 Поняття функції алгебри логіки

Функцією алгебри логіки (булевою функцією, БФ) f(x1, x2, ..., xn) від n змінних (аргументів) x1, x2, ..., xn називають таку функцію, що може приймати лише два значення, 0 і 1, та кожен із аргументів якої також може приймати лише два значення, 0 і 1.

Аргументи, від яких залежить булева функція, називають булевими або двійковими.

Область визначення будь-якої булевої функції f(x₁,…,x_n), що залежить від n змінних, складається з 2ⁿ кортежів (упорядкованих двійкових наборів значень змінних, від яких залежить функція), наприклад:

- область визначення будь-якої булевої функції від двох аргументів складається з 2² = 4 кортежів (00, 01, 10, 11);

- область визначення будь-якої булевої функції від трьох аргументів складається з 2³ = 8 кортежів (000, 001, 010, 011, 100, 101, 110, 111).

Дві булеві функції вважають різними, якщо вони відрізняються значенням хоча б на одному кортежі зі своєї області визначення.

Кількість різних булевих функцій від n аргументів дорівнює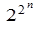

1.2 Способи задавання булевих функцій

Існує три основних способи задавання булевих функцій:

- табличний спосіб;

- вербальний (мовний) спосіб;

- аналітичний спосіб (за допомогою подання одних булевих функцій через інші).

При табличному способі задавання булевої функції:

- у лівій частині таблиці виписують усі кортежі із області визначення функції;

- у правій частині таблиці виписують значення, що приймає функція на тому чи іншому кортежі.

Такі таблиці називають таблицями істинності булевих функцій.

Для стандартизації процедури задавання булевих функцій за допомогою таблиць істинності, серед n-вимірних кортежів (n=1, 2, 3…) вводять природну (лексико-графічну) впорядкованість.

З даною метою, двійкові кортежі виду a = (a₁, ..., a_n) розглядають як подання цілих невід’ємних чисел виду a₁*2⁰+…+a_n*2^n-1 у двійковій системі числення (наприклад, кортежу (0,1,0,1,1) ­відповідає число 1*2⁰+1*2¹+0*2²+1*2³+0*2⁴=11).

Число, що відповідає певному набору (кортежу), називається номером набору (кортежу). Кортеж, що має номер і, називають і-тим кортежем.

Природний (лексико-графічний) порядок n-вимірних двійкових кортежів отримують, розташувавши їх у порядку зростання або спадання їх номерів.

Першим у розташуванні наборів у порядку зростання буде той набір, усі компоненти якого дорівнюють нулю, а останнім – той набір, усі компоненти якого дорівнюють одиниці.

Двійковий кортеж повністю визначається своїм номером і розмірністю, а тому, якщо розмірність кортежів задано, то їх можна ототожнювати з їхніми номерами.

Таким чином, будь-яка булева функція від n змінних може бути задана за допомогою таблиці істинності.

Загальний вид таблиці істинності для булевої функції від n змінних представлено у таблиці 1.1., яка містить 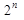рядків, а всі набори (x1, x2, ..., xn) розташовано в ній у порядку зростання їхніх номерів.

Таблиця 1.1

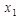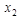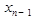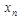		…			f(x1, x2, …, xn-1, xn)
…	…	… … … … …	…	…	f(0, 0, …, 0, 0) f(0, 0, …, 0, 1) f(0, 0, …, 1, 0) … f(1, 1, …, 1, 1)

Відзначимо, що, зі зростанням кількості аргументів, відбувається досить швидке зростання кількості булевих функцій.

Наприклад, існує вже 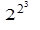= 2⁸ = 256 різних булевих функцій навіть від трьох аргументів, а число різних булевих функцій від п`яти змінних перевищує чотири мільйони.

Швидке зростання числа булевих функцій зі збільшенням числа аргументів фактично виключає можливість їх безпосереднього подання за допомогою таблиць.

В якості прикладу вербального (мовного) способу завдання булевих функцій наведемо два еквівалентних вербальних визначення кон’юнкції:

- кон’юнкція – булева функція двох аргументів, яка приймає значення одиниці тоді і тільки тоді, коли обидва аргументи приймають значення одиниці;

- кон’юнкція – булева функція двох аргументів, яка приймає значення нуля тоді і тільки тоді, коли хоча б один аргумент приймає значення нуля.

Розглянемо питання про аналітичне подання булевих функцій.

Відзначимо, що фундаментальне значення булевих функцій однієї та двох змінних в теорії булевих функцій полягає в тому, що з них може бути побудована будь-яка булева функція, від будь-якого числа змінних.

Засобом для такої побудови є суперпозиція булевих функцій - підстановка одних булевих функцій замість аргументів в інші булеві функції.

Можливість зазначеної підстановки обумовлено тим, що, в силу визначення, області визначення булевих функцій та області значень їхніх аргументів співпадають між собою.

Використовуючи суперпозицію, можна аргументами кожної з булевих функцій однієї та двох змінних вважати довільні булеві функції.

Тим самим булеві функції однієї та двох змінних можна розглядати не як функції, а як операції на множині всіх булевих функцій.

За допомогою цих операцій можуть бути побудовані різноманітні алгебри булевих функцій.

Булевою алгеброю (БА)називають множину булевих функцій, над якою визначені операції {Ú, Ù,` }.

У булевій алгебрі розглядають різноманітні вирази, що утворюються за допомогою операцій алгебри з констант 0, 1 та змінних, під якими розуміють довільні булеві функції (зокрема, звичайні двійкові змінні).

Порядок виконання операцій у булевій алгебрі є наступним: заперечення; кон’юнкція; диз’юнкція.

Наявність у виразі дужок змінює звичайний порядок виконання операцій: спочатку виконуються операції в дужках.

Будь-який вираз у зазначених алгебрах представляє собою деяку булеву функцію і, в свою чергу, може бути позначений однією літерою.

Два вирази в булевій алгебрі називають тотожніми, якщо, при підстановці в дані вирази конкретних двійкових наборів, представлені вказаними виразами булеві функції приймають однакові значення.

1.3 Особливості булевих функцій від однієї змінної

Згідно з вище сказаним, існує 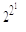= 4 різні булеві функції одного аргументу, що мають наступне табличне подання:

x	f0(x)	f1(x)	f2(x)	f3(x)

Булеві функції одного аргументу мають наступні аналітичні подання:

- f₀ (x) = 0 - константа 0;

- f₁(x) = x - тотожна функція;

- f₂(x) = /x - інверсія (заперечення) змінної x;

- f₃(x) = 1 - константа 1.

1.4 Особливості булевих функцій від двох змінних

Згідно з вище сказаним, кількість різних булевих функцій від двох змінних дорівнює 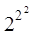= 16. Наведемо для них зведену таблицю істинності:

Наведені вище булеві функції двох змінних пронумеровано таким чином, що номер функції, записаний в двійковій системі числення, дає послідовність значень відповідної функції.

Наприклад, двійковому запису 13₁₀=1101₂ відповідає функція f₁₃(x,y), яка приймає наступні значення: f₁₃(0,0) = 1, f₁₃(0,1) = 1, f₁₃(1,0) = 0, f₁₃(1,1) = 1.

Деякі з булевих функцій двох змінних, наведених у таблиці, мають спеціальну назву та позначення.

Розглянемо зазначені спеціальні функції окремо, згрупувавши попарно за таким принципом, що кожна булева функція пари буде являти собою заперечення іншої булевої функції даної пари:

f0(x,y)=0, f15(x,y) = 1	-	тотожний нуль, тотожна одиниця
f1(x,y) = x * y = x Ù y = x & y = xy, f14(x,y)=	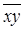-	кон’юнкція, штрих Шефера
f7(x,y) = х Ú у, f8(x,y)=x ¯ y= /(x Ú у)	-	диз’юнкція, стрілка Пірса (функція Веба)
f13(x,y) = x ® y, f2(x,y) = /(x ® y)	-	імплікація, заперечення імплікації
f11(x,y)= у ® х, f4(x,y)= /(y ® х)	-	антиімплікація, заперечення антиімплікації
f9(x, y) = x <=> y, f6(x,y)=х Å у	-	еквівалентність, додавання по модулю 2
f3(x,y) = x, f12(x,y) = /x	-	тотожна функція щодо х, заперечення х
f5(x,y) = y, f10(x,y)= /y	-	тотожна функція щодо y, заперечення y

1.5 Елементарні булеві функції

Елементарними булевими функціями називають одинадцять наведених нижче булевих функцій:

f1(x) = 0	-	константа 0;
f2(x) = 1	-	константа 1;
f3(x) = x	-	тотожна функція;
f4(x) = /x	-	заперечення x;
f5(x,y) = xy = x ˄ y = x & y	-	кон’юнкція x і y;
f6(x, y) = x ˅ y	-	диз'юнкція x і y;
f7(x, y) = x => y	-	імплікація x і y;
f8(x, y) = x <=> y	-	еквівалентність x і y;
f9(x, y) = x Å y	-	додавання x і y по mod 2;
f10(x, y) = x | y	-	функція Шефера (штрих Шефера);
f11(x, y) = x ↓ y	-	функція Пірса (стрілка Пірса).

Указані вище елементарні булеві функції f1 — f11 задаються таблицями істинності, зведеними разом до таблиці 1.2.

Таблиця 1.2

x

y

f1

f2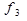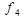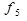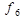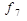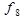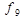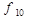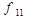

Визначення формули алгебри логіки є наступним:

1) кожна елементарна булева функція є формулою алгебри логіки;

2) якщо деякий логічний вираз є формулою алгебри логіки, то його логічне заперечення теж є формулою алгебри логіки;

3) якщо деякі логічні вирази η і μ є формулами алгебри логіки, то логічні вирази η ˅ μ, η ˄ μ, η => μ, η <=> μ, η Å μ, η | μ, η ↓ μ теж є формулами алгебри логіки;

4) будь-які логічні вирази, побудовані відповідно наведеним вище правилам 1-3, є формулами алгебри логіки.

З метою спрощення запису формул алгебри логіки, для операції кон’юнкції було встановлено сильніший пріоритет за інші логічні операції (якщо в формулі відсутні дужки, то спочатку виконується операція кон’юнкції).

Дві формули алгебри логіки називають рівнозначними (рівносильними, тотожніми), якщо вони визначають одну булеву функцію.

Запис η = μ буде означати, що формули алгебри логіки η і μ є рівносильними.

Формула алгебри логіки називається тавтологією (тотожно дійсною), якщо вона при будь-яких значеннях змінних приймає дійсне значення.

Формула алгебри логіки називається протиріччям (тотожно неправильною), якщо вона при будь-яких значеннях змінних приймає неправильне значення.

Формула алгебри логіки називається здійсненною, якщо знайдеться такий набір значень змінних, при якому її значення є дійсним.

Відзначимо, що засобом для встановлення справедливості основних тотожностей булевої алгебри служить перевірка рівності виразів, які розташовано в лівій і правій частині тотожності, на всіх наборах двійкових значень змінних, що входять в дані вирази.

Перелік найважливіших законів алгебри логіки, що є рівнозначностями (рівносильностями, тотожностями), наведено нижче:

1)	х = х	-	закон тотожності;
2)	х ˄/x = 0	-	закон протиріччя;
3)	x ˅ /x = 1	-	закон виключення третього;
4)	//x = x	-	закон подвійного заперечення;
5) 6)	x ˄ x = x, x ˅ x = x	- -	закон ідемпотентності для кон`юнкції; закон ідемпотентності для диз`юнкції;
7) 8)	x ˄ y = y ˄ x, x ˅ y = y ˅ x	- -	закон комутативності для кон`юнкції; закон комутативності для диз`юнкції;
9) 10)	x(y ˅ z) =xy ˅ xz, x ˅ yz =(x ˅ y)( x ˅ z)	- -	перший дистрибутивний закон; другий дистрибутивний закон;
11) 12)	x(yz) = (xy)z = xyz, x˅(y˅z) = (x˅ y)˅ z = x˅ y ˅ z	- -	закон асоціативності для кон`юнкції; закон асоціативності для диз`юнкції;
13) 14)	/(xy) = /x ˅ /y, /(x ˅ y) = /x ˄ /y	- -	закон де Моргана для кон`юнкції; закон де Моргана для диз`юнкції;
15) 16) 17) 18) 19) 20)	x ˄ 1 = x, x ˄ 0 = 0, x ˅ 0 = x, x ˅ 1 = 1, /0 = 1, /1 =0,	-	закони тотожності для констант;
21) 22)	x(x ˅ y) = x, x ˅ xy = x	- -	закон поглинання для кон`юнкції; закон поглинання для диз`юнкції;
23) 24)	(x ˅ y)(/x ˅ y) = y, xy ˅ /xy = y	-	закони склеювання.

Із основних тотожностей булевої алгебри можуть бути виведені нові тотожності, що називаються похідними.

Відзначимо наступні найважливіші похідні рівнозначності алгебри логіки:

25)	x => y = /x ˅ y
26)	x <=> y = xy ˅ /(xy)
27)	x Å y = x/y ˅ /xy
28)	x | y = /x ˅ /y
29)	x ↓ y = /x ˄ /y
30)	xy = /( /x ˅ /y)
31)	x ˅ y = /(/x ˄ /y)

Різниця між основними та похідними тожностями є умовною.

Для того, щоб підкреслити те, що мова йде не про основні, а про похідні тотожності, замість маленьких літер можна застосовувати в них великі латинські літери.

У загальному випадку, як для основних, так і для похідних тотожностей можна вважати наступне:

- літери, з яких складаються тотожності, є довільними виразами булевої алгебри;

- будь-яку похідну тотожність можна доводити так само, як і основні тотожності, тобто використовувати визначення тотожності виразів у булевій алгебрі.

Як приклад, який ілюструє сказане, розглянемо наступні тотожності:

- тотожність (21) - X*(XÚY) = X - закон поглинання для кон’юнкції;

- тотожність (22) - XÚX*Y = X - закон поглинання для диз'юнкції.

Доказ тотожності (21) є наступним:

X*(XÚY) =¹⁷ (XÚ0)*( XÚY) =¹⁰ XÚ0*Y =⁸ XÚY*0=¹⁶ XÚ0=¹⁷ X .

Тотожність 22 доводиться за допомогою наступного ланцюжку рівностей:

XÚX*Y =¹⁵ X*1Ú X*Y =⁹ X*(1ÚY) =⁸ X*(Y Ú1) =¹⁸ X*1=¹⁵ X.

Відзначимо, що поряд зі знаками “=” проставлено номери тотожностей, що застосовувалися на відповідних кроках доведення.

Тотожності (21) і (22) є справедливими при будь-яких значеннях X та Y.

Зокрема, тотожність (21) є справедливою при Y = 0, а тотожність (22) - при Y = 1.

Підставивши вказані величини у відповідні тотожності, отримаємо:

- тотожність (5) (закон ідемпотентності для кон`юнкції) - X * X = X;

- тотожність (6) (закон ідемпотентності для диз`юнкції) - X Ú X = X.

Також має місце тотожність XÚ /X*Y = XÚY, оскільки:

XÚ /X*Y =¹⁰ (XÚ /X)*(XÚY) =³ 1*(XÚY)⁷ = (XÚY)*1 =¹⁵ XÚY.

Наведені доведення основних і похідних тотожностей припускають узагальнення на випадок будь-якої кількості змінних, від яких залежать ліві та праві частини зазначених тотожностей.

Зокрема, за допомогою математичної індукції, з тотожностей (5-6) і (15-18) легко виводиться наступні твердження:

- кон’юнкція або диз’юнкція будь-якого числа однакових елементів X дорівнює X;

- якщо видалити з довільної кон’юнкції всі елементи, що дорівнюють 1, то величина кон’юнкції не зміниться;

- якщо в кон’юнкції хоча б один із елементів дорівнює 0, то і вся кон’юнкція теж дорівнює 0;

- якщо видалити з довільної булевої функції ті диз’юнктивні елементи, що дорівнюють 0, то величина диз’юнкції не зміниться;

- якщо хоча б один із елементів диз'юнкції дорівнює 1, то вся диз'юнкція теж дорівнює 1.

Узагальнення правил де Моргана (13-14) приводить до наступних тверджень:

- твердження (20) – /(X₁ * X₂ *… * X_m) = /X₁ Ú /X₂ Ú … Ú /X_m);

- твердження (21) – /(X₁ Ú X₂ Ú … Ú X_m) = /X₁ * /X₂ * … * /X_m);

Також важливо відзначити наступне: якщо до деякого виразу булевої алгебри X застосовано більше, ніж одну операцію заперечення, то, не змінюючи тих значень, які приймає вираз X, можна виключити будь-яке парне число зазначених операцій.

риклади

Приклад 1. Визначити, чи є тавтологією формула

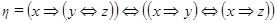
Зазтосуємо табличний спосіб визначення тавтології:

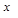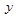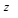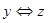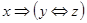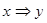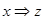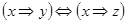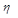Застосуємо також аналітичний спосіб визначення тавтології:

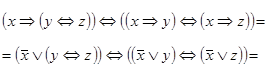
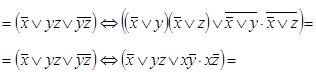
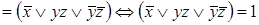
Приклад 2. Визначити, чи є рівносильними наступні формули:

;

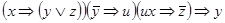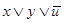
Виконаємо визначення рівносильності наведеним нижче аналітичним способом:

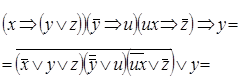
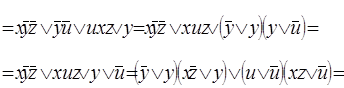
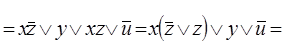
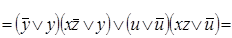
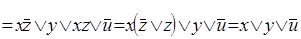
Виходячи з наведеного вище доведення, задані формули є рівносильними.

Приклад 3. Спростити формулу .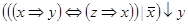

Виконаємо спрощення формули в наступний спосіб:

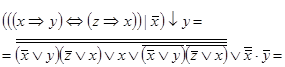
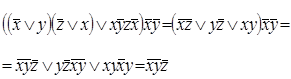
Приклад 4. Розв'язати рівняння .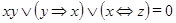

Указане рівняння є рівносильним наступній системі рівнянь:

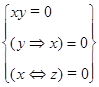
Із аналізу першого рівняння системи очевидно, що його розв`язками можуть бути наступні три пари значень:

- (x = 0; y = 0);

- (x = 0; y = 1);

- (x = 1; y = 0).

При підстановці вказаних вище пар значень до другого рівняння системи, легко визначити, що воно буде істинним лише для одного розв`язку, а саме:

- (x = 0; y = 1).

Підставляючи значення x, отримане на попередньому кроці, до третього рівняння системи, легко побачити, що єдиним значенням z може бути z = 1.

Отже, розв'язком початкового рівняння 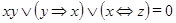є наступна сукупність значень: ( ; ; ).

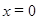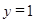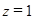2 КОНТРОЛЬНІ ПИТАННЯ

1. Дати визначення поняттю функції алгебри логіки (булевої функції).

2. Пояснити, як можна задати булеву функцію за допомогою таблиці істинності.

3. Назвати ті булеві функції, що належать до категорії елементарних.

4. Сформулювати поняття формули алгебри логіки.

5. Який пріоритет має логічна операція кон’юнкції ?

6. Дати визначення поняттю рівносильних формул алгебри логіки.

7. Які рівнозначності (закони) алгебри логіки відносять до категорії найважливіших ?

8. Пояснити основну відмінність між тими формулами алгебри логіки, що називаються:

а) тавтологією;

б) протиріччям;

в) здійсненною формулою.

9. Навести приклади доказу формул алгебри логіки, що є:

а) тавтологіями;

б) рівносильними формулами.

10. Навести приклади:

а) спрощення логічної формули;

б) розв'язування логічного рівняння.

3 ІНДИВІДУАЛЬНІ КОНТРОЛЬНІ ЗАВДАННЯ

Завдання 1 Побудувати таблицю істинності для однієї з наступних формул:

1) ;

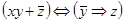2) ;

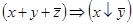3) ;

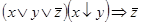4) ;

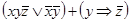5) ;

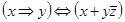6) ;

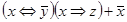7) ;

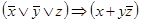8) ;

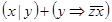9) ;

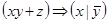10) .

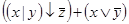Завдання 2. Без побудови таблиць істинності довести, що одна з наступних формул є тавтологією:

1) ;

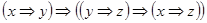2) ;

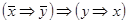3) ;

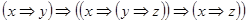4) ;

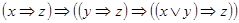5) ;

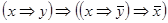6) ;

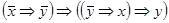7) ;

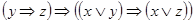8) ;

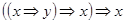9) ;

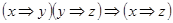10) .

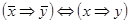Завдання 3. Без побудови таблиць істинності довести, що одна з наступних формул є протиріччям:

1) ;

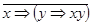2) ;

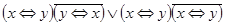3) ;

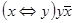4) ;

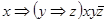5) ;

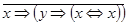6) ;

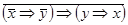7) ;

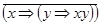8) ;

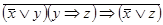9) ;

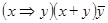10) .

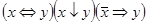Завдання 4. Розв'язати одне з наступних логічних рівнянь:

1) ;

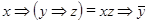2) ;

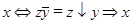3) ;

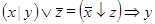4) ;

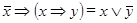5) ;

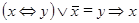6) ;

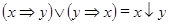7) ;

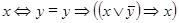8) ;

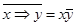9) ;

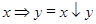10) .

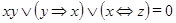Завдання 5. Спростити один із наступних логічних виразів:

1) ;

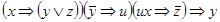2) ;

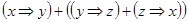3) ;

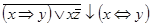4) ;

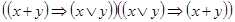5) ;

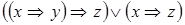6) ;

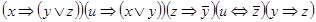7) ;

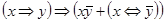8) ;

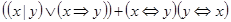9) ;

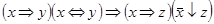10) .

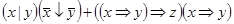Додаток А

Вимоги до оформлення, захисту та оцінювання

лабораторних робіт

Під час захисту лабораторної роботи, студент повинен здійснити:

− коротке викладення теоретичних основ і змісту визначальних етапів виконання роботи;

− демонстрацію результатів роботи;

− відповіді на питання викладача;

− подання підсумкового звіту про виконання роботи.

Звіт з лабораторної роботи повинен містити такі складові частини:

− титульний аркуш (зразок оформлення знаходиться далі, в Додатку Б);

− формулювання теми та мети лабораторної роботи;

− постановка індивідуального контрольного завдання на лабораторну роботу;

− покроковий опис ходу виконання роботи;

− опис результатів, отриманих у процесі виконання роботи;

− висновки;

− перелік використаної літератури.

Звіт про виконання лабораторної роботи може бути оформлений у наступній формі:

− письмовий (рукописний, друкований, електронний тощо);

− усний (доповідь, прокоментований показ на комп’ютері, озвучений слайдовий показ тощо);

− письмово-усний.

Електронний, усний і письмово-усний варіанти звіту припускаються тільки за дозволом викладача в тому разі, якщо студент вільно володіє темою та здатен доповісти її лаконічно, дохідливо та наочно в усній формі.

оцінку за виконання лабораторної роботи виставляють, згідно з існуючими положеннями, за однією з наведених нижче шкал, із наступним переведенням у виміри двох інших шкал:

− за національною шкалою, тобто за чотирибальною системою („відмінно/5”, „добре/4”, „задовільно/3”, „незадовільно/2”);

− за європейською шкалою ECTS, тобто за семибальною системою (“відмінно/A”, “добре/B,C”, “задовільно/D,E”, “незадовільно/FX,F”);

− за стобальною шкалою ХНТУ.

Основними критеріями оцінювання лабораторної роботи є:

− повнота та правильність виконання завдань;

− здатність студента до творчого застосування набутих ним знань, умінь і навичок (диференціації, інтеграції та уніфікації знань; застосування правил, методів, принципів і законів у конкретних ситуаціях; інтерпретації схем, графіків, діаграм; встановлювання різниці між причинами та наслідками; аналізу та оцінювання фактів і подій, прогнозування очікуваних результатів від прийнятих рішень тощо);

− здатність студента викладати матеріал на папері логічно, послідовно, з дотриманням вимог ЄСКД та ЄСТД.

При перевірці результатів виконання лабораторної роботи, виставляють диференційовану оцінку згідно з наступними вимогами:

− „відмінно” виставляють у тому разі, якщо студент виявив: всебічні, систематизовані, глибокі знання програмного матеріалу; вміння вільно виконувати завдання; засвоєння основної та додаткової літератури, що передбачена програмою, на рівні творчого використання;

− „добре”виставляють у тому разі, якщо студент виявив: повне знання програмного матеріалу; вміння виконання завдань; засвоєння основної літератури, що передбачена програмою, на рівні аналогічного відтворення;

− „задовільно”виставляють у тому разі, якщо студент виявив: повне знання основного програмного матеріалу в обсязі, що є необхідним для подальшого навчання та роботи; здатність упоратися з виконанням завдань, які передбачено програмою, на рівні репродуктивного відтворення.

Виконання лабораторної роботи на найвищий бал (оцінку “Відмінно/5/A”) передбачає обов`язкову наявність у звіті з лабораторної роботи елементів творчої роботи над матеріалом (порівняльного огляду, аналізу, формулювання та обгрунтування раціональних пропозицій, створення презентаційних матеріалів тощо), наведення прикладів практичного використання технологій комп'ютерної логіки.

Рекомендовано наступні види завдань творчої та практичної спрямованості:

− проаналізувати приклади ефективного використання технологій комп'ютерної логіки в комп'ютерній підтримці підприємств (організацій, установ) на основі відомостей із фундаментальної та періодичної літератури, власного досвіду;

− проаналізувати поточний стан і розробити пропозиції щодо підвищення ефективності використання технологій комп'ютерної логіки в комп'ютерній підтримці конкретного підприємства (організації, установи) за місцем проходження практики (місцем проживання, роботи тощо).

Виконання лабораторної роботи на оцінку “Добре/4/B,C”) передбачає розкриття поставленого завдання з наведенням прикладів практичного використання операційної системи.

Виконання лабораторної роботи на оцінку “Задовільно/3/D,E”) передбачає достатність розкриття поставленого завдання на основі репродуктивного відтворення матеріалів із запропонованого переліку літератури.

Таблиця А.1

Правила переведення балів внутрішньої 100-бальної шкали ХНТУ

в національну та європейську шкали

№ з/п	Оцінка за шкалою МОН України	Оцінка за національною шкалою	Оцінка за шкалою ECTS	Пояснення оцінки за шкалою ECTS
	90-100	Відмінно (5)	А	excellent	відмінно – відмінне вико- нання лише з незначною кількістю помилок
	75-89	82-89	Добре (4)	В	very good	дуже добре – вище середнього рівня з кількома помилками
	75-81	С	Good	добре – в загальному вірне виконання з певною кіль- кістю суттєвих помилок
	60-74	67-74	Задовільно (3)	D	satisfactory	задовільно – непогано, але зі значною кількістю недоліків
	60-66
E	sufficient	достатньо – виконане за- вдання задовольняє міні-мальним критеріям
	1-59	35-59	Незадовільно (2)	FX	fail (із правом перескладання)	незадовільно з можливістю повторного складання
	1-34
F	fail (повторний курс)	незадовільно з обов’язковим повторним курсом

Додаток Б

ЗРАЗОК ОФОРМЛЕННЯ ТИТУЛЬНОГО АРКУША

ЗВІТУ ПРО ВИКОНАННЯ ЛАБОРАТОРНОЇ РОБОТИ

МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
ХЕРСОНСЬКИЙ НАЦІОНАЛЬНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ
Кафедра інформаційних технологій
ЗВІТ З ЛАБОРАТОРНОЇ РОБОТИ 1
	з дисципліни „Комп'ютерна логіка”
	студента другого курсуденної форми навчання
	напряму підготовки 6.050102 “Комп’ютерна інженерія”
	з професійною орієнтацією “Комп’ютерні системи та мережі”
	галузі знань 0501 “Інформатика та обчислювальна техніка”
	факультету кібернетики та системної інженерії
	Іванова Петра Сидоровича
Дата проведення лабораторної роботи:		«» 2016р.
Дата подання звіту за графіком:		«» 2016р.
Дата подання звіту студентом:		____________________
Підпис студента:		____________________
Позначка викладача про результати та дату перевірки звіту:		____________________
		____________________
Відомості про викладача, що виконував перевірку звіту (прізвище, ініціали, посада, науковий ступінь, вчене звання):		Соколов А.Є., доцент кафедри інформаційних технологій ХНТУ, к.т.н., доцент
Підпис викладача, що виконував перевірку звіту :		_____________________
Херсон – 2016р.