Определение крутящего момента относительно центра тяжести сечения крыла

Крутящий момент относительно оси жесткости крыла возникает от нормальных к хорде составляющих погонной воздушной нагрузки 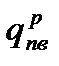, от массовых сил крыла 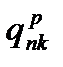, от массовых сил топлива 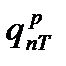и агрегатов, 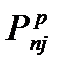расположенных в крыле. Погонный крутящий момент в любом сечении определится равенством:

,

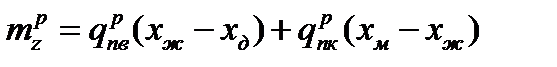здесь

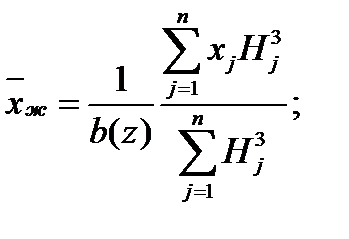
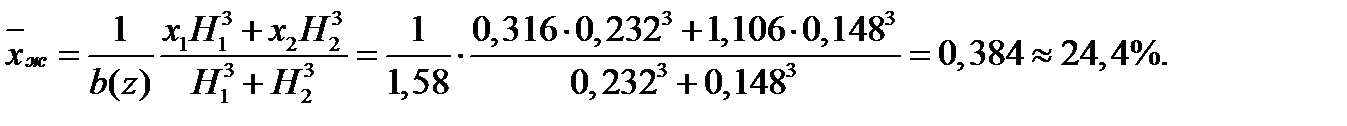
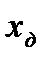- расстояние от носка до центра давления, которое находится для заданного расчетного случая с помощью формулы:

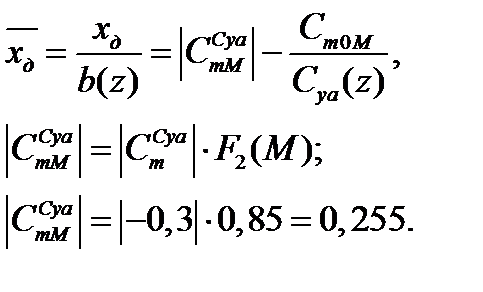
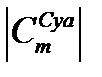-абсолютная величина производной 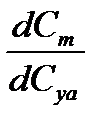без учета сжимаемости для профиля сечения – берется из профильной характеристики. Поправочный коэффициент 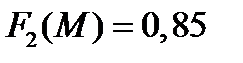определяется по значению числа Маха полета по [1, рис 1,3 в приложении 1.5].

При построении линии центров масс крыла можно принять х_м = (0,42...0,45)b(z).

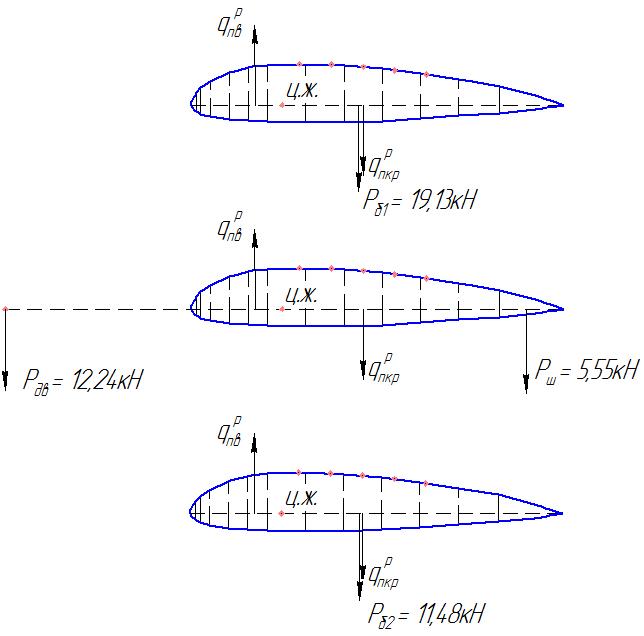
Рисунок 6 – К определению крутящего момента

Получим крутящий момент в любом сечении относительно центра жесткости:

,

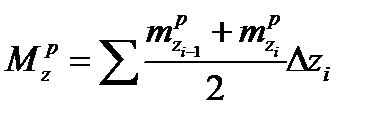На основании этих расчетов строятся эпюры 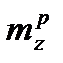_: и 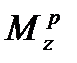по размаху крыла приведённые ниже.

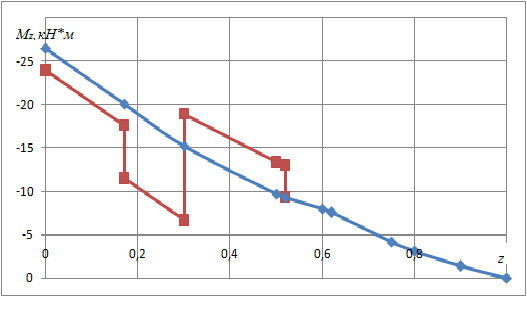
Рисунок 7 – Эпюра крутящего момента

Minenko 1402

ИСХОДНЫЕ ДАННЫЕ

X(I),см

0.000D+00 2.747D+00 1.580D+01 3.184D+01 4.482D+01

5.805D+01 7.126D+01 8.442D+01 9.480D+01 1.097D+02

1.097D+02 9.480D+01 8.442D+01 7.126D+01 5.805D+01

4.482D+01 3.352D+01 1.580D+01 2.747D+00

Y(I),см

0.000D+00 5.871D+00 1.339D+01 1.649D+01 1.693D+01

1.667D+01 1.576D+01 1.435D+01 1.298D+01 1.058D+01

-4.464D+00 -5.590D+00 -6.301D+00 -6.936D+00 -7.296D+00

-7.310D+00 -6.843D+00 -3.690D+00 -3.051D+00

F(I),см**2

3.200D-01 3.070D-01 3.410D-01 1.383D+01 3.190D-01

3.240D-01 3.240D-01 3.240D-01 3.240D-01 8.946D+00

4.323D+00 3.240D-01 3.240D-01 3.240D-01 3.240D-01

3.190D-01 8.970D+00 3.400D-01 3.000D-01

PHI0(I)

1.000D+00 1.000D+00 1.000D+00 1.000D+00 1.000D+00

1.000D+00 1.000D+00 1.000D+00 1.000D+00 1.000D+00

1.000D+00 1.000D+00 1.000D+00 1.000D+00 1.000D+00

1.000D+00 1.000D+00 1.000D+00 1.000D+00

Mx(кНм),Qy(кН)

1.102D+02 4.930D+01

E0,E1,E2

7.200D+04 7.200D+04 7.200D+04

ST,ST1,ST2

2.700D+02 2.700D+02 2.700D+02

SCR,SCR1,SCR2

1.868D+02 3.097D+02 2.910D+02

I1,I2,I3,I4

4 10 11 17

D1,D2,D3,D4

5.000D-01 5.000D-01 5.000D-01 5.000D-01

DEL1,DEL2

8.000D-01 5.000D-01

PSI1,PSI2,PSI3,PSI4

2.760D-01 4.140D-01 6.210D-01 4.480D-01

N= 20

РЕЗУЛЬТАТЫ ВЫЧИСЛЕНИЯ НОРМАЛЬНЫХ НАПРЯЖЕНИЙ

J-номер приближения для SIGMA(I) и PHI(I)

(J-1)- номер приближения для SIGMAr(I)

J=1

SIGMAr(I) в МПа, I=2,M

4.067D+01 -1.664D+02 -2.569D+02 -2.750D+02 -2.745D+02

-2.566D+02 -2.253D+02 -1.938D+02 -1.369D+02 2.646D+02

3.019D+02 3.259D+02 3.493D+02 3.653D+02 3.721D+02

3.651D+02 2.895D+02 2.788D+02

SIGMA(I),I=2,M

4.067D+01 -1.664D+02 -2.569D+02 -1.868D+02 -1.868D+02

-1.868D+02 -1.868D+02 -1.868D+02 -1.369D+02 2.646D+02

2.700D+02 2.700D+02 2.700D+02 2.700D+02 2.700D+02

2.700D+02 2.700D+02 2.700D+02

PHI(I),I=1,M

1.000D+00

1.000D+00 1.000D+00 1.000D+00 6.793D-01 6.805D-01

7.281D-01 8.291D-01 9.641D-01 1.000D+00 1.000D+00

8.943D-01 8.284D-01 7.730D-01 7.391D-01 7.257D-01

7.395D-01 9.325D-01 9.684D-01

Геометрические характеристики сечения крыла

Fr0(см**2),Xт,Yт(см)

4.091D+01 5.959D+01 6.361D+00

Irx(см**4)

5.804D+03

Угол ALFA в градусах

-1.125D+00

J= 20

SIGMAr(I) в МПа, I=2,M

1.512D+03 2.021D+02 -4.217D+02 -5.948D+02 -6.574D+02

-6.146D+02 -4.918D+02 -3.533D+02 -8.510D+01 2.330D+03

2.628D+03 2.824D+03 3.029D+03 3.191D+03 3.297D+03

3.311D+03 2.944D+03 2.944D+03

SIGMA(I),I=2,M

1.512D+03 2.021D+02 -3.097D+02 -1.868D+02 -1.868D+02

-1.868D+02 -1.868D+02 -1.868D+02 -8.510D+01 2.700D+02

2.700D+02 2.700D+02 2.700D+02 2.700D+02 2.700D+02

2.700D+02 2.700D+02 2.700D+02

PHI(I),I=1,M

1.000D+00

1.000D+00 1.000D+00 7.344D-01 3.141D-01 2.842D-01

3.039D-01 3.799D-01 5.288D-01 1.000D+00 1.159D-01

1.027D-01 9.561D-02 8.913D-02 8.461D-02 8.189D-02

8.154D-02 9.170D-02 9.170D-02

Геометрические характеристики сечения крыла

Fr0(см**2),Xт,Yт(см)

2.280D+01 6.446D+01 1.227D+01

Угол ALFA в градусах

-2.859D+00

РЕЗУЛЬТАТЫ ВЫЧИСЛЕНИЯ КАСАТЕЛЬНЫХ УСИЛИЙ

T(I) - касательное усилие на I-ом участке

обшивки крыла при простом изгибе

T(I) в Н/мм,I=1,M

-1.388D+01 -3.497D+01 -3.792D+01 5.487D+00 8.265D+00

1.108D+01 1.389D+01 1.669D+01 1.951D+01 5.586D+01

2.421D+00 -1.583D+00 -5.586D+00 -9.587D+00 -1.359D+01

-1.752D+01 3.012D+01 2.593D+01 2.223D+01

Нормальные напряжения в поясах лонжеронов

J=1

SIGMA1,SIGMA2,SIGMA3,SIGMA4

-2.569D+02 -1.369D+02 2.646D+02 2.700D+02

J= 2

SIGMA1,SIGMA2,SIGMA3,SIGMA4

-2.565D+02 -1.567D+02 2.700D+02 2.700D+02

J= 3

SIGMA1,SIGMA2,SIGMA3,SIGMA4

-2.559D+02 -1.639D+02 2.700D+02 2.700D+02

J= 4

SIGMA1,SIGMA2,SIGMA3,SIGMA4

-2.583D+02 -1.636D+02 2.700D+02 2.700D+02

J= 5

SIGMA1,SIGMA2,SIGMA3,SIGMA4

-2.623D+02 -1.597D+02 2.700D+02 2.700D+02

J= 6

SIGMA1,SIGMA2,SIGMA3,SIGMA4

-2.672D+02 -1.543D+02 2.700D+02 2.700D+02

J= 7

SIGMA1,SIGMA2,SIGMA3,SIGMA4

-2.728D+02 -1.480D+02 2.700D+02 2.700D+02

J= 8

SIGMA1,SIGMA2,SIGMA3,SIGMA4

-2.788D+02 -1.413D+02 2.700D+02 2.700D+02

J= 9

SIGMA1,SIGMA2,SIGMA3,SIGMA4

-2.852D+02 -1.343D+02 2.700D+02 2.700D+02

J= 10

SIGMA1,SIGMA2,SIGMA3,SIGMA4

-2.916D+02 -1.272D+02 2.700D+02 2.700D+02

J= 11

SIGMA1,SIGMA2,SIGMA3,SIGMA4

-2.980D+02 -1.203D+02 2.700D+02 2.700D+02

J= 12

SIGMA1,SIGMA2,SIGMA3,SIGMA4

-3.041D+02 -1.138D+02 2.700D+02 2.700D+02

J= 13

SIGMA1,SIGMA2,SIGMA3,SIGMA4

-3.097D+02 -1.054D+02 2.700D+02 2.700D+02

J= 14

SIGMA1,SIGMA2,SIGMA3,SIGMA4

-3.097D+02 -1.002D+02 2.700D+02 2.700D+02

J= 15

SIGMA1,SIGMA2,SIGMA3,SIGMA4

-3.097D+02 -9.564D+01 2.700D+02 2.700D+02

J= 16

SIGMA1,SIGMA2,SIGMA3,SIGMA4

-3.097D+02 -9.187D+01 2.700D+02 2.700D+02

J= 17

SIGMA1,SIGMA2,SIGMA3,SIGMA4

-3.097D+02 -8.784D+01 2.700D+02 2.700D+02

J= 18

SIGMA1,SIGMA2,SIGMA3,SIGMA4

-3.097D+02 -8.739D+01 2.700D+02 2.700D+02

J= 19

SIGMA1,SIGMA2,SIGMA3,SIGMA4

-3.097D+02 -8.641D+01 2.700D+02 2.700D+02

J= 20

SIGMA1,SIGMA2,SIGMA3,SIGMA4

-3.097D+02 -8.640D+01 2.700D+02 2.700D+02

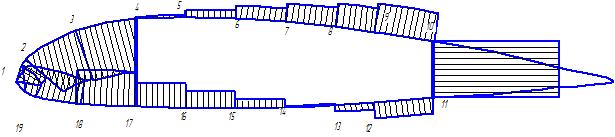
Рисунок 8 – Эпюра касательных напряжений в расчетном сечении крыла

Для оценки прочности воспользуемся формулой:

,

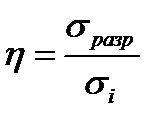где 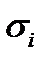- разрушающее напряжение в i-м лонжероне.

Для первого лонжерона в сжатой зоне:

,

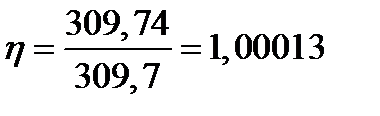для второго лонжерона в сжатой зоне:

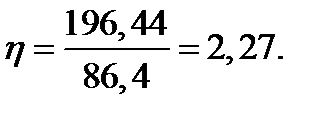
РАСЧЕТ ШАССИ