Устойчивость линейных САР. Признаки устойчивости. Запасы устойчивости линейных САР.

На любую систему автоматического регулирования всегда действуют различные внутренние и внешние возмущения, которые могут нарушить ее нормальную работу. Правильно спроектированная САР должна устойчиво работать при всех возмущениях. Определение устойчивости: под устойчивостью понимают способность системы возвращаться с определенной точностью к состоянию равновесия после устранения причин, выведенных систему из состояния равновесия.

Для пояснения смысла, понятия устойчивости положения равновесия системы, удобно воспользоваться следующим примером. Пусть имеется некоторая чаша, поставленная дном вниз (рис. 1).

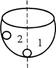
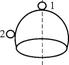
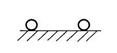
а) Устойчивая система б) Неустойчивая система в) Граница устойчивости

На дне чаши (а) в положении равновесия 1 находится тяжелый шарик, который приложенный внешней силой может быть отклонен в положение 2. В определенный момент времени, принимаемый за нулевой, внешняя сила убирается. Шарик, предоставленный сам себе, из положения 2 устремится вниз, и по инерции проскочит положение 1. Затем, достигнув наивысшего положения, уже справа от точки 1, шарик снова будет двигаться вниз. Совершив несколько колебательных движений, шарик из-за наличия сил сопротивления остановится с некоторой точностью в положении равновесия 1, т.е. согласно определению имеет место устойчивость положения равновесия для кратности обозначаемая литерой У.

В случае, когда чаша поставлена дном вверх (б). Шарик снова находится в положении равновесия 1 и если к нему не прикладывать никаких сил, то в этом положении он будет находиться сколь угодно долго. Если же некоторой внешней силой переместить шарик в положение 2, а затем убрать эту силу, то шарик удалится от положения 1 на бесконечно большое расстояние и никогда в него не вернется. Такое положение равновесия называется и обозначается .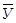

В третьем случае (в) изображено нейтральное положение равновесия или граница устойчивости. Если шарик, находящийся на горизонтальной поверхности в положении 1, с помощью внешней силы переместить в положение 2, а затем убрать эту силу, то шарик останется положении 2 до тех пор, пока к нему не будет приложена новая внешняя сила. Случай нейтрального положения равновесия, можно обнаружить и на рис. 1 а, если там не существует сил сопротивления. В этом случае шарик будет совершать незатухающие колебания вокруг положения равновесия 1.

Принцип устойчивости САР

Обратимся теперь к математической стороне вопроса. Любая система автоматического регулирования с входным сигналом (внешней силой) х и выходным сигналом z, имеющая передаточную функцию:

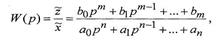(1)

может быть описана линейным неоднородным дифференциальным уравнением
п-го порядка с постоянными коэффициентам

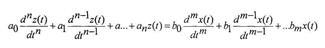(2)

Решение этого неоднородного уравнения z(t,)состоит из общего решения z_св(t)-свободная составляющая однородного дифференциального уравнения

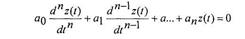(3)

и частного вынужденного решения z_вын (t)-вынужденная составляющая, т.е. то что остается после затухания свободной составляющей дифференциального уравнения z(t)=z_св(t) + z_вын(t).

Из определения устойчивости, данного выше, следует, что устойчивость САР устанавливают в ней, после того как устраняется внешняя сила, выведшая САР из состояния равновесия. Иными словами, устойчивость системы определяет переходный процесс z_св(t), т.е. решение однородного дифференциального уравнения . Таким образом, признаками устойчивости системы являются:

если ;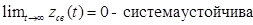

если ;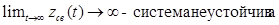

если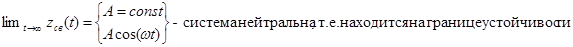

Дифференциальному уравнению (3) соответствует характеристическое уравнение 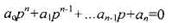(4)

корни, которых могут быть либо вещественными (в том числе нулевыми) либо комплексно-сопряженными (в том числе чисто мнимыми).

Решение дифференциального уравнения (3) как известно, имеет следующий вид 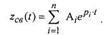(5)

где А, - постоянные интегрирования, определяемые параметрами системы и начальными условиями; р_i - корни характеристического уравнения (4.).

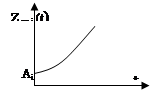Рассмотрим случаи, когда р_i –вещественные корни

а) пусть р_i = а_i , где а_i >0 корни положительные вещественные

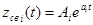, следовательно p_i >0 – система неустойчива

б) пусть p_i = -a_i , где a_i>0 корни отрицательные вещественные

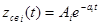, следовательно p_i <0 – система устойчива

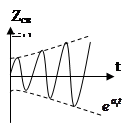в) пусть есть два комплексно сопряженных корня

p_i, _i+1 = a_i ± jβ_i , где a_i >0

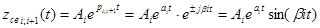- неустойчивая

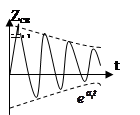г) p_i, _i+1 =- a_i ± jβ_i , где a_i >0

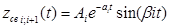
- устойчивая

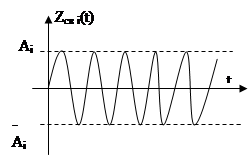д) корни мнимые – не содержат действительной части

a_i = 0. p_i,_i+1 = ±β_it (a_i=0)

z_{cв i, i+1}(t)= A_i sin β_it граница устойчивости -

e) p_i = 0 z_{св I} (t)= A_i

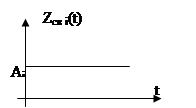- граница устойчивости

Рассмотрим все случаи на плоскости

P₁ - сл. (а); Р₂ – сл. (б); Р_к = 0 – сл. (е); Р_{е, у+1} – сл. (д)

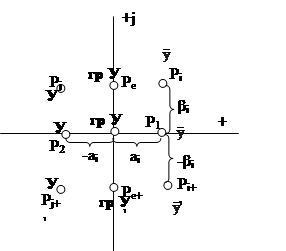
Признак устойчивости системы

Если все корни характеристического уравнения левые (либо отрицательные, либо имеют отрицательную вещественную часть), то система устойчива.

Если среди корней характеристического уравнения хотя бы один – правый, система - неустойчива.

Система находится на границе устойчивости, если кроме левых корней есть еще корни, расположенные на мнимой оси.

Расположение корней зависит от коэффициентов характеристического уравнения, а следовательно, от параметров системы. a₀pⁿ + … + a_n = 0.

Если К₂ > К₁ – корни сдвинутся вправо.

Если К₃> К₂ – может привести к неустойчивости системы. При переходе корня навстречу штриховке устойчивость уменьшается.

Чем больше коэффициент усиления, тем меньше устойчивость (в большинстве случаев).
К₃> К_гр>К₂>К₁. К_гр – параметр, при котором система выходит на границу устойчивости.

Система, у которой изменением параметра можно изменить устойчивость системы называется структурно-устойчивой системой; в противном случае, когда никакими изменениями параметров неустойчивую систему нельзя сделать устойчивой, называется структурно-неустойчивой системой.

Но корни характеристического уравнения можно вычислить только до 4 степени и вычисление их очень трудоемко.

Стодола – высказал условие, которое оказалось необходимым, но недостаточным.

Условие Стодола: Для устойчивости системы необходимо (но недостаточно), чтобы все коэффициенты характеристического уравнения были положительны (одного знака). Это условие будет необходимым и достаточным для уравнений 1 и 2 порядков.

Запасы устойчивости

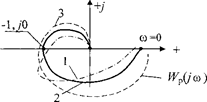Устойчивость является необходимым условием нормального функционирования САР. Если АФХ разомкнутой системы не охватывает критической точки (-1, j0), то САР в замкнутом состоянии устойчива (кривая 1 на рис. I), а если указанная АФХ проходит через т. (-1, j0), то замкнутая САР находится на границе устойчивости (кривая 2 на рис. I).

Отметим при этом, что чем ближе находится кривая 1 к критической точке (-1, j0), тем менее устойчивой становится замкнутая САР. Поскольку положение АФХ W_p(jω) на плоскости Гаусса определяется параметрами системы (коэффициентами усиления, постоянными времени и т.п. звеньев), то расположение кривых W_p(jω) вблизи притяжений точки может привести к ошибочным выводам об устойчивости САР. В самом деле, пусть в исходном состоянии параметры САР таковы, что отвечающая им кривая АФХ заняла положение 1. Однако, со временем в процессе эксплуатации параметры САР изменяются, и соответствующая этим измененным параметрам кривая W_p(jω) уже станет охватывать т. (-1,j0), т.е. займет положение 3. Это означает, что со временем, рассчитанная как устойчивая, САР станет неустойчивой.

Этой ситуации не возникнет, если САР работает не вблизи границе устойчивости. А в достаточном удалении от нее. Иначе говоря, САР должна обладать некоторым запасом устойчивости, обеспечивающим работоспособность ее в различных условиях эксплуатации.

Так как устойчивость замкнутой системы оценивается критерием Найквиста по расположению АФХ разомкнутой системы относительно критической точки, то в качестве меры оценки запаса устойчивости можно принять расстояние между АФХ W_p(jω) и критической точки (-1, j0). Но положение АФХ W_p(jω) на комплексной плоскости для каждого значения частоты ω характеризуется фазой и модулем. Именно поэтому вводят понятия запасов устойчивости те модулю (амплитуде) и фазе.

Под запасом устойчивости по амплитуде понимают линейное отстояние точки АФХ разомкнутой системы с фазой = -180⁰ от критической точки (-1;j0).

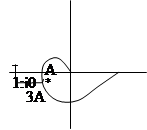
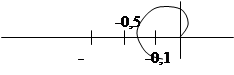
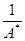- запас устойчивости по амплитуде. Для хороших систем (качественных) 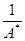= 2÷10.

С ростом К_уст – запас устойчивости

по амплитуде уменьшается.

Под запасом устойчивости по фазе понимаются угловое состояние точки АФХ разомкнутой системы с модулем =1 от критической точки -1;j0.

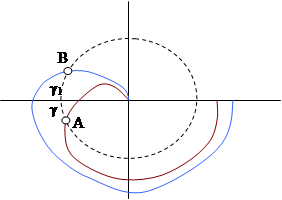
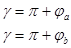
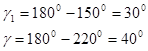
Для устойчивых систем ЗУФ положителен γ>0.

Для неустойчивых систем ЗУФ отрицателен γ₁>0.

С увеличением К_усил запас устойчивости по фазе уменьшается. Для хороших качественных систем γ =30⁰ ÷ 60⁰.