В общем виде обращение к функции

ОГЛАВЛЕНИЕ

Предисловие…………………………………………………….4

Глава 1. Краткие основы работы в MATLAB……………..5

1.1. Интерфейс. ………………………………………………………….5

1.2. Редактирование М-файлов ……………………………………8

1.3. Построение графиков……………………………………………12

1.4. Построение поверхности………………………………………13

1.5. Операции с матрицами. ……………………………………….14

1.6. Нелинейные уравнения и системы…………………………...15

1.7. Интегрирование…………………………………………………...16

Решение обыкновенных дифференциальных

уравнений и систем………………………………………18

1.9. Поиск экстремума функции одной переменной…………...21

1.10. Поиск экстремума функции нескольких переменной…..21

Глава 2. Одномерная оптимизация с

применением пакета MATLAB …………………..23

2.1. Метод сканирования……………………………………………...23

2.2. Метод чисел Фибоначчи…………………………………………29

2.3. Метод локализации экстремума……………………………...35

2.4. Метод обратного половинного шага………………………..43

2.5. Метод золотого сечения………………………………………..51

Глава 3. Двухмерная оптимизация с

применением пакета MATLAB……………………57

3.1. Метод сканирования……………………………………………...57

3.2. Метод Гаусса-Зейделя …………………………………………..61

3.3. Метод пробных движений ……………………………………..67

Предисловие

Методы оптимизации широко применяются в настоящее время при компьютерном моделировании и проектировании. Важной задачей является обучение навыкам реализации конкретных методов оптимизации на компьютерах с применением математических пакетов решения конкретных оптимизационных задач программ, например, MATLAB.

В учебном пособии представлены примеры решения задач одномерной и двумерной оптимизации c применением пакета MATLAB. С целью наилучшего понимания и усвоения методов оптимизации приводятся подробные коды программ, дана табличная и графическая интерпретация промежуточных и конечных результатов вычислений. Ограничение размерности рассматриваемых оптимизационных задач связано исключительно с необходимостью наилучшей интерпретируемостью результатов решений для случаев одномерного и двумерного поиска экстремумов.

Для контингента студентов, имеющих недостаточный опыт работы с пакетом MATLAB, в отдельной главе изложены его основные функциональные возможности. Приведенные в пособии коды программных модулей включают многочисленные комментарии и могут использоваться при решении практических задач оптимизации химико-технологических процессов.

Глава 1. Краткие основы работы в MATLAB

Интерфейс.

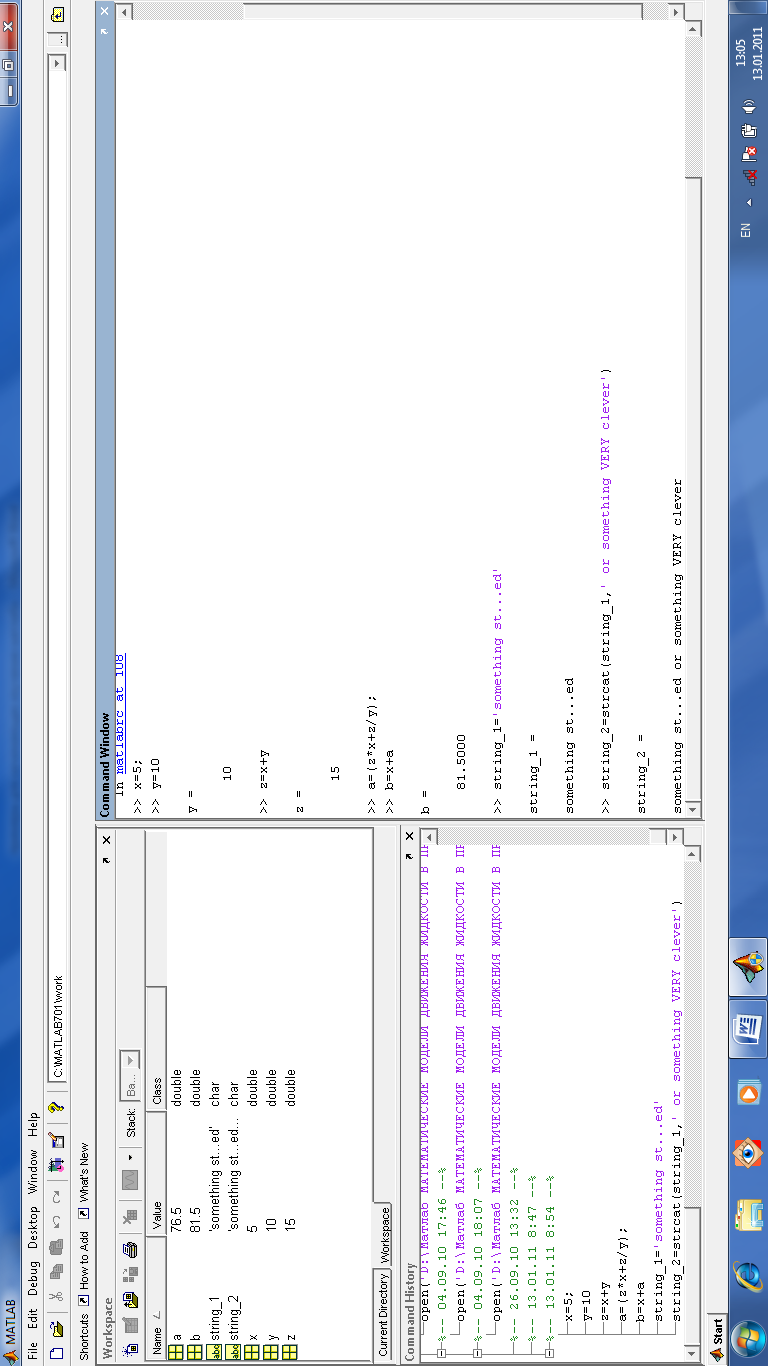
После запуска МАТЛАБ на экране появляется основное окно приложения (рис.1.1.). Оно содержит меню, панель инструментов и рабочую область (Commаnd Window).

Рис. 1.1. Интерфейс. Основное окно.

В рабочей области находится знак >> после которого расположен курсор. Эту строку называют командной строкой. В нее с клавиатуры вводятся команды. Нажатие Enter заставит выполнить команду и вывести результат в том же окне. (см. рис. 1.1.)

Так как текст в окне по мере работы смещается (уступает место новым командам и выводимым данным) то для просмотра выехавшей за окно части текста используют полосы прокрутки или клавиши Page Up, Page Down.

Клавиши ↑ и ↓ позволяют вернуть в командную строку ранее введенные команды или другую входную информацию (она вся обязательно автоматически хранится и всегда доступна). Кнопка ↑ помещает в командную строку предыдущую команду, а если еще раз ее нажать то еще предыдущую и так далее. Кнопка ↓ выводит команды (ранее набранные) в обратном порядке.

Видимая часть информации (то есть то что поместилось в окне) называется зоной просмотра, а командная строка зоной редактирования.

В зоне просмотра ничего нельзя исправить или ввести. Можно только выделить мышкой для копирования.

Если команда заканчивается ; то результат ее выполнения не отображается в командной строке. Иначе, то есть если строка не заканчивается на ; то результат сразу же после нажатия на Enter выводится в окне ниже этой команды. (см. выше на рис. 1.1)

Значения всех переменных, вычисленные в течение работы, сохраняются в специальной области памяти, называемой Workspace. (см. выше на рис. 1.1)

Определения всех переменных и функций и их последние перед закрытием программы значения можно сохранить на диск в файл с расширением .mat но само содержание Command Window при выключении МАТЛАБа не сохраняется никаким способом.

Примеры выполнения арифметических операций показаны на рис.1.1.

Для строк символов необходимо текст помещать в ‘одинарные кавычки’. Для сложения строк символов используется операция strcat, как показано на рис.1.1.

В главном меню (см. рис.1.1) следует обратить внимание на команду Desktop (настройка среды МАТЛАБ). При нажатии раскроется список, содержащий Desktop Layout который предлагает на выбор:

· Default устанавливает настройку принятую по умолчанию, то есть открывает окна Command Window, Workspace, Command History, Current Directory.

· Command Window Only открывает только окно Command Window.

· History and Command Window открывает соответствующие окна.

· All Tabbet показывает окно справки, окно управления М-файлами и внизу ярлычки рабочих окон, которые можно выбрать щелчком.

Также работа может осуществляться в программном режиме, то есть в командной строке указывается имя М-файла (файл с расширением .m), который содержит программу действий (алгоритм) и может рассматриваться как функция, то есть при указании его имени (без указания расширения) в командной строке выполняются запрограммированные в нем операции. (см.рис.1.2).

Как выгладит содержимое М-файла, см. рис.1.3.

Числовые переменные могут быть с плавающей точкой (тогда указывается порядок, например 6.4713e+003) или с фиксированной точкой (например 81.5000).

Текстовые комментарии начинаются со знака % (см.рис.1.2).

Все функции разделяются на встроенные и определенные пользователем. Встроенные, например, это y=sin(x); y=atan(x); y=exp(x); y=log(x) натуральный логарифм, а вот y=log10(x) десятичный логарифм, y=fix(x) округление до ближайшего целого в сторону нуля, y=floor(x) округление до ближайшего целого в сторону отрицательной бесконечности, y=ceil(x) округление до ближайшего целого в сторону положительной бесконечности, y=round(x) обычное округление

Массив задается так: ИМЯ_МАССИВА = НАИМЕНЬШ_ЭЛ-Т_МАСС : ШАГ_ИЗМЕН_ЭЛ-ТА_МАСС : НАИБОЛЬШ_ЭЛ-Т_МАСС ; (см. рис.1.2).

Обращение к элементу массива y=x_mas(2); где в скобках указывается порядковый номер (индекс) элемента массива (см. рис.1.2).

Редактирование М-файлов

«File»—«New»--«M-file» позволяет открыть окно Editor то есть Редактор М-файлов. В этом окне напечатать текст программы, которая должна быть выполнена, когда имя этого М-файла будет указано в командной строке в Command Window. Иначе можно запустить командой “Debug”—“Run” в меню редактора.

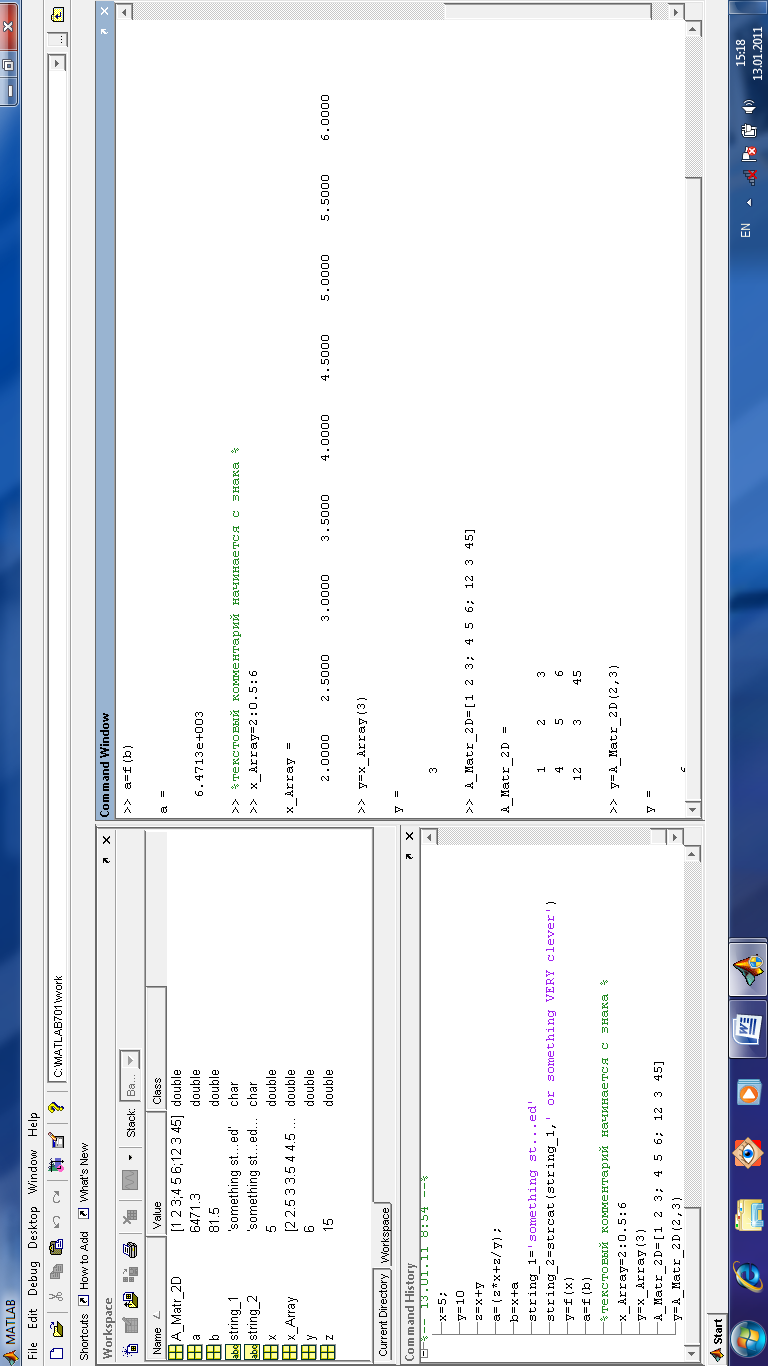
Рис. 1.2. Математические операции.

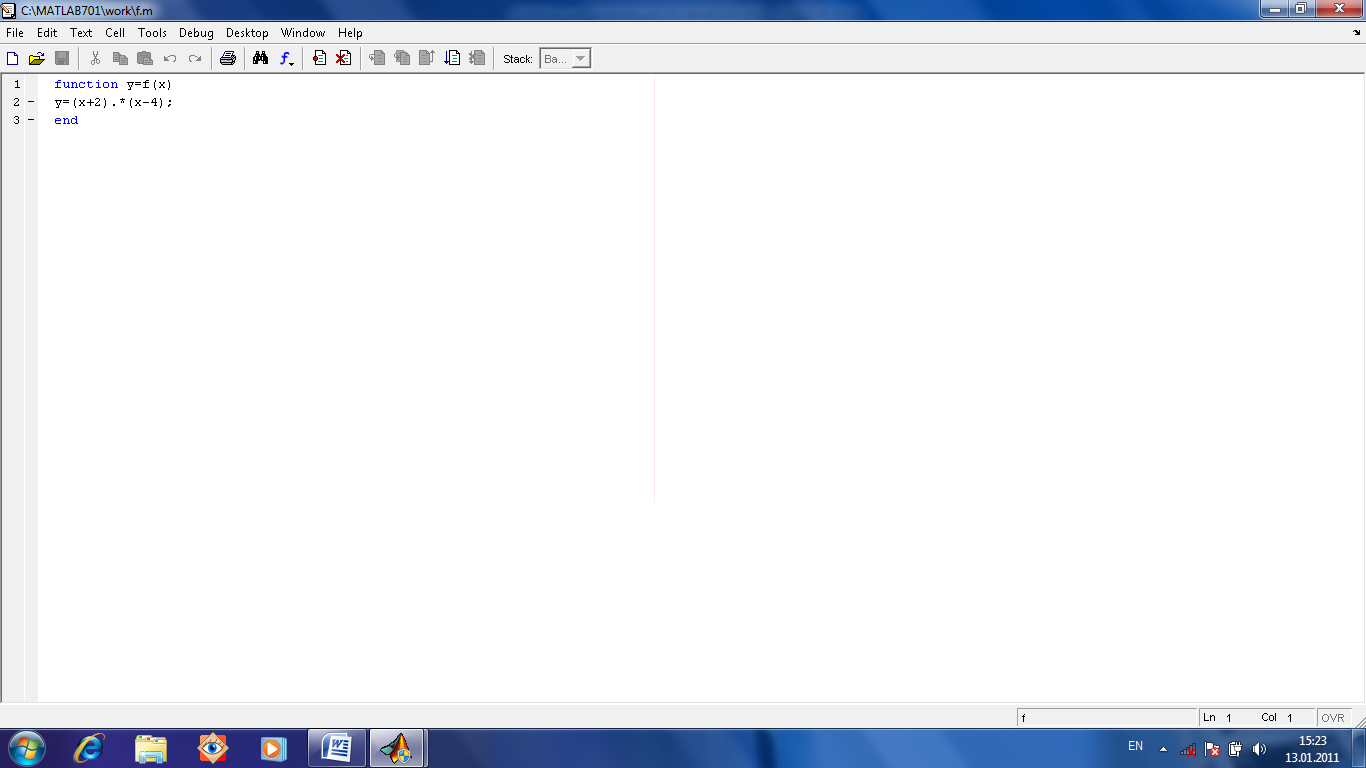
рис. 1.3. описание функции в М-файле

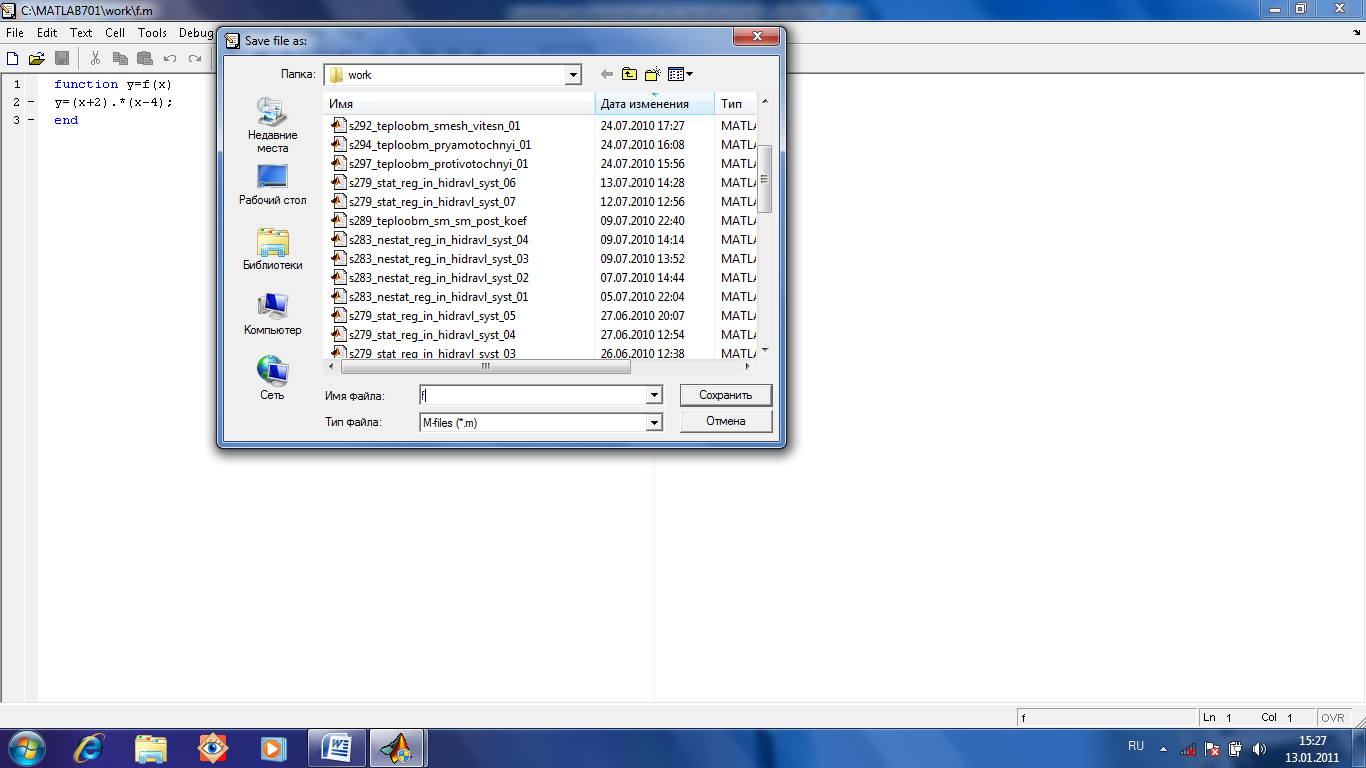
Сохранение File—Save при этом откроется окно в котором надо будет указать где и под каким именем хо тите сохранить этот М-файл. Имя сохраняемого файла должно совпадать с именем описанной в нем функции

Рис. 1.4. Сохранение М-файла

(то есть описанная в нем программа считается функцией и ее описание начинается с указания какого-нибудь имени этой функции, под которым она дальше и будет вызваться для исполнения). (см.рис.1.4.)

Если какие-то М-файлы уже созданы ранее то их можно посмотреть командой File—Open и выбрать тот который нужен.

При написании программы можно писать комментарии начиная их со знака %. (см.рис.1.3).

Function y=f(x)

%функция вычисляется от одного аргумента и возвращает одно

%значение, или от вектора аргумента и возвращает вектор, каждый %элемент которого вычислен от соответствующего элемента вектора %аргумента

y=(x+2).*(x-4); %поэтому перед знаком *умножения стоит .точка .*

%если не ставить ;точку с запятой в конце строки то произойдет вывод на %экран

end

символьная переменная в М-файле:

str=’P I Pupkin’

ее символьное содержимое заключается в кавычки.

Ввод:

xleft=input('введите левую границу интервала поиска ');

Вывод:

disp('ВВОД ИСХОДНЫХ ДАННЫХ края диапазона поиска, точность по аргументу ИЛИ по функции ');

disp(string);

В общем виде обращение к функции

[n1, n2, …, n10]=funName(v1, v2, …, v4)

Где в квадратных скобках необязательный список возвращаемых значений (то есть имена переменных которым будут присвоены соответствующие значения). Если их не указывать то МАТЛАБ сам создаст какие-то переменные и присвоит им эти значения.

В круглых скобках обязательный список аргументов (то есть имена переменных значения которых будут обрабатываться как аргументы функции).

В М-файле описание функции начинается с слова function как в примере

function [x,y,xleft1,xright1,nn]=ZolS1()

в примере функция не нуждается в аргументах поэтому ее список аргументов пуст. Присутствуют только пустые круглые скобки.

Ее вызов в тексте М-файла (в том месте программы где функция вызвана она исполняется)

[x,y,xleft1,xright1,nn]=ZolS1();

Построение графиков

% подготовка к построению графика

h=0.1;

x1=xleft:h:xright; % создан массив точек для графика

y1=f(x1); % создан массив точек для графика

plot(x1,y1,’k-‘);

grid on; % покрыт сеткой

title('y=(x+2)(x-4)'); % подпись наверху

xlabel('X'); % подпись к оси

ylabel('Y');

text(x,y,’\leftarrow Minimum’);%подпись Minimum к стрелке влево,

%которая будет указывать на точку с координатами x,y.

zeroMas=x1*0;

hold on; %обеспечивает построение нового графика в том же окне

plot(masx,masy,’r.’); % график построен

legend(‘plot with minimal step’,’plot with your step’,0);

hold on;

plot(x1,zeroMas,’k-‘,zeroMas,y1,’k-‘); % построены оси

результат этих действий смотри ниже на рис.1.5.

В результате обращения к функции plot(x,y) будет создано окно с именем Figure 1 (так обычно по умолчанию) в котором будет построен график функции У от Х если заранее заданы массив Х и соответствующий ему массив значений функции У.

Тип линии указывается в кавычках plot(x1,y1,'k-');

‘k-‘ Черная сплошная линия.

‘r.’ Круглые красные маркеры без линии.

hold on блокирует создание нового окна то есть новый график будет построен поверх старого на тех же координатных осях.

Рис. 1.5. Пример построения графика

Построение поверхности

Обеспечивается следующим текстом программы (см. рис. 1.6)

% подготовка к построению графика

masx=xleft:hx:xright;

masy=yleft:hy:yright;

masz=fz_xy2(masx,masy); построены массивы координат для точек

%графика

mesh(masx,masy,masz); %построена сеточная поверхность

grid on;

title(‘z=-sqrt(256-x.^2-y.^2)’);

xlabel(‘X’);

ylabel(‘Y’);

zlabel(‘Z’);

text(x,y,z,’\leftarrow Minimum’);

legend(‘z(i,j)=-sqrt(256-x(i)*x(i)-y(j)*y(j))’,0);

где команда mesh(masx,masy,masz); строит сеточную поверхность .

Рис. 1.6. Пример построения поверхности

Операции с матрицами.

Пусть даны две матрицы. (Если не даны, зададим их. Пусть

A=[1 2 3; 5 67 89; 34 21 5];

B=[3 4 5; 54 32 12; 6 7 8];

Тогда имеем две матрицы 3х3 элемента).

Транспонировать матрицу можно так

A_transp=A’; где знак ’ обеспечивает транспонирование матрицы А.

Умножение матриц выполняется так

C_res_mult=A*B; где C_res_mult результат умножения матриц.

Обратная матрица находится так

А_obr=A^(-1);

Или так: A_obr=inv(A);

Поэлементное сложение матриц C=A+B;

Определитель D=det(A);

Решение системы линейных уравнений, где А матрица системы, столбец b столбец свободных членов, столбец х столбец неизвестных:

x=linsolve(A,b);