Задания и методические указания

К.В. Подмастерьев,

Е.В. Пахолкин,

В.В. Мишин

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

По выполнению расчетно-графических

И курсовых работ

По метрологическим дисциплинам

Орел 2003

Авторы: заведующий кафедрой ПМиС, доктор технических наук, профессорК.В. Подмастерьев

доцент кафедры ПМиС, кандидат технических наук Е.В. Пахолкин

доцент кафедры ПМиС, кандидат технических наукВ.В. Мишин

Рецензент: доцент кафедры ПМиС,кандидат технических наук, доцент З.П. Лисовская

Методические указания по выполнению расчетно-графических и курсовых работ по метрологическим дисциплинам содержат задания по обра­ботке экспериментальных данных при выполнении однократных и многократных измерений, нескольких серий измерений, при функцио­нальных преобразованиях результатов измерений и исследовании фи­зических зависимостей.

В настоящих методических указаниях представлены индивидуаль­ные задания пяти видов (по 100 вариантов).

Редактор Т.Д Васильева

Технический редактор <инициалы, фамилия>

Подписано к печати <дата>. Формат 60x84 1/16.

Печать офсетная. Уч.-изд.л. 2,3. Усл. печ. л. _____.. Тираж 100 экз.

Заказ № <число>

Отпечатано с готового оригинал-макета на полиграфической базе ОрелГТУ,

302020, г. Орел, ул. Московская, 65.

Ó ОрелГТУ, 2003

Ó Подмастерьев К.В.,

Пахолкин Е.В.,

Мишин В.В., 2003

Содержание

1 Общие положения
1.1 Содержание расчетно-графической работы
1.2 Оформление работы
2 Задания и методические указания
2.1 Задание 1. Однократное измерение
2.1.1 Условие задания
2.1.2 Указания по выполнению
2.1.3 Порядок расчета
2.2 Задание 2. Многократное измерение
2.2.1 Условие задания
2.2.2 Указания по выполнению
2.2.3 Порядок расчета
2.3 Задание3. Обработка результатов нескольких серий измерений
2.3.1 Условие задания
2.3.2 Указания по выполнению
2.3.3 Порядок расчета
2.4 Задание 4. Функциональные преобразования результатов измерений (косвенные измерения)
2.4.1 Условие задания
2.4.2 Указания по выполнению
2.4.3 Порядок расчета
2.5 Задание 5. Обработка экспериментальных данных при изучении зависимостей
2.5.1 Условие задания
2.5.2 Указания по выполнению
2.5.3 Порядок расчета
Список использованных источников
Приложение А
Приложение Б
Приложение В
Приложение Г
Приложение Д
Приложение Е
Приложение Ж
Приложение И

ОБЩИЕ ПОЛОЖЕНИЯ

Содержание расчетно-графической работы

Согласно государственным образовательным стандартам циклы общепрофессиональных дисциплин практически по любой специальности включают одну из метрологических дисциплин. Напри­мер, по специальности 190100 изучается дисциплина «Метрология, стандартизация, сертификация», по специальностям 220500 и 200800 – «Метрология, стандартизация и технические измерения». При этом рабочие планы для различных специальностей предполагают выполнение расчетно-графических или курсовых работ. Наряду со специфическими задачами изучения метрологической дисциплины для каждой специальности есть общие цели и задачи для всех специальностей.

Одной из основных задач изучения метрологических дисциплин в вузе является освоение методов получения достоверной измеритель­ной информации и правильного ее использования, а также приобрете­ние практических навыков обработки данных при выполнении различных видов измерений.

Решению указанной задачи и служат задания, изложенные в данных методических указаниях. При выполнении работы студент углубляет те­оретические знания и получает практические навыки в области обра­ботки экспериментальных данных при выполнении однократных и многократных измерений, нескольких серий измерений, при функцио­нальных преобразованиях результатов измерений и исследовании фи­зических зависимостей.

В настоящих методических указаниях представлены индивидуаль­ные задания пяти видов (по сто вариантов):

– задание 1. Однократное измерение;

– задание 2. Многократное измерение;

– задание 3. Обработка результатов нескольких серий измерений;

– задание 4. Функциональные преобразования результатов измере­ний;

– задание 5. Обработка экспериментальных данных при изучении зависимостей.

В зависимости от изучаемой дисциплины и планируемого объема работа может включать лишь некоторые из представленных пяти зада­ний.

Оформление работы

Расчетно-графические и курсовые работы оформляются на листах стандарт­ного формата А4 (297x210 мм). Форма титульного листа представлена в приложении А.

Работа должна включать по каждому заданию: условие задачи; экспериментальные данные; априорную информацию; выбранный алго­ритм обработки с соответствующими пояснениями и промежуточные ре­зультаты обработки экспериментальных данных; полученный результат измерений; необходимые графики и диаграммы, поясняющие решение задач.

В конце работы необходимо представить список использованных источников.

ЗАДАНИЯ И МЕТОДИЧЕСКИЕ УКАЗАНИЯ

Задание 1. Однократное измерение

2.1.1 Условие задания

При однократном измерении физической величины получено показание средства измерения X = 10. Определить, чему равно значение измеряемой величины, если экспериментатор обладает априорной информацией о средстве измерений и условиях выполнения измерений согласно данным таблицы 1.

Указания по выполнению

1. Исходные данные студент выбирает из таблицы 1 по предпоследней и последней цифрам шифра; например шиф­ру 96836 соответствует априорная информация, определяемая на пе­ресечении строки 3 столбца 6.

2. Априорная информация в таблице 1 представлена в двух вари­антах. В первом варианте даются сведения о классе точности средс­тва измерений: пределы измерений, класс точности, значение адди­тивной (q_а) или мультипликативной (q_м) поправки. Например, данные: -50...50; 1,5; q_а = 0,5, – означают, что средство измерения имеет диапазон измерений от -50 до 50, класс точности 1,5, а значение аддитивной поправки равняется 0,5.

Во втором варианте в качестве априорной информации даются сведения о видах и характеристиках распределения вероятности ре­зультата измерения: вид закона распределения, значение оценки среднего квадратического отклонения (S_x), доверительная вероятность Р (для нормального закона распределения) и значение адди­тивной (q_а) или мультипликативной (q_м) поправки. Например, данные: норм.; S_x =0,5; Р = 0,95; q_м = 1,1 – означают, что закон расп­ределения вероятности результата измерения нормальный, со значени­ем оценки среднеквадратического отклонения 0,5. При этом имеет место мультипликативная поправка (поправочный множитель) 1,1, а доверительный интервал следует рассчитывать с доверительной веро­ятностью 0,95.

Порядок расчета

Результат измерения при однократном измерении определяется по алгоритму, представленному на рисунке 34 в источнике [1].

Обработка экспериментальных данных зависит от вида используе­мой априорной информации. Если это информация о классе точности, то пределы, в которых находится значение измеряемой ве­личины без учета поправки, определяются следующим образом:

Q₁ = X – DХ; Q₂ = X + DХ,

где DХ - предел допускаемой абсолю­тной погрешности средства измерения при его показании X. Значе­ние DХ определяется в зависимости от класса точности и способа его задания по ГОСТ 8.401-80.

Если в качестве априорной используется информация о законе распределения вероятности, то пределы определяются через дове­рительный интервал:

Q₁ = X – E; Q₂ = X + Е.

Значение Е определяется в зависимости от вида закона распределе­ния вероятности результата измерения. Для нормального закона

Е = t∙S_x,

где t для заданной доверительной вероятности Р выбира­ется из таблиц интегральной функции нормированного нормального распределения Ф(t) (например, табл. 1.1.2.6.2 [2], при этом следует учитывать, что Р = 2Ф(t)). Таблица распределения также приведена в приложении Б.

Для равномерного закона распреде­ления вероятности результата измерения значение Е (аналог довери­тельного интервала) можно определить из выражения

Е = a∙S_x,

где .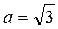

При представлении результата измерения необходимо внести поправки и уточнить пределы, в которых находится значение измеряемой величины.

При вычислении следует руководствоваться прави­лами округления, согласно которым значения среднеквадратических отклонений указываются в окончательном ответе двумя значащими цифрами, если первая из них равна 1 или 2, и одной, если первая равна 3 или более. Все предварительные расчеты выполняются не ме­нее чем с одним или двумя лишними знаками.

В качестве справочных данных могут исполь­зоваться аналогичные таблицы из других литературных источников.

Таблица 1 – Исходные данные
Предпоследняя цифра щифра	Последняя цифра шифра
	0…100 1,0 Qa = 1	-50…+50 0,02/0,01 Qa = -2	0…50 1,0 Qм = 1.1	0…50 4,0 Qм = 0.9	-30…+30 1,5 Qм = 1.2	0…50 0,2/0,1 Qа = -0.5	0…100 4,0 Qа = 0	-50…+50 2,5 Qа = 0	0…30 6,0 Qа = 1	-10…+10 1,0 Qм = 1,1
	норм. Sx = 0,1 P = 0,9 Qa = 1	норм. Sx = 0,5 P = 0,95 Qa = 1,3	норм. Sx = 1 P = 0,9 Qa = -1	норм. Sx = 0,6 P = 0,98 Qa = 0,5	норм. Sx = 0,3 P = 0,9 Qa = 0	норм. Sx = 0,1   Qa = -1,0	норм. Sx = 0,3 Qa = 1,1	норм. Sx = 0,5 P = 0,8 Qa = 0	норм. Sx = 0,6 Qa = 1,0	норм. Sx = 0,2 P = 0,8 Qa = -0,8
	-30…+50 2,5 Qa = 1	-50…+30 2,5 Qa = 1	0…150 1,0 Qм = 1,1	-20…+20 1,5 Qм = 0,9	0…50 2,5 Qa = 0	-10…+20 4,0 Qa = 0,1	0…30 4,0 Qм = 1,2	0…50 0,03/0,01 Qa = 0	0…10 0,02/0,01 Qa = 1,0	0…30 1,0 Qa = 1,1
	норм. Sx = 0,2 P = 0,99 Qa = 0	норм. Sx = 0,3 P = 0,8 Qм = 1,0	норм. Sx = 0,4 P = 0,95 Qa = 0,8	равн. Sx = 0,4 Qa = 1,0	равн. Sx = 0,8 Qм = 0,9	равн. Sx = 0,6 Qa = 1,0	норм. Sx = 0,6 P = 0,8 Qa = 0,5	норм. Sx = 0,7 P = 0,9 Qa = -0,5	равн. Sx = 0,5 Qa = 0,6	равн. Sx = 0,6 Qм = 1,2
	0…100 6,0 Qa = 1,0	-50…+50 1,5 Qм = 0,9	0…30 4,0 Qa = -1,0	-20…+20 1,0 Qa = 0	-30…+30 0,04/0,02 Qa = 1,0	0…50 4,0 Qa = 0,5	-100…100 0,1 Qa = 0,2	1…100 0,2 Qa = 0	0…30 0,5 Qa = 0,9	0…50 0,25 Qa = 0,1
	0…100 4,0 Qa = -0,5	0…50 0,4 Qa = -0,2	-10…+10 0,5 Qa = -1,0	-30…+50 0,25 Qм = 0,9	-100…100 0,1 Qa = 0,5	0…10 1,0 Qa = 0,2	0…50 0,1/0,2 Qм = 1,1	0…100 0,2/0,1 Qм = 1,1	0…50 6,0 Qa = 0,5	-20…+20 0,3/0,2 Q = 0
	норм. Sx = 0,5 P = 0,9 Qa = 0,3	норм. Sx = 0,2 P = 0,95 Qм = 1,1	норм. Sx = 0,4 P = 0,9 Qм = 1,1	норм. Sx = 0,6 P = 0,8 Qa = -1,0	равн. Sx = 0,1   Qa = 0,3	равн. Sx = 0,2   Qa = -0,1	равн. Sx = 0,4   Qм = 0,8	равн. Sx = 0,3 Qa = -0,5	норм. Sx = 0,1 P = 0,9 Qм = 0,95	норм. Sx = 0,4 P = 0,95 Qa = -0,1
	0…15 0,02/0,01 Qa = 1,1	0…20 0,1 Qм= 1,01	-20…+30 0,25 Qa = -0,1	-30…+20 0,25 Qa = -0,1	0…80 0,05 Qa = -0,1	0…100 0,1 Qм= 0,9	0…50 6,0 Qм= 1,2	-10…20 4,0 Qм= 0,9	-20…+20 1,0 Qм= 1,0	-25…+25 1,5 Qa = -0,5
	0…50 0,02/0,01 Qм = 1,1	0…10 0,1 Qa = 0,1	-10…20 0,25 Qм = 0,9	-50…+50 1,5 Qa = 0,1	0…50 1,6 Qм = 0,01	0…20 1,5 Qм = 1	0…50 2,0 Qa = 1	-10…+10 0,01/0,02 Qм = 1,1	0…15 0,5 Qa = 0,1	0…10 0,1 Qa = 0,2
	норм. Sx = 0,5 P = 0,9 Qa = 0,1	норм. Sx = 0,9 P = 0,9 Qa = 0,9	норм. Sx = 1,5 P = 0,8 Qм = 1,1	норм. Sx = 0,9 P = 0,8 Qa = 0	равн. Sx = 0,5 Qa = 1,0	равн. Sx = 0,8 Qa = 0,8	норм. Sx = 0,85 P = 0,95 Qa = 0,1	норм. Sx = 0,9 P = 0,99 Qa = 0	норм. Sx = 0,1 P = 0,95 Qм = 1,1	норм. Sx = 0,2 P = 0,9 Qa = 0,2

Задание 2. Многократное измерение

2.2.1 Условие задания

При многократном измерении одной и той жефизической величины получена серия из 24 результатов измерений Q_i; i Î [1...24]. Эти результаты после внесения поправок представлены в таблице 2. Определить результат измерения.

Таблица 2 – Исходные данные

Предпоследняя цифра шифра	Последняя цифра шифра
											482 495
											492 484
											483 494
											492 486
											481 494
											495 484
											485 492
											492 483
											482 493
											493 480

Указания по выполнению

1. Серию экспериментальных данных студент выбирает из таблицы 2 по предпоследней и последней цифрам шифра. Например, шифру 96836 соответствует серия, включающая все результаты измерений, которые приведены в строке 3 и столбце 6.

2. Результат измерения следует получить с доверительной вероятностью 0,95.

Порядок расчета

Результат многократного измерения находится по алгоритму, представленному на рисунке 40 [1]. При этом необходимо учитывать, что n = 24, следовательно, порядок расчетов и их содержание определяются условием 10…15 < n < 40…50.

1. Определить точечные оценки результата измерения: среднего арифметического 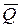и среднего квадратического отклонения S_Q результата измерения.

2. Обнаружить и исключить ошибки. Для этого необходимо:

– вычислить наибольшее по абсолютному значению нормированное отклонение

;

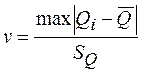– задаться доверительной вероятностью Р и из соответствующих таблиц (таблица П.6 [3] или из таблица В.1) с учетом q = 1 – Р найти соответствующее ей теоретическое (табличное) значение ν_q;

– сравнить ν с ν_q.

Если ν > ν_q, то данный результат измерения Q_i является оши­бочным, он должен быть отброшен. После этого необходимо повторить вычисления по пунктам 1 и 2 для сокращенной серии результатов изме­рений. Вычисления проводятся до тех пор, пока не будет выполнять­ся условие ν < ν_q.

3. Проверить гипотезу о нормальности распределения оставших­ся результатов измерений.

Проверка выполняется по составному критерию [3].

Применив критерий 1, следует:

– вычислить отношение

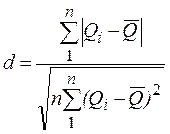
– задаться доверительной вероятностью P₁ (рекомендуется принять P₁ = 0,98) и для уровня значимости q₁ = 1 – Р₁ по соответствующим таблицам (таблица П.7 [3] или таблица Г.1) определить квантили рас­пределения d_1-0,5ql ,и d_0,5q1;

– сравнить d с d_1-0,5ql и d_0,5q1.

Если d_1-0,5q1 < d < d_0,5q1, то гипотеза о нормальном законе распределения вероятности результата измерения согласуется с экспериментальными данными.

Применив критерий 2, следует:

– задаться доверительной вероятностью Р₂ (рекомендуется принять Р₂ = 0,98) и для уровня значимости q₂ = 1 – Р₂ с учетом n опреде­лить по соответствующим таблицам (таблица П.8 [3] или таблица Г.2) зна­чения m и Р*;

– для вероятности Р* из таблиц для интегральной функции нормиро­ванного нормального распределения Ф(t) (таблица 1.1.2.6.2 [2] или таблица Б.1) определить значение t и рассчитать Е = t∙S_Q.

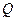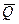Если не более m разностей | _i - | превосходит Е, то гипо­теза о нормальном законе распределения вероятности результата из­мерения согласуется с экспериментальными данными, закон можно признать нормальным с вероятностью Р₀ ³ (Р₁ + Р₂ – 1).

Если хотя бы один из критериев не соблюдается, то гипотезу о нормальности распределения отвергают.

4. Определить стандартное отклонение среднего арифметическо­го.

Если закон распределения вероятности результата измерений признан нормальным, то стандартное отклонение определяют как .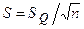

Если гипотеза о нормальности распределения отвергает­ся, то

.

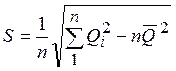5. Определить доверительный интервал.

Если закон распределения вероятности результата измерений признан нормальным, то доверительный интервал для заданной дове­рительной вероятности Р определяется из распределения Стьюдента Е = t×S, где t выбирается из соответствующих таблиц (таблица 1.1.2.8 [2] или таблица Д.1, при этом m = n – 1, а a = Р).

Если гипотеза о нормальности распределения отвергается, то t определяется из неравенства П. Л. Чебышева:

Р ³ 1 – 1/t².

Задание3. Обработка результатов нескольких серий измерений

2.3.1 Условие задания

При многократных измерениях одной и той же величины получены две серии по 12 (n_j) результатов измерений в каждой. Эти результаты после внесения поправок представлены в таблице 2. Вычислить результат многократных измерений.

Указания по выполнению

1. Серии в таблице 2 студент выбирает по предпоследней и пос­ледней цифрам шифра: например, шифру 96836 соответствуют все ре­зультаты измерений, которые приведены в строке 3 (серия 1) и столбце 6 (серия 2).

2. Результат измерения следует получить с достоверностью 0,95.

Порядок расчета

Обработку результатов двух серий измерений целесообразно осуществлять по алгоритмам [1, с. 122-129] (последовательность расчетов и их содержание определяются условием 10...15 < n < 40...50).

1. Обработать экспериментальные данные в каждой j-й серии отдельно по алгоритму, изложенному в задании 2 (алгоритм обработки многократных измерений), при этом:

– определить оценки результата измерения Q_j и среднего квадратического отклонения s_qj;

– обнаружить и исключить ошибки;

– проверить гипотезу о нормальности распределения оставшихся ре­зультатов измерений.

2. Проверить значимость различия средних арифметических се­рий по алгоритму, представленному на рисунке 48 [1]. Для этого следует:

– вычислить моменты закона распределения разности:

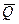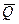G = ₁ - ₂,

;

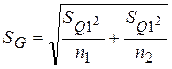– задавшись доверительной вероятностью Р, определить из соответс­твующих таблиц интегральной функции нормированного нормального распределения Ф(t) (таблица 1.1.2.6.2 [2] или таблица Б.1) значение t;

– сравнить |G| с t × S_g.

Если |G| 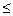t · S_g, то различие между средними арифметическими в сериях с доверительной вероятностью Р можно признать незначимым.

3. Проверить равнорассеянность результатов измерений в сери­ях по алгоритму, изложенному на рисунке 50 [1]. Для этого необходимо:

– определить значение ;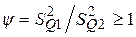

– задавшись доверительной вероятностью Р, определить из соответ­ствующих таблиц (таблица 16 [1] или таблица Е.1) значение аргумента ин­тегральной функции распределения вероятности Фишера y₀;

– сравнить y с y₀.

Если y < y₀, то серии с доверительной вероятностью Р счи­тают рассеянными.

4. Обработать совместно результаты измерения обеих серий с учетом того, однородны серии или нет.

Если серии однородны (равнорассеянны с незначимым различием средних арифметических), то все результаты измерения следует объ­единить в единый массив и выполнить обработку по алгоритму на рисунке 40 [1]. Для этого необходимо:

– определить оценку результата измерения 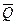и среднего квадратического отклонения S:

;

;

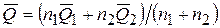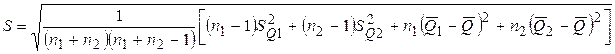– задавшись доверительной вероятностью Р, определить из таблиц распределения Стьюдента (таблица 1.1.2.8 [2] или таблица Д.1) значение t для числа степеней свободы ;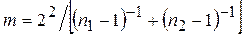

– определить доверительный интервал Е = t×S.

Если серии не равнорассеянны с незначимым различием средних арифметических, то совместную обработку результатов измерений следует выполнять с учетом весовых коэффициентов по алгоритму, представленному на рисунке 51 [1].

Для этого необходимо:

– определить оценки результата измерения – 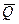и среднего квадратического отклонения S:

;

;

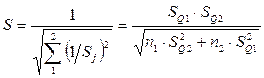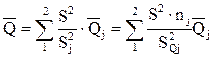– аналогично предыдущему случаю, задавшись доверительной вероят­ностью Р, определить t и доверительный интервал.

Если различие средних арифметических в сериях признано зна­чимым, то результаты измерений в каждой серии следует обработать раздельно по алгоритму многократных измерений:

– в зависимости от закона распределения вероятности результата измерения в каждой серии определить S_j;

– задавшись доверительной вероятностью Р, определить по соответ­ствующим таблицам значение t_j;

– рассчитать доверительный интервал Е_j =S_j × t_j.

Задание 4. Функциональные преобразования результатов