Основные законы и соотношения для магнитных цепей

2.1. Закон полного тока

Магнитное поле создается электрическими токами. Закон полного тока устанавливает связь между напряженностью магнитного поля и током, возбуждающим это поле. Способность тока возбуждать магнитное поле определяется намагничивающей (магнитодвижущей) силой F. Под намагничивающей силой катушки с током понимают произведение числа витков катушки 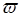на протекающий по ней ток I ( 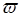I – ампервитки). Положительное направление намагничивающей силы совпадает с направлением движения острия буравчика, если его вращать по направлению тока в обмотке (рис.33.2).

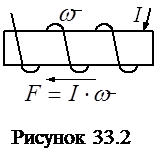Закон полного тока формулируется следующим образом:

Интеграл от напряженности магнитного поля по любому замкнутому контуру равен алгебраической сумме токов (полному току), сцепленных с этим контуром

,

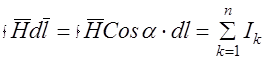(33.1)

где Н – вектор напряженности поля в данной точке пространства;

dl – элемент длины замкнутого контура;

α – угол между 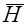и ;

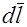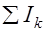– сумма токов, пронизывающих контур.

Ток I_k берется в сумме со знаком плюс, если направление обхода контура и направление тока связаны правилом буравчика. Например, для рисунка 33.3

.

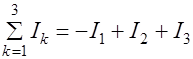Если направления векторов 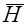и 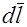совпадают, а намагничивающая сила создается катушкой с током I и

.

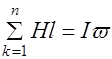(33.2)

числом витков 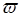, то для такой цепи

Таким образом, согласно закону полного тока, намагничивающая сила равна сумме произведений напряженности поля на длину соответствующих участков магнитной цепи. Величину Hl называют магнитным напряжением и измеряют в амперах.

2.2. Вебер-амперные характеристики

Под вебер-амперной характеристикой понимают зависимость магнитного потока по какому-либо участку магнитной цепи от падения магнитного напряжения на этом участке: 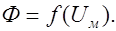Она также важна при расчетах магнитных цепей, как и ВАХ нелинейных резисторов при расчетах нелинейных электрических цепей.

Вебер-амперные характеристики при расчетах магнитных цепей не задаются. Перед расчетом их необходимо построить, используя кривые намагничивания ферромагнитных материалов, входящих в магнитную цепь.

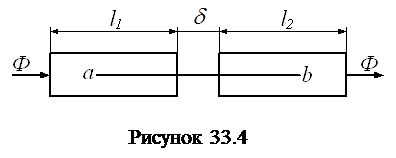Пусть на участке магнитной цепи, изображенном на рисунке 33.4, проходит магнитный поток Ф. Участки l₁ и l₂ сечением S выполнены из ферромагнитного материала, для которого задана основная кривая намагничивания, а δ – воздушный зазор. Требуется построить вебер-амперную характеристику участка цепи между точками a и b.

При построении сделаем следующие допущения:

1) магнитный поток вдоль всего участка от a до b постоянен (рассеяние отсутствует);

2) сечение магнитного потока в воздушном зазоре такое же, как и на участках l₁ и l₂.

В действительности эти допущения справедливы лишь при относительно небольших воздушных зазорах. Построение вебер-амперной производим следующим образом:

1. Задаемся значениями магнитной индукции в пределах основной кривой намагничивания;

2. По кривой намагничивания находим соответствующие значения напряженности поля;

3. вычисляем напряженность поля в воздушном зазоре:

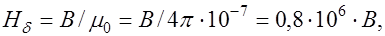
где H – в А/м; В – в Тл; μ₀ – в Гн/м.

4. Для каждого значения магнитной индукции вычисляем магнитный поток 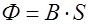и магнитное напряжение:

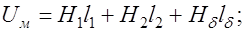
5. По результатам расчета строим зависимость 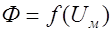(рис.33.5).

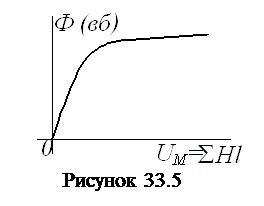
2.3 Законы Кирхгофа для магнитной цепи

Магнитные цепи, как и электрические, подразделяют на неразветвленные и разветвленные. Как и в электрических цепях, в магнитных имеются ветви и узлы.

Первый закон Кирхгофа для магнитных цепей формулируется следующим образом:

Алгебраическая сумма магнитных потоков в любом узле магнитной цепи равна нулю:

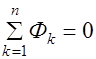(33.3)

Второй закон Кирхгофа относится к контурам магнитной цепи и формулируется следующим образом:

Алгебраическая сумма магнитных падений напряжений вдоль любого замкнутого контура магнитной цепи равна алгебраической сумме магнитодвижущих сил вдоль того же контура:

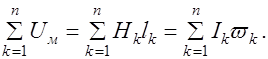(33.4)

При записи уравнений по законам Кирхгофа произвольно выбирается положительное направление магнитных потоков и направление обхода контура. Если направление магнитного потока или магнитодвижущей силы совпадает с направлением обхода контура, то соответствующие слагаемые входят в уравнения со знаком плюс.

2.3. Закон Ома для магнитной цепи

По определению, падение магнитного напряжения 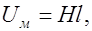но

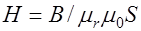, где S – сечение участка магнитной цепи.

Следовательно 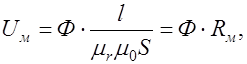где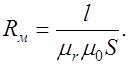

Уравнение

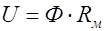(33.5)

называют законом Ома для магнитной цепи. В этом уравнении R_м – магнитное сопротивление участка магнитной цепи. Величину, обратную магнитному сопротивлению, называют (1/R_м = G_м) магнитной проводимостью участка магнитной цепи.

Вопросы для самоконтроля

1. Чем обусловлено явление ферромагнетизма?

2. Почему при определенной напряженности магнитного поля наблюдается насыщение ферромагнитного материала?

3. Чем обусловлен магнитный гистерезис?

4. Что понимают под остаточной магнитной индукцией ферромагнитного материала?

5. Какую характеристику ферромагнитного материала называют коэрцитивной силой? Что она характеризует?

6. Какие ферромагнитные материалы называют магнитомягкими и почему? Где применяют магнитомягкие материалы?

7. Какие ферромагнитные материалы называют магнитотвердыми и почему? Где применяют магнитотвердые материалы?

8. Сформулируйте закон полного тока в интегральной форме и прокомментируйте его.

9. Какую величину понимают под намагничивающей силой (магнитодвижущей силой) катушки с током?

10. Что понимают под магнитным падением напряжения? В каких единицах измеряется магнитное напряжение?

11. Какую характеристику магнитной цепи называют вебер-амперной? Поясните порядок построения вебер-амперной характеристики для участка магнитной цепи.

12. Сформулируйте законы Кирхгофа для магнитной цепи.

13. Проделайте вывод закона Ома для участка магнитной цепи.