Проекція сили на вісь – це взята з відповідним знаком величина, яка
ГРАФІЧНА РОБОТА №2
Тема:Плоска система довільно розташованих сил
Мета:Набути практичних навичок застосування умов рівноваги
плоскої системи довільно розташованих сил для визначення
реакцій в опорах двохопорної балки
Завдання:Визначити реакції в опорах двохопорної балки, навантаженої
зосередженою силою F, рівномірно-розподіленим
навантаженням q та парою сил з моментом М.
| 2 4 4м |
| F М q |
| α |
Таблиця 2 – Вихідні дані
| Варіант | F, кН | q, кН/м | М, кНм |
| Nсп | 5Nсп | Nсп | 10Nсп |
*Nсп – номер за списком в журналі.
Методичні вказівки щодо виконання
Індивідуальної розрахунково-графічної роботи №2
Алгоритм виконання:
1. Найменувати опори балки
Опори балок іменуються зліва направо заголовними буквами латинського алфавіту (А, В,….)
2. Проставити реакції опор балки
Типи опор та їх реакції:
СТРИЖЕНЬ
Така в’язь здійснюється тонким невагомим стрижнем,
Закріпленим на кінцях шарнірами. При цьому стрижень
| Рисунок 1.1 |
з’єднує його шарнірні кінці. Тому реакція R стрижня (рис.1.2)
направлена вздовж осі стрижня в той чи інший бік.
| RА А |
| В RВ |
Рисунок 1.2 – Реакції в стрижневі опорі
ЦИЛІНДРИЧНИЙ ШАРНІР (ШАРНІРНО-НЕРУХОМА ОПОРА)
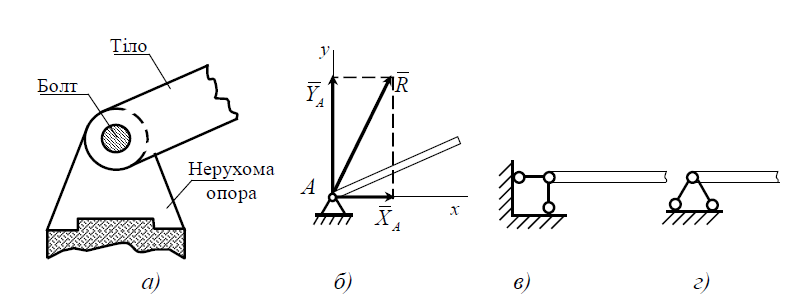
Рисунок 1.3 – Шарнірно-нерухома опора та реакції в ній.
Циліндричний шарнір дозволяє тілу обертатися навколо нерухомої осі та ковзати вздовж неї, але обмежує переміщення тіла в напрямках, перпендикулярних до осі шарніра.
Реакція циліндричного шарніра ( R на рис. 1.3а R на рис. 1.3б) лежить в площині, перпендикулярній осі шарніра, її напрям наперед вказати не можна. Тому реакцію циліндричного шарніра виражають у вигляді двох взаємно перпендикулярних складових (УА та ХА на рис.1.3б).
Рухомий циліндричний шарнір
(ШАРНІРНО-РУХОМА ОПОРА)
У техніці така в’язь реалізується у вигляді опори на котках, якою в точці А закріплена мостова конструкція на рис. 1.4а
У деяких випадках рухомий циліндричний шарнір зображають беззображення котків між опорою та опорною поверхнею, як показано на рис.1.4,б.
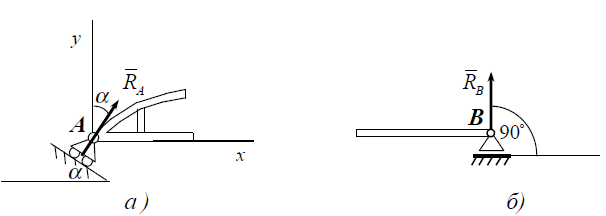
Рисунок 1.4 – Шарнірно-рухома опора
Рухомий циліндричний шарнір обмежує переміщення тіла вздовж нормалі до опорної поверхні, тому його реакція направлена перпендикулярно опорній поверхні, проходячи через центр шарніра
3. Скласти рівняння рівноваги
Для двохопорної балки рівняння рівноваги зручніше подавати у формі:
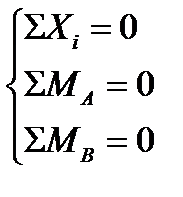
Проекція сили на координатну вісь:
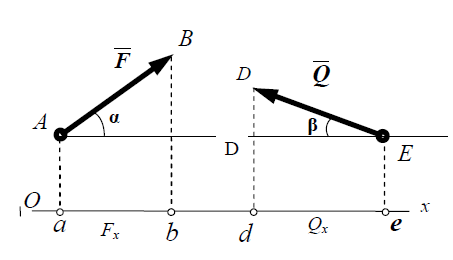
Рисунок 1.5 – Проекції сили на вісь
Проекція сили на вісь – це взята з відповідним знаком величина, яка
чисельно дорівнює відстані між проекціями на цю вісь початку і кінця вектора сили.
При цьому проекція буде додатною, якщо кут між напрямком сили і додатним напрямком осі буде гострим, і від’ємною, якщо цей кут – тупий.
Тоді для сил, зображених на рис. 1.5, одержимо:
Fx = ab = F × cosα,
Qx = ed = -Q × cos β
Якщо сила перпендикулярна до осі, то її проекція на цю вісь дорівнює 0 .
МОМЕНТ СИЛИ
Вище було встановлено, що проекція сили на вісь або площину характеризує здатність сили переміщувати тіло в деякому напрямку. Але дія сили на тіло не обмежується таким зміщувальним ефектом. При певних умовах сила здатна обертати тіло навколо точки або осі. Для врахування обертальної дії сили вводиться поняття моменту сили.
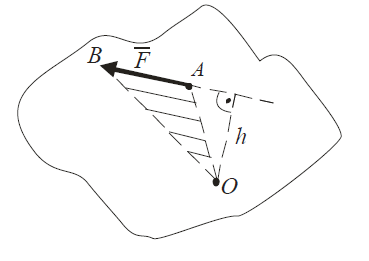
Рисунок 1.6 – Обертова дія сили
Моментом сили відносно точки називають взяту з певним знаком величину, що дорівнює добутку модуля сили на плече (рис. 1.6):
МО (F) = ± F·h.
Знак алгебраїчного моменту вибирають у залежності від напряму повороту тіла під дією сили:
момент сили вважається додатним, якщо сила намагається повернути тіло відносно точки по ходу годинникової стрілки і від’ємним – при повороті проти годинникової стрілки.
Так на рис. 1.6 маємо, що M0 (F )< 0.
4. Визначити реакції опор балки
Після складених рівнянь рівноваги визначаємо невідомі – реакції в опорах балки
5. Скласти рівняння перевірки
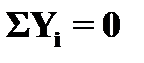
Проекції сили на вісь ОУ (для сил зображених на рис.1.5)
Fу = F × sinα,
Qy = Q × sinβ
6. Зробити висновок щодо отриманих результатів
Якщо умова перевірки виконується, значить реакції знайдено вірно.
Якщо знак реакції « - » - це означає, що в дійсності дана сила спрямована в протилежний бік.
7. Оформити звіт
ПРИКЛАДРОЗВ’ЯЗКУ
| 1 5 4м |
| ХВ х В |
| А |
| F М YВ |
| RА α |
| у |
| q |
Складаємо рівняння рівноваги:
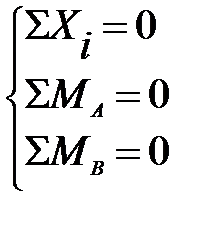
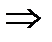
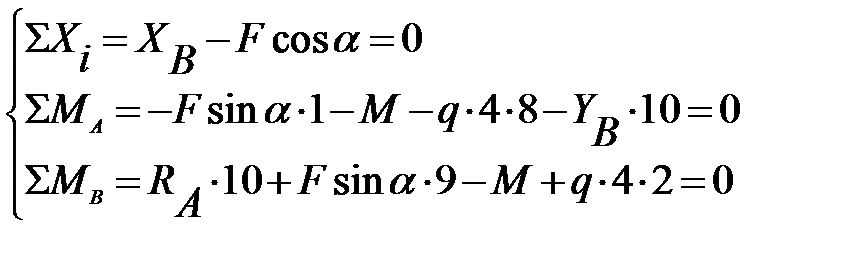
З отриманих рівнянь визначаємо реакції опор:
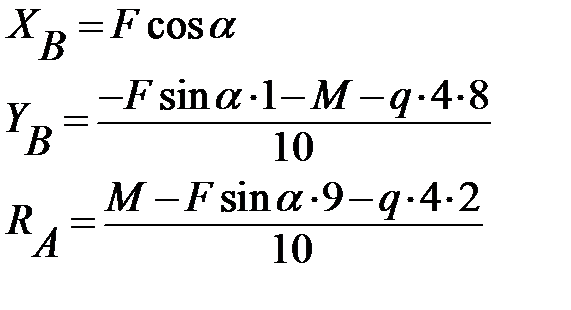
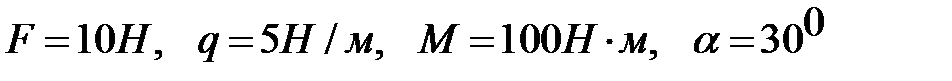При заданих
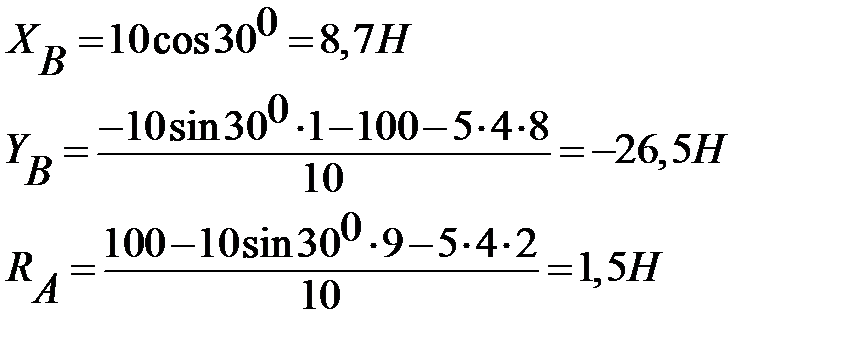
Рівняння перевірки:
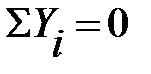
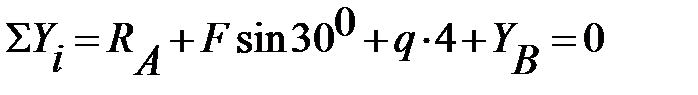
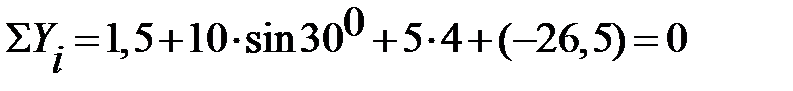
Висновок: Оскільки умова перевірки виконується, значить реакції в опорах
балки знайдені вірно. Знак «-« вказує на те, що складова реакції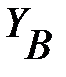 
в дійсності спрямована вниз.