Фазовое пространство системы частиц

Микросостояние системы частиц отображается точкой фазового пространства

,

где и – обобщенные координата и импульс частицы системы; n – число степеней свободы системы. Число n равно числу проекций координат всех частиц и пропорционально числу частиц. Число проекций импульсов равно числу проекций координат, поэтому число независимых координат фазового пространства равно 2n. Для каждой системы используется свое фазовое пространство.

Координата частицы газа и ее импульс с течением времени изменяются согласно уравнениям Гамильтона

, (2.1а)

. (2.1б)

Уильям Гамильтон (1805–1865)

Гамильтониан – полная энергия системы в виде суммы кинетических и потенциальных энергий всех частиц, выраженная через координаты и импульсы частиц:

.

Для нерелятивистской частицы k массой кинетическая энергия

.

Для консервативной системы полная энергия сохраняется

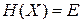
и микросостояния находятся на гиперповерхности фазового пространства.

Уравнения Гамильтона для одномерного движения частицы. Используем гамильтониан

.

Из уравнения Гамильтона (2.1а)

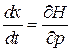
с учетом определения скорости

получаем известное соотношение между импульсом и скоростью

.

Из уравнения Гамильтона (2.1б)

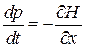
находим

– второй закон Ньютона. Уравнения Гамильтона являются унифицированной формой записи известных уравнений механики на основе гамильтониана.