Рассмотрим систему n линейных алгебраических уравнений с n неизвестными 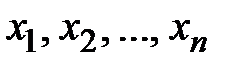 :
:
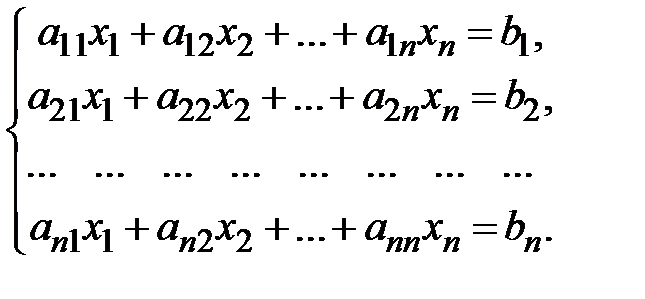
Составим из коэффициентов  при неизвестных определитель
при неизвестных определитель
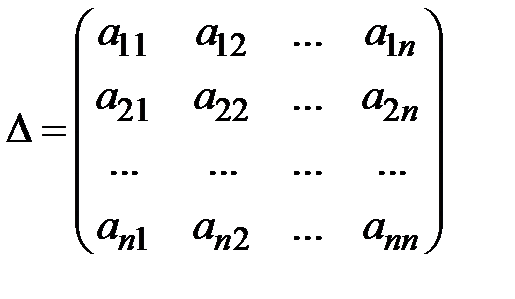
и назовем его определителем системы. Если 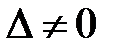 , то система имеет единственное решение
, то система имеет единственное решение
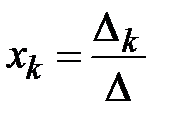 (
( 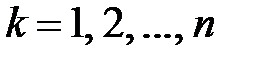 ) (правило Крамера),
) (правило Крамера),
где 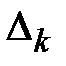 - определитель, получающийся из
- определитель, получающийся из  при замене элементов k-го столбца соответствующими свободными членами
при замене элементов k-го столбца соответствующими свободными членами 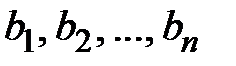 .
.
Если 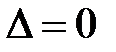 , а среди
, а среди 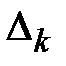 есть не равные нулю, то система не имеетрешения.
есть не равные нулю, то система не имеетрешения.
Пример. Решить методом Крамера систему уравнений
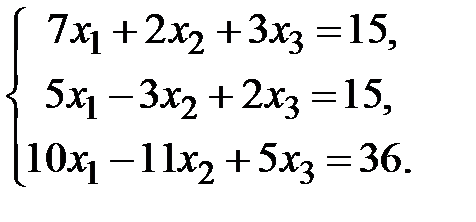
◄ Вычисляем определитель системы: 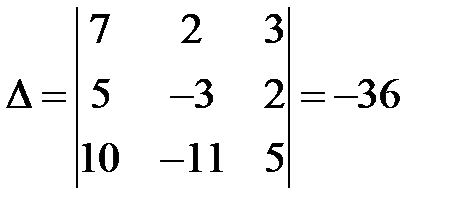 . Система совместна и имеет единственное решение, так как
. Система совместна и имеет единственное решение, так как 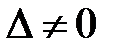 .
.
Вычисляем вспомогательные определители:
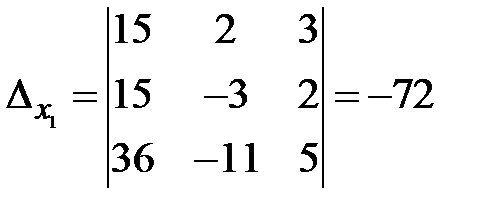 ,
, 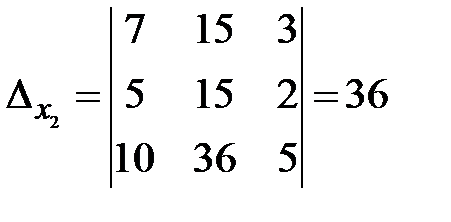 ,
, 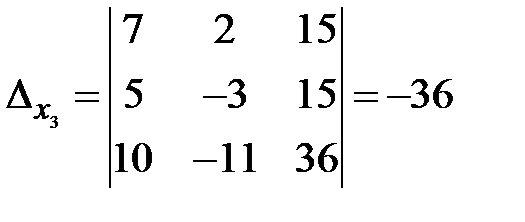 .
.
По формулам Крамера получаем: 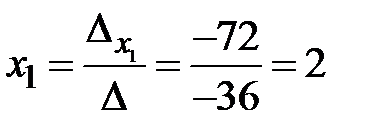 ,
, 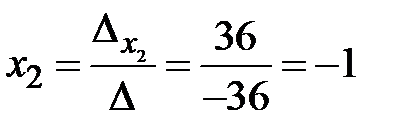 ,
, 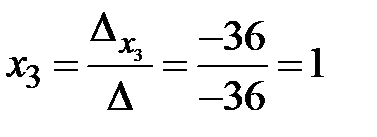 . ►
. ►
Лекция 1.2 «Векторная алгебра»
Учебные вопросы:
1. Векторы. Координаты вектора
2. Линейные операции над векторами
3. Скалярное и векторное произведение векторов
Векторы. Координаты вектора
Векторная величина (вектор) – величина, которая характеризуется не только значением, но и направлением (сила, скорость, ускорение и др.). Скалярная величина (скаляр) – величина, не обладающая направлением (масса, электрический заряд, теплоемкость и др.).
Геометрически вектор представляется направленным отрезком прямой линии (рис. 1). Вектор обозначается как
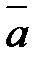
или
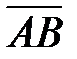
(т.
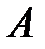
– начало, т.
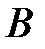
– конец вектора). Длина (модуль, норма, абсолютная величина) вектора обозначается
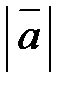
или
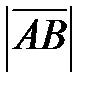
.
Коллинеарные векторы – векторы, лежащие на параллельных прямых (или на одной и той же прямой). На рис. 2 векторы
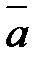
,
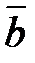
и
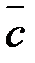
– коллинеарные;
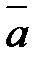
и
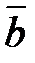
– однонаправлены,
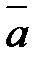
и
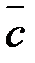
– противоположно направлены.
Компланарными векторами называются векторы, лежащие в параллельных плоскостях. Если компланарные векторы привести (параллельным перемещением) к общему началу, то они будут лежать в одной плоскости.
Нулевой вектор (нуль-вектор)  – вектор, у которого конец и начало совпадают (его модуль
– вектор, у которого конец и начало совпадают (его модуль 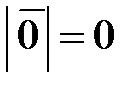 ).
).
Вектор, модуль которого равен 1, называется единичным вектором или ортом.
Два вектора и равны
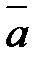 =
= 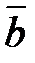 ,
,
если они одинаково направлены и имеют один и тот же модуль ( 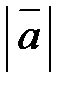 =
= 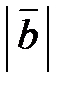 ).
).
Векторы, имеющие равные модули и противоположно направленные, называются противоположными векторами. Вектор, противоположный вектору 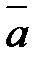 , обозначается через –
, обозначается через – 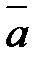 (
( 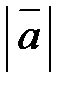 =
= 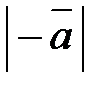 ). Из определения противоположного вектора следует –(–
). Из определения противоположного вектора следует –(– 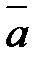 )=
)= 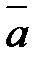 .
.
Ось – прямая, на которой выделено одно из двух ее направлений. Это выделенное направление называется положительным, а противоположное – отрицательным. Ось

можно задать любым вектором, лежащим на ней и имеющим то же направление (рис. 3).
Проекция точки 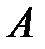 на ось
на ось  есть основание
есть основание
перпендикуляра
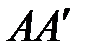
(точка
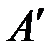
), опущенного из т.
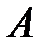
на эту ось (рис. 4).
Компонентой (составляющей) вектора 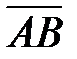 на ось
на ось  называется вектор
называется вектор 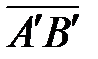 , где
, где 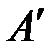 – проекция начала, а
– проекция начала, а 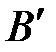 – конца на эту ось (рис. 4.5). Компоненту вектора называют также геометрической проекцией вектора на ось (обозначают
– конца на эту ось (рис. 4.5). Компоненту вектора называют также геометрической проекцией вектора на ось (обозначают 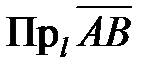 ). Если ось
). Если ось  задана вектором
задана вектором 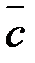 , то вектор
, то вектор 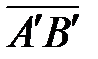 называется также компонентой (геометрической проекцией
называется также компонентой (геометрической проекцией 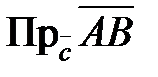 ) вектора
) вектора 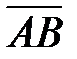 на направление вектора
на направление вектора 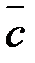 .
.
Алгебраической проекцией (просто проекцией) вектора
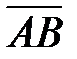
на ось

(или на направление вектора
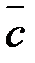
) называется длина вектора
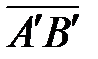
(см. рис. 5), взятая со знаком “+”, если вектор
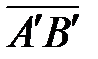
имеет то же направление, что и ось

, или “–“, если ― противоположное направление. Проекция обозначается
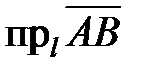
или
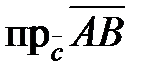
. Для случая, представленного на рис. 5, проекция вектора
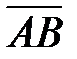
на ось

будет иметь отрицательный знак.
Декартова прямоугольная система координатв пространстве (3-х мерном) представляет собой три взаимно перпендикулярных оси
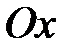
,
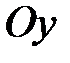
и
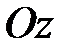
, пересекающихся в начале координат

, при заданной единице масштаба для всех трех осей (рис. 6). Название осей:
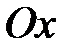
– ось абсцисс,
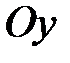
– ось ординат,
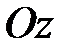
– ось аппликат.
Декартовы координаты точки 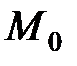 есть расстояния ее проекций
есть расстояния ее проекций 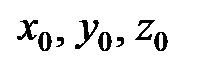 (рис. 6) на координатные оси от начала координат, взятые со знаком “+”, если проекция лежит по отношению к началу в положительном направлении оси, и со знаком “–“, если ― в отрицательном. Обозначение координат точки:
(рис. 6) на координатные оси от начала координат, взятые со знаком “+”, если проекция лежит по отношению к началу в положительном направлении оси, и со знаком “–“, если ― в отрицательном. Обозначение координат точки:  .
.
Единичные векторы (орты)
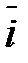
,
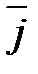
,
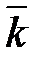
осей
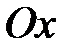
,
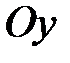
и
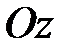
соответственно (рис. 4.7) образуют систему базисных векторов (базис (ортонормированный)). Эти единичные векторы попарно перпендикулярны друг другу и носят название базисных векторов.
Координаты вектора 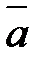 есть его алгебраические проекции на оси координат. Если начало вектора совмещено с началом координат (рис. 7), то координатами вектора будут координаты его конца. Запись координат вектора:
есть его алгебраические проекции на оси координат. Если начало вектора совмещено с началом координат (рис. 7), то координатами вектора будут координаты его конца. Запись координат вектора: 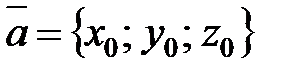 .
.
Если точка
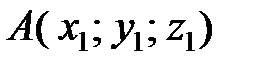
является началом вектора
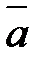
, а точка
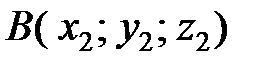
― его концом (рис. 8), то
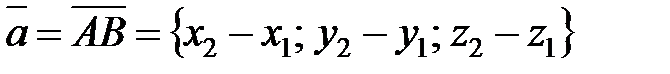 , (1)
, (1)
а его длина (модуль)
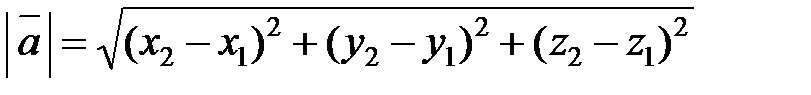 . (2)
. (2)
Направление вектора можно задать углами
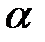
,
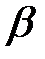
,
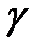
, образуемые положительными направлениями координатных осей
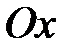
,
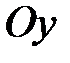
и
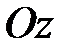
с вектором
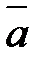
(рис. 9). Косинусы этих углов называются направляющими косинусами вектора:
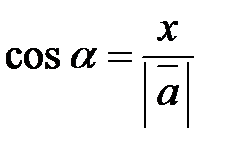 ,
,
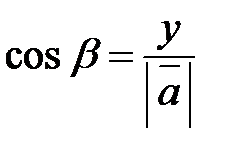 , (3)
, (3)
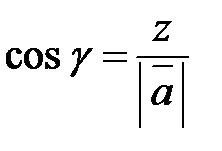 .
.
Для этих косинусов справедливо равенство:
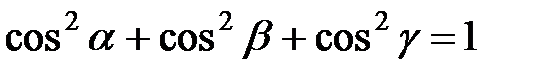 . (4)
. (4)
Пример. Найти длину и направляющие косинусы вектора, проведенного из точки 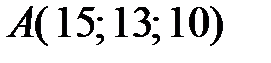 в точку
в точку 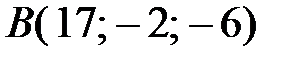 .
.
◄ По формуле (4.1) находим координаты вектора: 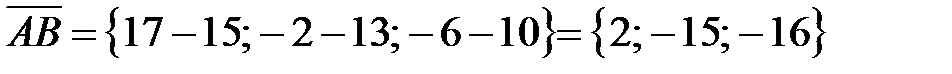 . Согласно (2) длина вектора
. Согласно (2) длина вектора 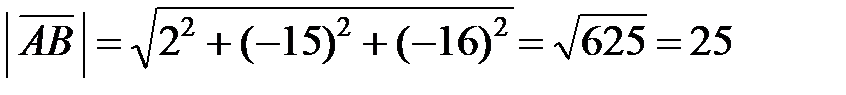 . По формулам (4.3) находим направляющие косинусы:
. По формулам (4.3) находим направляющие косинусы: 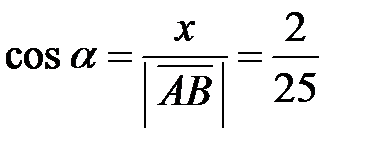 ,
, 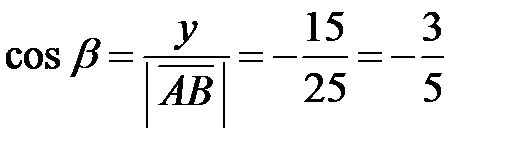 ,
, 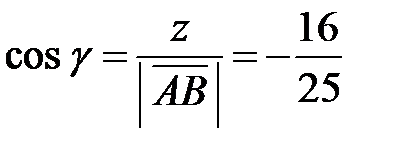 . Проводим проверку на основе равенства (4):
. Проводим проверку на основе равенства (4): 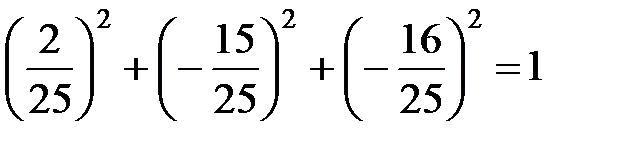 ►
►
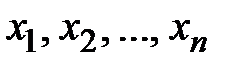 :
: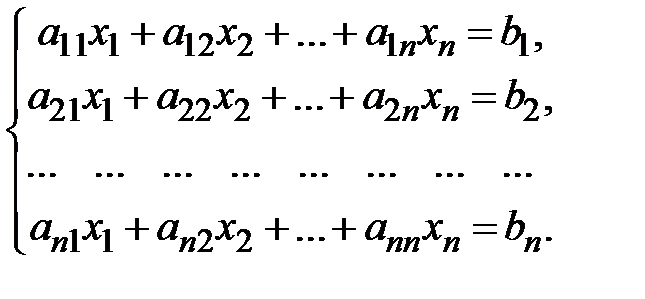
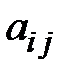 при неизвестных определитель
при неизвестных определитель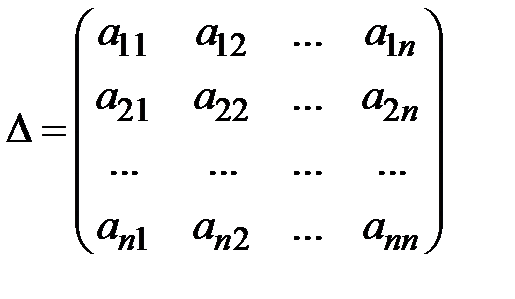
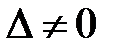 , то система имеет единственное решение
, то система имеет единственное решение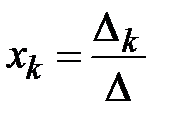 (
( 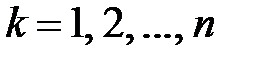 ) (правило Крамера),
) (правило Крамера),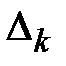 - определитель, получающийся из
- определитель, получающийся из  при замене элементов k-го столбца соответствующими свободными членами
при замене элементов k-го столбца соответствующими свободными членами 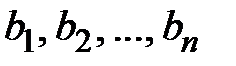 .
.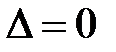 , а среди
, а среди 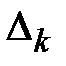 есть не равные нулю, то система не имеетрешения.
есть не равные нулю, то система не имеетрешения.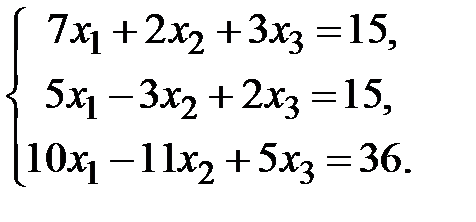
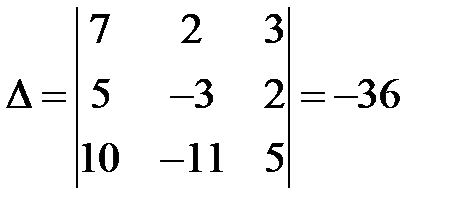 . Система совместна и имеет единственное решение, так как
. Система совместна и имеет единственное решение, так как  .
.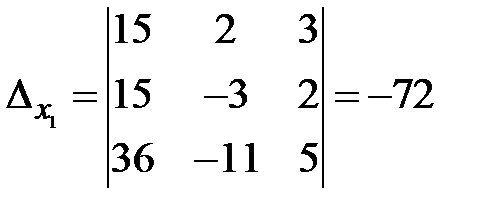 ,
, 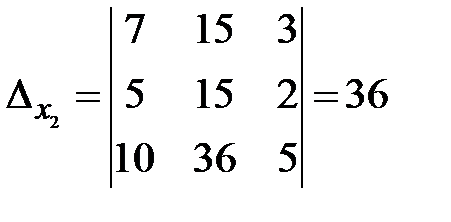 ,
, 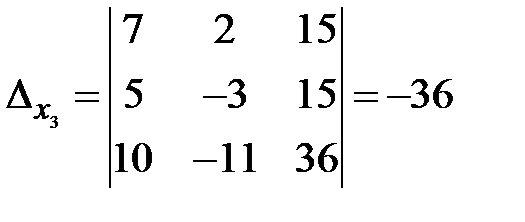 .
.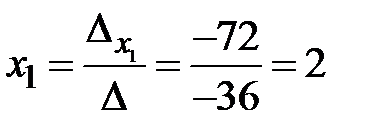 ,
, 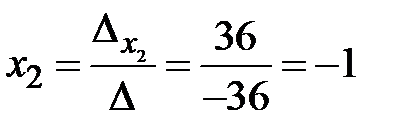 ,
, 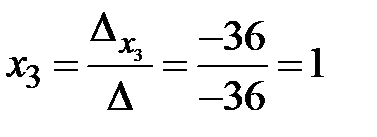 . ►
. ►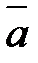
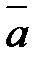 или
или 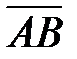 (т.
(т. 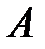 – начало, т.
– начало, т. 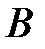 – конец вектора). Длина (модуль, норма, абсолютная величина) вектора обозначается
– конец вектора). Длина (модуль, норма, абсолютная величина) вектора обозначается 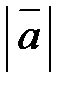 или
или 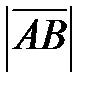 .
. 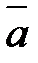
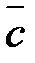
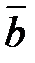
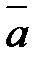 ,
, 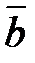 и
и 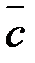 – коллинеарные;
– коллинеарные; 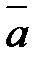 и
и 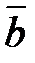 – однонаправлены,
– однонаправлены, 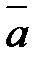 и
и 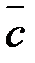 – противоположно направлены.
– противоположно направлены.  – вектор, у которого конец и начало совпадают (его модуль
– вектор, у которого конец и начало совпадают (его модуль 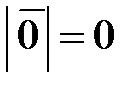 ).
).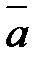 =
= 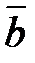 ,
,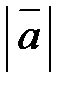 =
= 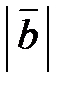 ).
).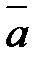 , обозначается через –
, обозначается через – 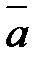 (
( 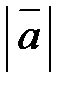 =
= 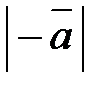 ). Из определения противоположного вектора следует –(–
). Из определения противоположного вектора следует –(– 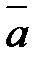 )=
)= 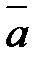 .
.
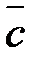
 можно задать любым вектором, лежащим на ней и имеющим то же направление (рис. 3).
можно задать любым вектором, лежащим на ней и имеющим то же направление (рис. 3). 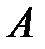 на ось
на ось  есть основание
есть основание 
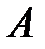
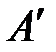
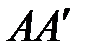 (точка
(точка 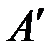 ), опущенного из т.
), опущенного из т. 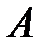 на эту ось (рис. 4).
на эту ось (рис. 4). 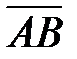 на ось
на ось  называется вектор
называется вектор 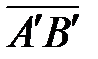 , где
, где 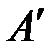 – проекция начала, а
– проекция начала, а 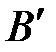 – конца на эту ось (рис. 4.5). Компоненту вектора называют также геометрической проекцией вектора на ось (обозначают
– конца на эту ось (рис. 4.5). Компоненту вектора называют также геометрической проекцией вектора на ось (обозначают 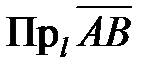 ). Если ось
). Если ось  задана вектором
задана вектором 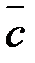 , то вектор
, то вектор 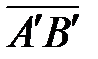 называется также компонентой (геометрической проекцией
называется также компонентой (геометрической проекцией 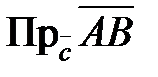 ) вектора
) вектора 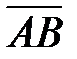 на направление вектора
на направление вектора 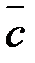 .
.
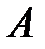
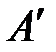
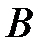
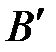
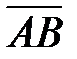 на ось
на ось  (или на направление вектора
(или на направление вектора 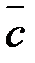 ) называется длина вектора
) называется длина вектора 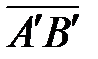 (см. рис. 5), взятая со знаком “+”, если вектор
(см. рис. 5), взятая со знаком “+”, если вектор 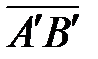 имеет то же направление, что и ось
имеет то же направление, что и ось  , или “–“, если ― противоположное направление. Проекция обозначается
, или “–“, если ― противоположное направление. Проекция обозначается 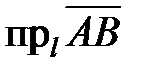 или
или 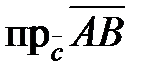 . Для случая, представленного на рис. 5, проекция вектора
. Для случая, представленного на рис. 5, проекция вектора 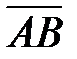 на ось
на ось  будет иметь отрицательный знак.
будет иметь отрицательный знак. 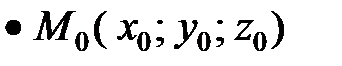

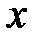
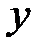
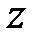
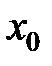
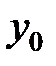
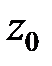
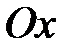 ,
, 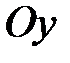 и
и 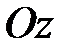 , пересекающихся в начале координат
, пересекающихся в начале координат  , при заданной единице масштаба для всех трех осей (рис. 6). Название осей:
, при заданной единице масштаба для всех трех осей (рис. 6). Название осей: 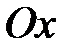 – ось абсцисс,
– ось абсцисс, 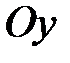 – ось ординат,
– ось ординат, 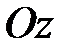 – ось аппликат.
– ось аппликат. 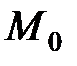 есть расстояния ее проекций
есть расстояния ее проекций 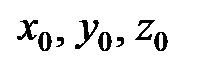 (рис. 6) на координатные оси от начала координат, взятые со знаком “+”, если проекция лежит по отношению к началу в положительном направлении оси, и со знаком “–“, если ― в отрицательном. Обозначение координат точки:
(рис. 6) на координатные оси от начала координат, взятые со знаком “+”, если проекция лежит по отношению к началу в положительном направлении оси, и со знаком “–“, если ― в отрицательном. Обозначение координат точки:  .
.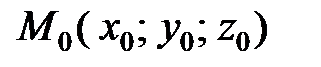

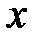
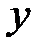
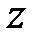
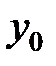
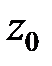
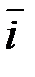
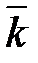
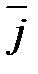
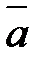
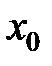
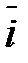 ,
, 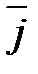 ,
, 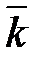 осей
осей 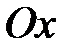 ,
, 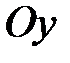 и
и 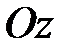 соответственно (рис. 4.7) образуют систему базисных векторов (базис (ортонормированный)). Эти единичные векторы попарно перпендикулярны друг другу и носят название базисных векторов.
соответственно (рис. 4.7) образуют систему базисных векторов (базис (ортонормированный)). Эти единичные векторы попарно перпендикулярны друг другу и носят название базисных векторов. 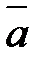 есть его алгебраические проекции на оси координат. Если начало вектора совмещено с началом координат (рис. 7), то координатами вектора будут координаты его конца. Запись координат вектора:
есть его алгебраические проекции на оси координат. Если начало вектора совмещено с началом координат (рис. 7), то координатами вектора будут координаты его конца. Запись координат вектора: 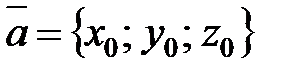 .
.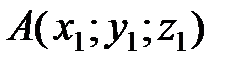
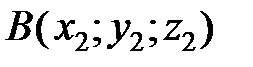
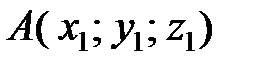 является началом вектора
является началом вектора 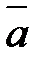 , а точка
, а точка 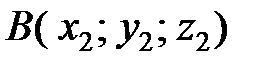 ― его концом (рис. 8), то
― его концом (рис. 8), то 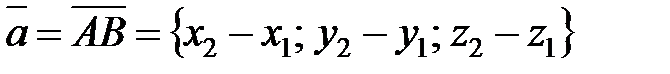 , (1)
, (1)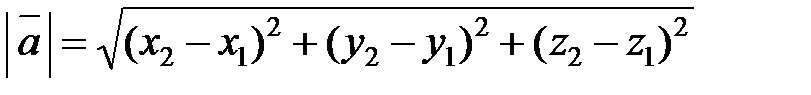 . (2)
. (2)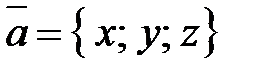

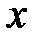
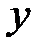
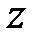
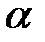
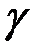
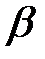
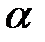 ,
, 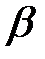 ,
, 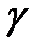 , образуемые положительными направлениями координатных осей
, образуемые положительными направлениями координатных осей 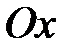 ,
, 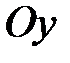 и
и 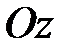 с вектором
с вектором 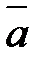 (рис. 9). Косинусы этих углов называются направляющими косинусами вектора:
(рис. 9). Косинусы этих углов называются направляющими косинусами вектора: 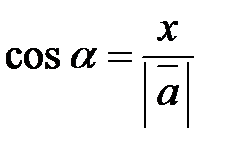 ,
,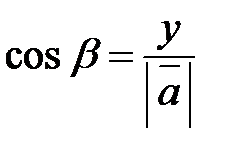 , (3)
, (3)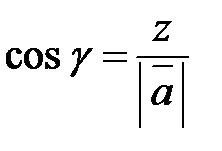 .
.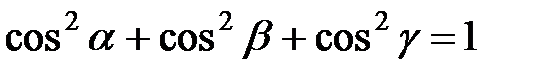 . (4)
. (4)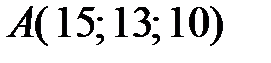 в точку
в точку 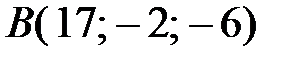 .
.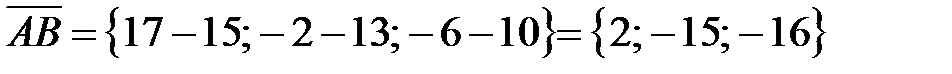 . Согласно (2) длина вектора
. Согласно (2) длина вектора 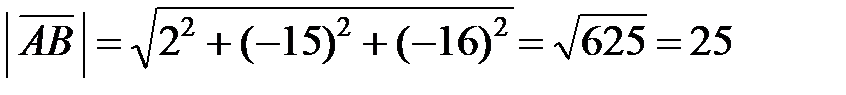 . По формулам (4.3) находим направляющие косинусы:
. По формулам (4.3) находим направляющие косинусы: 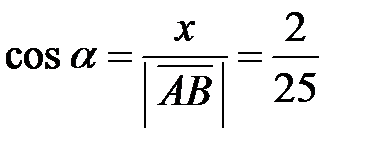 ,
, 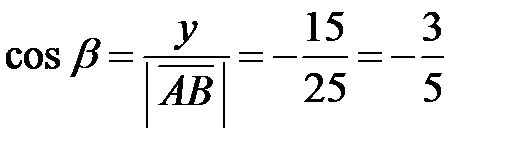 ,
, 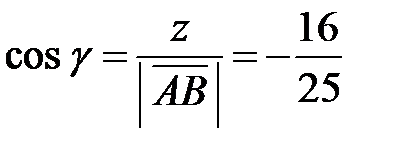 . Проводим проверку на основе равенства (4):
. Проводим проверку на основе равенства (4): 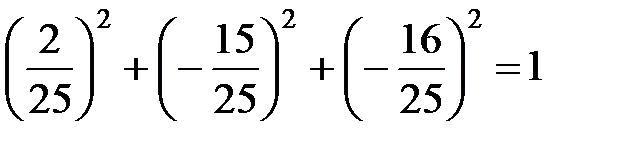 ►
►