Деление отрезка в заданном отношении

Линейные операции с векторами

Основы теории

Правило "конец минус начало"

Векторное равенство 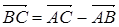является следствием формулы сложения векторов 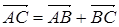. Если задано начало отсчета O, то с каждой точкой M связывают ее радиус-вектор 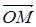. Тогда для двух точек M₁ и M₂ вектор 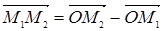. Положение на­чала отсчета часто бывает несущественно, тогда это равенство можно записать несколько иначе: 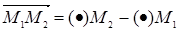(правило “конец минус начало”).

Базис и координаты

Базис на плоскости состоит из двух неколлинеарных векторов e₁ e₂. Любой вектор a можно разложить по базису: a = a₁×e₁ + a₂×e₂. Координатами вектора a в базисе e₁, e₂ называются коэффициенты a₁, a₂ в разложении этого вектора. Координаты вектора определяются однозначно. Если базис зафикси­рован, вектор можно кратко записать через его координаты a = {a₁, a₂}.

Базис в трехмерном пространстве состоит из трех некомпланарных векторов
e₁, e₂, e₃. Любой вектор a можно разложить по базису: a=a₁×e₁+a₂×e₂+a₃×e₃.. Координатами вектора a в базисе e₁, e₂, e₃ называются коэффициенты a₁, a₂, a₃ в разложении этого вектора. Координаты вектора определяются однозначно. Если базис зафиксирован, вектор можно кратко записать через его координаты a = {a₁, a₂, a₃}.

При сложении (вычитании) векторов соответствующие координаты складываются (вычитаются), при умножении вектора на число все его координаты умножаются на это число. Это справедливо как для координат на плоскости, так и в трехмерном пространстве.

Система координат на плоскости (в трехмерном пространстве) определяется заданием начальной точки O и базиса e₁, e₂ (e₁, e₂, e₃). Ориентированные прямые, несущие базисные векторы, называются осями координат. Обычно их обозначают Ox, Oy, Oz.

С каждой точкой M связывают ее радиус-вектор 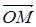. Его координаты в базисе, связанном с системой координат, называются координатами точки M. Если 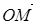= x×e₁+y×e₂+z×e₃, координаты точки M записываются в виде M(x,y,z). (На плоскости берутся только координаты x,y). Если заданы две точки M₁(x₁,y₁,z₁) и M₂(x₂,y₂,z₂), то вектор 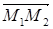={x₂–x₁, y₂–y₁, z₂–z₁}.

Деление отрезка в заданном отношении

Дан отрезок M₁M₂ и число l. Требуется найти на отрезке такую точку M, что отношение длин .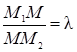

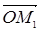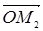Будем считать, что точки M₁ и M₂ заданы их радиус-векторами относительно некоторой точки O: = r₁, = r₂ и будем искать радиус- век­тор 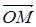=r.

Отношение длин запишем в векторной форме: 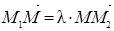, по пра­вилу "конец минус начало" имеем 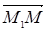= r – r₁, 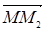= r₂– r, откуда

r – r₁= l×(r₂– r).

Разрешив это уравнение относительно неизвестного вектора r, получим формулу деления отрезка в заданном отношении в векторной форме:

,

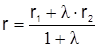в координатной форме , , ,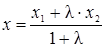

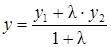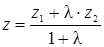Важный частный случай: при l=1 имеем деление отрезка пополам:

,

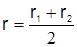в координатной форме , , .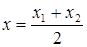

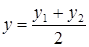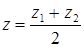В первона­чаль­ной поста­новке задачи отношение l > 0, но это ограничение можно снять, считая l любым, отличным от –1. При l > 0 говорят, что отрезок де­лится внутренним образом, а при l < 0 – внешним образом. На рисунке показаны положения точки M при некоторых значениях l; при l® –1 точка M "уходит в бесконеч­ность".

Центр тяжести (центр масс)

Точка P – центр тяжести системы двух материальных точек P₁, P₂ с массами m₁, m₂ делит отрезок P₁P₂ в отношении, обратном отношению масс: .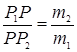

Центр тяжести системы материальных точек P₁, P₂,¼ с массами m₁, m₂,¼ – точка С, радиус-вектор которой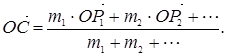

Центр тяжести однородного отрезка – его середина, масса отрезка про­пор­циональна его длине. Пусть имеется система однородных отрезков с дли­нами
L₁, L₂,¼ и центрами тяжести C₁, C₂,¼ Заменив каждый отрезок материальной точкой, расположенной в его центре тяжести, сведем задачу к задаче о центре тяжести системы материальных точек.

Центр тяжести од­но­род­ного пря­мо­угольника – его геометрический центр (точка пересечения диа­го­налей, она же точка пересечения средних линий). Центр тяжести од­но­род­ного треугольника – точка пересечения ме­диан. Пусть имеется пла­стинка, ко­торую мож­но разбить на несколько фигур с площадями
S₁, S₂,¼и центрами тяжести C₁, C₂,¼ Заменив каждую фигуру материальной точкой, расположенной в центре тяжести и имеющей массу, пропорциональную площади, сведем задачу к задаче о центре тяжести системы мате­риальных точек.

Решение задач

Р 2.1. (Мод 109) Даны две вершины треугольника ABC: A(–4,–1,2) и B(3,5,–16). Найти третью вершину C, зная, что середина стороны AC лежит на оси Oy, а сере­дина стороны BC – на плоскости Oxz.

Решение. Пусть координаты третьей вершины C(x,y,z), тогда коорди­наты середины стороны AC суть 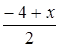, , 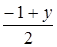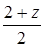. По условию эта точка лежит на оси Oy, поэтому 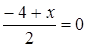, , 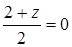откуда y = 4, z = –2. Координаты середины стороны BC суть 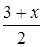, , 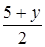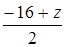. По усло­вию эта точка лежит на плоскости Oxz, поэтому 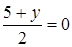, откуда y = –5. Та­ким образом, имеем
C(4,–5,–2).

Р 2.2. Найти точку M пересечения медиан треугольника ABC.

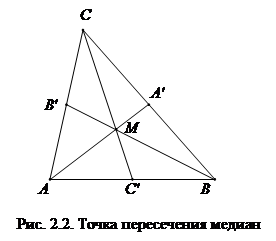Решение. Радиус-векторы вершин тре­угольника суть 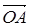, , 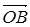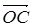. Радиус-вектор точки C' (середины стороны AB) 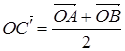. По теореме школьной геометрии точка пересечения медиан делит отрезок CC' в отноше­нии l = 2, поэтому

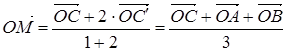
(среднее арифметиче­ское).

В координатах

, , .

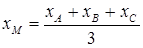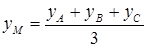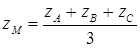Р 2.3. (Мод 11) На стороне AD параллелограмма ABCD отложен вектор 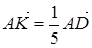, а на диагонали AC – вектор 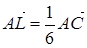. Докажите, что век­торы 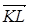и 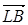коллинеарны и найдите коэффициент l в соотношении .

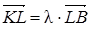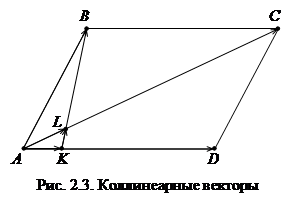Решение. Выразим все векторы через два базисных вектора 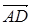и 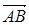. Имеем 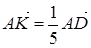, , 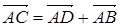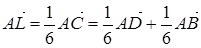. Векторы 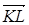и 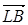выразим по правилу "конец минус начало":

,

.

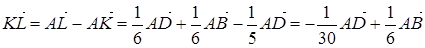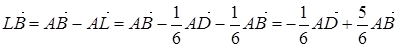Сравнивая разложения векторов 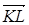и 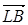по базису, видим, что 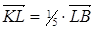, т.е. эти векторы коллинеарны, коэффициент .

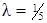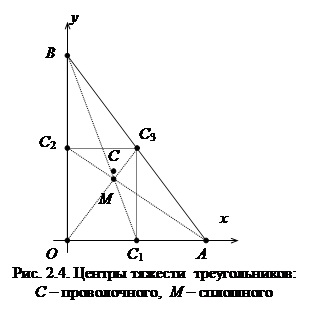Р 2.4. (Мод 106) Найти координаты центра тяжести проволочного тре­угольника со сторонами 3, 4, 5. Ось Ox направлена по меньшему катету, ось Oy – по большему катету.

Решение. Длины и координаты цен­тров тяжести сторон треугольника OAB:

OA : L₁=3, C₁( 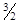,0);

OB : L₂=4, C₂(0,2);

AB : L₃=5, C₃( 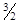,2).

По формуле находим координаты точ­ки C (центра тяжести проволоч­ного тре­угольника):

,

.

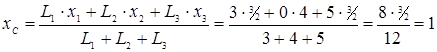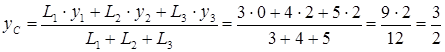Замечание. Центр тяжести треугольника OAB, вырезанного из однородного плоского материала – точка пересечения медиан M. Для любого треугольника ко­ординаты этой точки суть средние арифметические координат вершин треуголь­ника (см. Р 2.2)

, .

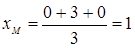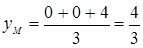Видим, что точки C и M не совпадают. Если в вершинах разместить равные (например, единичные) массы, центр тяжести такой системы материальных точек также будет находиться в точке M.

Еще один способ получить ту же точку M: счи­тать, что в вершинах треугольника C₁C₂C₃ расположены равные массы, не завися­щие от длин сторон, и найти точку пересечения медиан этого треугольника.

Р 2.5. Найти координаты центра тяжести однородной пла­стинки (размеры указаны на рис. 2.5).

Решение. Площади и координаты цен­тров тя­жести трех прямоуголь­ни­ков, на ко­торые разби­та пластинка, суть

x₁=10, y₁=5, S₁=200; x₂=10, y₂=20, S₂=400; x₃=25, y₃=20, S₃=200.

Подставив эти числа в фор­мулу, найдем коорди­наты цен­тра тяжести пла­стинки

x=13.75, y=16.25,

он лежит на оси симмет­рии пластинки (см. рис. 2.5).

Замечание. Данную задачу можно решить без всяких вычислений, простыми геометри­че­ски­ми по­строениями (см. рис. 2.6). Объеди­ним пер­вый и второй прямо­угольни­ки в один и найдем его центр тяжести (на рисунке это точка C₁₂). Очевидно, что центр тяжести пластинки лежит на отрезке, соединяющем эту точку с цен­тром тяжести третьего прямо­угольника C₃. Таким же образом найдем общий центр второго и третьего прямоугольника (на рисунке это точка C₂₃). Центр тяжести пластинки ле­жит на отрезке, соединяющем эту точку с центром тяжести первого прямоуголь­ника C₁. Окончательно приходим к выводу: центр тяжести пластинки C – точка пересечения от­резков C₁₂C₃. и C₁C₂₃.