Динамиканың бірінші және екінші есептері
Нүкте динамикасында негізгі екі есеп бар. Оның біріншісінде материялық нүкте қозғалысының заңы және оның массасы m беріледі. Осы заңдылықта болатын қозғалысты тудыратын күшті табу керек болады. Екінші мәселеде берілген күш бойынша массасы m-ге тең нүкте қозғалысының заңын анықтау керек.
Динамиканың бірінші есебі.Нүкте динамикасының бірінші есебін шешу көп қиыншылық тудырмайды. Бірінші есепте нүкте массасы m және оның қозғалысының кинематикалық теңдеулері
.
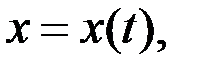
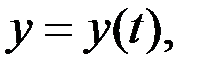
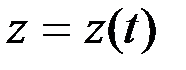берілген болады. Осы берілгендер арқылы (3.7) теңдеулерінен іздеп отырған күштің проекциялары табылады:
.
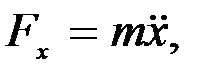
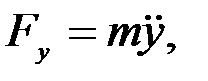
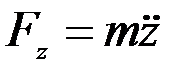Осы күш проекциялары арқылы күштің өзін анықтап аламыз.
1-мысал.Салмағы 1.02 кГ жүк жатқан горизонталь платформа 4 м/с2 үдеумен вертикаль төмен қозғалады (3.3-сурет). Олар бірге қозғалғанда жүктің платформаға түсіретін қысым күшін табу керек.
Шешуі. Жүкке бір ғана актив күші түсірілген – оның салмағы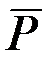 
. Байланыстардан босату аксиомасын пайдаланып, ойша платформаны алып тастаймыз да, оның әсерін вертикаль жоғары бағытталған 
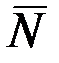реакция күшімен ауыстырамыз.
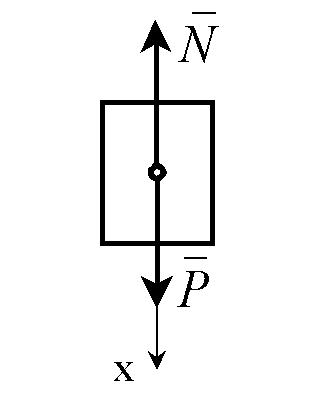
3.3-сурет
x–өсін вертикаль төмен қозғалыс бағытымен бағыттаймыз (3.3-сурет). Жүктің негізгі теңдеуі мына түрде жазылады:
ma = P – N,
осы теңдеуден:
N = P – ma = 1.02 × 9,8 – 1.02 × 4 = 5.92 Н.
Яғни жүктің платформаға түсіретін қысым күші де 5.92 Н-ға тең болады.
2-мысал.Массасы 2кг материалық нүктенің қозғалысы мына теңдеулермен анықталады:
, 
.
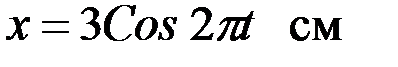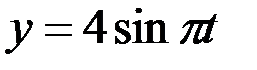Нүктеге әсер етуші күштің проекцияларының нүкте координаттарына тәуелділігін анықтау керек..
Шешуі. Алдымен нүкте үдеуінің проекцияларын табамыз. Ол үшін есептің шартында берілген қозғалыс теңдеулерінен уақыт бойынша екі рет туынды аламыз:
.
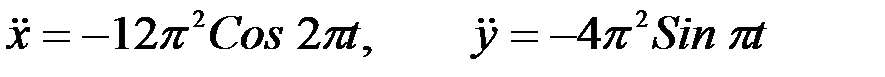Нүкте қозғалысының дифференциалдық теңдеулерін пайдалану арқылы күштің координаттар өстеріндегі проекцияларын табамыз:
.
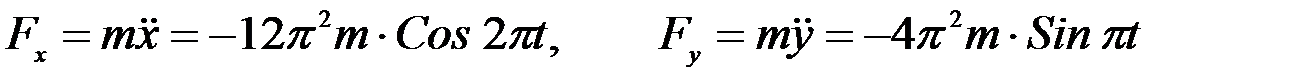Сан мәндерін орындарына қойып, нүктеге әсер етуші күштің проекцияларының нүкте координаттарына тәуелділігін анықтаймыз:
.
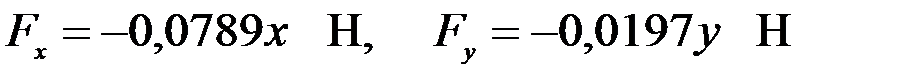Нүкте динамикасының екінші есебі. Нүкте динамикасының екінші есебін шешу екінші ретті үш дифференциалдық теңдеулер жүйесі (3.7)-ні интегралдауға келтіріледі. Дифференциалдық теңдеулердің мұндай жүйесінің жалпы шешімі әлі табылмаған. Сондықтан біз ол жүйені шешудің жалпы сұлбасын көрсетіп өтейік. Бізге массасы m-ге тең материялық нүктенің берілген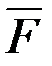 
күші әсерінен болатын қозғалысының дифференциалдық теңдеулері (3.7) берілсін:
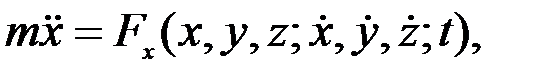
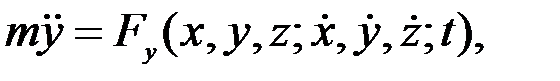(3.8)
.
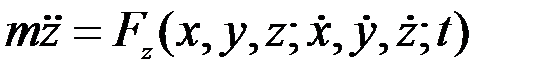Берілген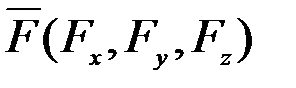 
әсерінен болатын нүкте қозғалысын табу (3.8) дифференциалдық теңдеулер жүйесін шешуге келтіріледі. Ол теңдеулерді түрлендіру нәтижесінде мынадай үш теңдеулер алдық дейік:
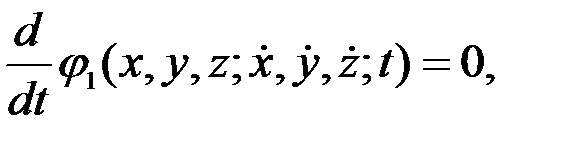
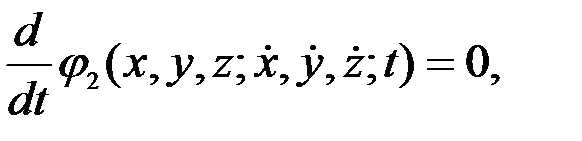(3.9)
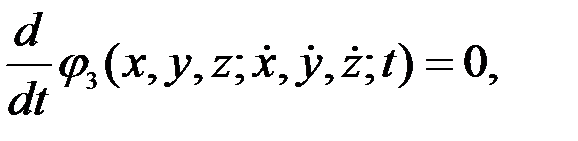
Онда (3.9)-ды интегралдау арқылы, мынадай бірінші интегралдарды алған болар едік.
,
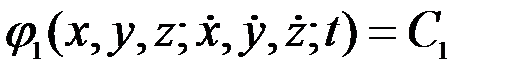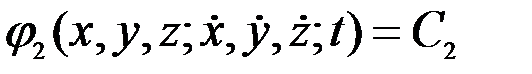, (3.10)
.
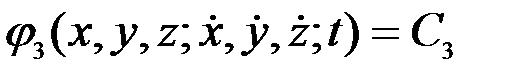(3.10)-дағы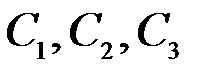 
-тұрақтылары, интегралдаудың кез келген тұрақтылары деп аталады.
(3.10) теңдеулерін тағы да бір рет интегралдап шығуымыз керек. Сол мақсатпен оларды қалай да түрлендіре отырып, мынадай түрге келтіре алдық дейік:
,
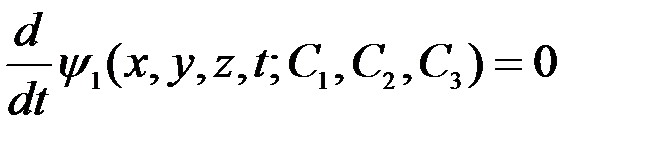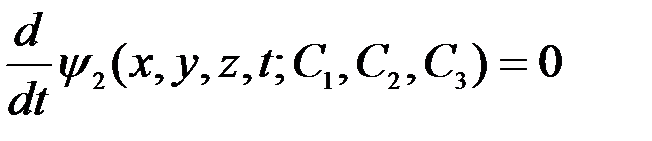, (3.11)
.
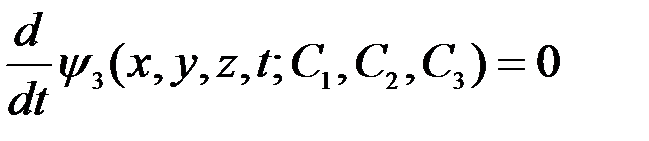Онда бұларды оңай интегралдаған болар едік те, мынадай қатынастар алар едік:
,
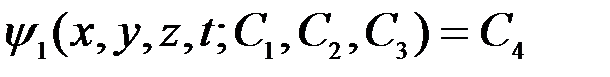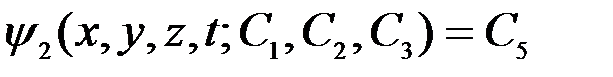, (3.12)
.
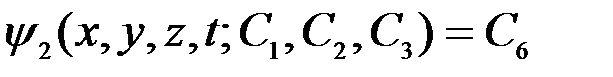мұндағы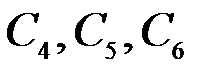 
- интегралдау тұрақтыларының келесі үшеуі.
Уақыт, координаттар, кез келген тұрақты шамалар арасындағы тәуелділікті беретін және қозғалыс теңдеулері негізінде орынды болатын, (3.12) түріндегі қатынастарды қозғалыс теңдеулерінің екінші интегралдары деп атайды. (3.12) қатынастарынан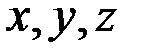 
-терді табуға болады:
,
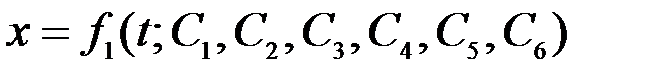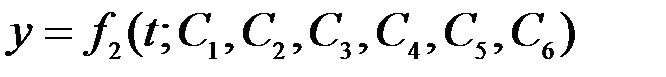, (3.13)
.
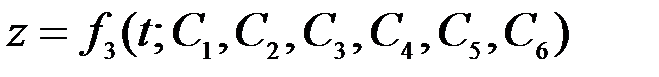(3.13) теңдіктері (3.8) қозғалыс теңдеулерінің жалпы шешімі болып табылады. Мұнда нүкте координаттары уақытқа және алты кез келген тұрақты шамаларға тәуелді функциялар ретінде анықталған.
Сонымен, жалпы жағдайда нүкте координаттары алты кез келген тұрақты шамаларға тәуелді болып шықты.
Басқаша айтқанда, қозғалыс теңдеулерін интегралдау арқылы материялық нүктенің берілген күш әсерінен мүмкін болатын қозғалыстарының барлығының да заңдарын табуға болады екен.
Мысалы, біз материялық нүктені ауасыз ортада бір орыннан әр түрлі бағыттағы жылдамдықпен ұшыруымызға болады. Онда ол нүкте ауырлық күші әсерінен бастапқы жылдамдықтың қалай бағытталуына байланысты түзу сызық бойымен немесе әр түрлі параболалар бойымен қозғалуы мүмкін.
Сол себепті күштің өзгеру заңдылығын
,
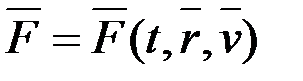көрсетумен қатар, нүктенің бастапқы орны мен жылдамдығын да нақтылы көрсетіп отыруымыз қажет.
Уақыт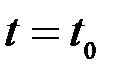 
болғанда , нүктенің бастапқы орнын анықтайтын координаттар мынадай болды дейік:
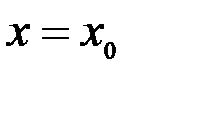
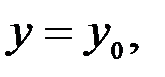
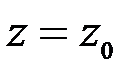, (3.14)
Ал бастапқы жылдамдық проекциялары мынадай болсын:
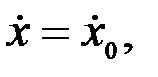
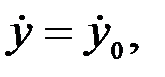
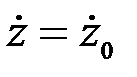(3.15)
(3.14) және (3.15) қатынастарының жиынын бастапқы шарттар деп атаймыз. Осы бастапқы шарттар арқылы интегралдау тұрақтылары табылады. Ол үшін (3.10) және (3.12) теңдеулердегі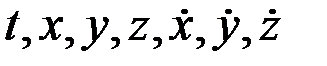 
айнымалылары орнына олардың (3.14) және (3.15)-теңдеулерде көрсетілген бастапқы мәндерді қоямыз. Сонда:
,
,
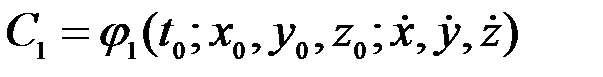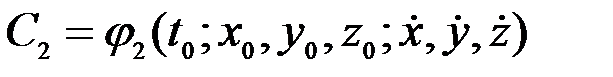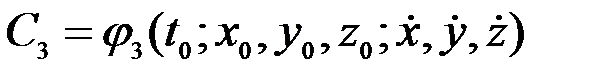, (3.16)
,
,
.
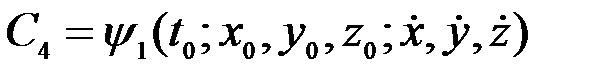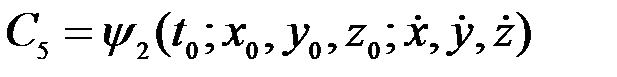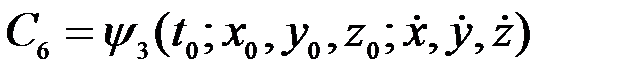(3.16) бойынша анықталатын интегралдау тұрақтыларының мәндерін (3.13) –теңдеуге қойсақ, мынаны аламыз:
,
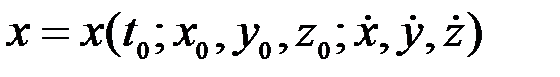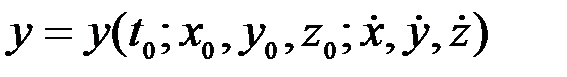, (3.17)
.
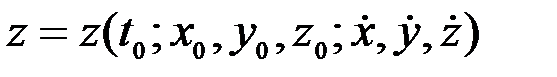(3.17)-теңдіктер берілген күш әсерінен болатын және бастапқы шарттарға сәйкес орындалатын нүкте қозғалысының заңын анықтайды. Сонымен нүкте динамикасының екінші есебінің шешілуі осы сұлба бойынша жүргізіледі.