Кривые поверхности. точки на поверхностях

В начертательной геометрии поверхность рассматривают как геометрическое место последовательных положений линии (образующей), движущейся в пространстве по определенному закону.

Кривые поверхности по виду образующей можно разделить на два класса:

- линейчатые, образующая которых является прямая линия;

- нелинейчатые, образованные движением кривой.

К линейчатым поверхностям относятся, например:

- конические – прямолинейная образующая проходит через вершину конической поверхности и последовательно все точки некоторой кривой (направляющей).

- цилиндрические – прямолинейная образующая во всех своих положениях параллельна некоторой заданной прямой и последовательно проходит через все точки некоторой кривой (направляющей).

- винтовые – прямолинейная образующая проходит последовательно через все точки пространственной кривой – винтовой линии и пересекает ось винтовой линии под постоянным углом.

а) б) в) Рис. 9.1

На рис. 9.1 приведены примеры некоторых линейчатых поверхностей: конуса (а), цилиндр (б), прямой геликоид (в).

При вращении образующей вокруг неподвижной оси получается поверхность, называемая поверхностью вращения. Каждая точка этой поверхности описывает около оси окружность, следовательно, любая плоскость, перпендикулярная оси вращения, пересечет поверхность вращения по окружности с центром на этой оси. Эти окружности называются параллелями (рис. 9.2). Наибольшую из параллелей называют экватором, наименьшую – горлом.

Плоскость, проходящая через ось поверхности вращения называется меридиональной, а линия пересечения этой плоскости с поверхностью вращения – меридианом поверхности. Если ось поверхности вращения перпендикулярна плоскости p₁, то меридиан, лежащий во фронтальной плоскости называется фронтальным меридианом, а в профильной, соответственно, профильным меридианом.

На рис. 9.3. приведены некоторые поверхности вращения: конус вращения (а), цилиндр вращения (б), сфера (в).

Если точка лежит на поверхности, то проекции точек принадлежат линиям поверхности.

На рис. 9.1 (а) точка А на поверхности конуса лежит на образующей S1, соединяющей вершину S с точкой на основании 1.

На рис. 9.1 (б) точка В на поверхности цилиндра лежит на образующей, проходящей через точку 1 и параллельной оси круговых сечений i.

На рис. 9.1. (в) точка М на винтовой поверхности лежит на образующей, соединяющей точку 1 винтовой линии m с осью i и проходящей параллельно плоскости p₁.

На рис. 9.3. (а, б, в) точки А, В, С на соответствующих поверхностях лежат на параллелях этих поверхностей, а точки M и N на фронтальных меридианах (очерковых линиях) конуса и сферы соответственно.

Рис. 9.2

а) б) в) Рис. 9.3

Задачи

9.1.1. Построить проекции цилиндра, заданного его основанием и горизонтальной проекцией образующей А₁В₁. Точка М лежит на поверхности цилиндра.

9.1.2. Построить проекции сферы, если даны проекции центра сферы 0 и точки М, лежащей на этой сфере.

9.1.3. Построить проекции конуса вращения с вершиной в данной точке S и основанием лежащим в плоскости 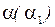. Радиус основания равен высоте конуса.

9.1.4. Построить проекции конуса вращения, ось которого лежит на прямой а. Высота конуса равна l, окружность основания касается плоскости .

9.1.5. Найти недостающие проекции точек A,B,C,D на поверхности сферы (а); M,N,P на поверхности цилиндра (б); E,F,K,L на поверхности тора (в).

9.1.6. Построить фронтальную проекцию линии АВ на поверхности конуса вращения (а); горизонтальную проекцию линии MN на поверхности наклонного цилиндра (б); горизонтальную и профильную проекции линий АВС на поверхности сферы (в).

9.1.7. Поворотом вокруг оси i точку А совместить с поверхностью сферы (а), а точку В- с поверхностью тора (б).