Расчет пространственных ферм
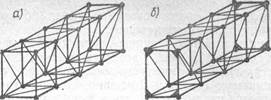
Рис. 3
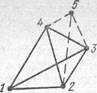 |
Рис. 4
Шарнирной фермой называется пространственная неизменяемая система, состоящая из прямых стержней, соединенных по концам шаровыми шарнирами. При узловой нагрузке в стержнях шарнирной фермы возникают только продольные силы. В основе образования простых ферм лежит тетраэдр (рис. 3). Каждый новый узел фермы образуется тремя стержнями, не лежащими в одной плоскости, так как иначе присоединяемый узел будет иметь бесконечно малое или конечное перемещение по направлению, перпендикулярному плоскости стержней. Такое же перемещение будет иметь узел с любым числом стержней, лежащих в одной плоскости.
Степень статической неопределимости пространственной системы (фермы), т.е. число i, показывающее, на сколько единиц количество неизвестных превосходит возможное число независимых уравнений статики, равна:
i = S + S0 – 3Y,
где S – число стержней системы;
S0 – число опорных связей;
Y – число шарнирных узлов.
Если i 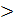 0, то система статически неопределима;
0, то система статически неопределима;
i = 0, то система статически определима;
i < 0, то система изменяема (механизм).
Условие i = 0 необходимое, но недостаточное (необходим геометрический анализ структуры системы).
Для расчета пространственных систем могут быть использованы способы простых и совместных сечений, метод замены связей, кинематический метод, способ вырезания узлов (для ферм). Содержание этих способов и методов не меняется, но применение их к пространственным системам значительно сложнее, поскольку равновесие рассматривается в пространстве.
Способ простых сечений состоит в том, что система воображаемой поверхностью, проведенной через шесть связей, разделяется на две части и рассматривается равновесие одной из них. Если система неизменяема, то все неизвестные могут быть найдены из шести уравнений равновесия. При этом рекомендуется составлять уравнения равновесия в виде суммы моментов относительно двух прямых, которые пересекают четыре силы. Это дает возможность определить остальные два неизвестных из двух уравнений. В отдельных случаях могут быть использованы и уравнения в виде суммы проекций сил на ось, которую следует выбирать с таким расчетом, чтобы возможно большее число неизвестных сил исключалось из этого уравнения. Если при рассечении системы на две части число неизвестных сил в рассеченных стержнях больше шести, то их определение по одному сечению невозможно. В этом случае используется способ совместных сечений.
Метод замены связей состоит в том, что в сложной системе удаляется одна или большее число связей, которые вводятся в других местах системы, с тем, чтобы новая система была проще заданной. Преобразованная система нагружается заданной нагрузкой и неизвестными реакциями отброшенных связей. Затем реакции заменяющих связей от действующей нагрузки и неизвестных сил приравниваются нулю, так как в действительности таких заменяющих связей нет.
Кинематический метод состоит в том, что из системы выбрасывается связь и ее действие на систему заменяется неизвестной реакцией. Полученной изменяемой системе задается бесконечно малое возможное перемещение, на котором составляется уравнение работ. Из этого выражения определяется искомая реакция связи.
Способ вырезания узлов (для ферм) есть разновидность способа сечений, в котором от фермы отсекается один узел. Для сил, сходящихся в узле, составляются только три независимых уравнения равновесия, причем каждое может быть или суммой проекций сил на ось, или суммой моментов сил относительно оси, пересекающей не менее двух стержней. Если в узле сходятся только три стержня, то продольные силы в каждом из них могут быть определены из уравнений равновесия этого узла. В таком случае можно рекомендовать уравнения равновесия записывать в виде суммы проекций сил на ось, перпендикулярную к плоскости каких-либо двух стержней, или в виде суммы моментов относительно оси, их пересекающей, что даст уравнение с одной неизвестной продольной силой третьего стержня.
Расчет простых ферм, в которых всегда имеется узел с тремя стержнями, надо начать с вырезания этого узла. Далее следует переходить к тем узлам, где не более трех неизвестных продольных сил, каждая из которых может быть определена из одного уравнения равновесия. По способу вырезания узлов, вообще говоря, может быть рассчитана любая ферма.
Способ вырезания узлов позволяет установить следующие правила определения неработающих стержней: 1) если в узле сходятся три стержня и в узле нет нагрузки, то продольные силы во всех трех стержнях равны нулю; 2) если в узле сходится n стержней, причем n – 1 этих стержней лежат в одной плоскости, то продольная сила в примыкающем стержне равна нулю, когда в узле нет нагрузки или она расположена в плоскости остальных стержней.
