Функцияның негізгі қасиеттері

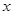1. Анықтама.Егер аралығында жатқан барлық нүктелері үшін теңсіздігі орындалатындай 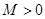саны табылса, онда функциясы аралығында шектелген функция деп аталады. Дербес жағдайда, болғанда шарты 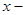айнымалысының шектеулігін көрсетеді.

Аралықта өсетін және кемитін функциялар

Анықтама. сегментінде (аралығында) анықталған функциясы үшін , болғанда теңсіздігі орындалса, онда осы аралықта өспелі (кемімелі) функция деп аталады.

Функция аралықта өспелі немесе кемімелі болса, онда бұл аралық монотондық аралық, ал функциясы осы аралықта монотонды деп аталады.

Мысал. функциясы аралығында монотонды және: интервалында кемімелі, ал интервалында өспелі.

3. Жұп және тақ функциялар.

а) болса, - жұп функция;

б) болса, - тақ функция.

4. Периодты функциялар. облысында анықталған фукциясы үшін саны табылып, , , теңдігі орындалса, онда периодты функция деп аталады.

5. Kүрделі функция . функциясының анықталу облысы , мәндер жиыны болсын, ал айнымалысы жиынында анықталған 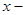ке тәуелді, мәндер жиыны болатын функция болсын: . Сонда жиынында берілген, мәндер жиыны болатын функциясы күрделі функция деп аталады.

Мысалы, күрделі функция, өйткені оны былай жазуға болады: .

6. Kері функция. функциясының анықталу облысы , ал мәндер жиыны болсын. Әрбір мәніне теңдігі орындалатындай бір мәнін сәйкес қойсақ, онда жиынында анықталған, ал мәндер жиыны болатын функциясы анықталады. Осы функция функциясының кері функциясы деп аталады және ол түрінде жазылады. және функциялары өзара кері функциялар деп аталады.

7. Белгісіз функция анық түрде берілмей, түрінде берілсе, онда тәуелділігі айқындалмаған функция деп аталады.

8. Функцияның параметрлік түрде берілуі. Егер 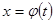функциясы үшін кері функция табылса, онда түрдегі тің 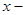ке тәуелді функциясын аламыз.

Ескерту: Функцияның параметр арқылы берілуі функцияның координат жүйесінде берілуінен көп тиімді, әрі кеңірек қолданылады.

Функцияның нүктедегі шегі

Анықтама. 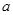нүктесінің маңайы осы нүкте жататын кез келген интервал.

Дербес жағдайда, 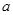нүктесінің маңайы − интервалы. маңайы түрінде белгіленеді.

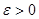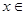
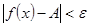Анықтама. Егер кез келген саны үшін саны табылып, кезкелген үшін теңсіздігі орындалса, онда 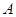саны функциясының 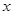шамасы 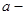ға ұмтылғандағы шегі деп аталады да, түрінде белгіленеді.

Ескерту: функциясы 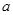нүктесінде анықталуы да, анықталмауы да мүмкін.

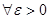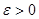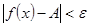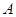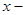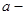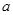Анықтама. Егер (кезкелген ) саны, үшін ( саны) табылып, үшін теңсіздігі орындалса, онда саны функциясының тің ға сол жақтан ұмтылғандағы шегі немесе функциясының нүктесіндегі сол жақ шегі делінеді. Белгіленуінде: .

Анықтама. Жоғарыдағыдай функциясының 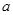нүктесіндегі оң жақ шегі деп аталады.