Закон Архимеда. Условие плавания тел.

S →0

lim означает предел; в пределе малая величина ∆ превращается в бесконечно малую δ (дифференциал).

Гидростатическое давление имеет два важных свойства:

-оно всегда направлено перпендикулярно к площадке;

-его действие не зависит от ориентации площадки в пространстве, т.е. со всех сторон оно одинаково.

2.2. Основное уравнение гидростатики.

В общем случае равновесия некоторого объёма жидкости под действием приложенных к нему сил знаменитым учёным Российской Академии наук Леонардом Эйлером было получено дифференциальное уравнение, решение которого позволяет получить расчётные формулы для нахождения гидростатического давления в разных конкретных случаях. Так, если на частицы жидкости действует только сила тяжести, то дифференциальное уравнение равновесия частиц внутри жидкости имеет следующий вид:

δ Р = - ρ gdz (2-4)

Здесь осьZ – вертикальная ось; ускорение свободного падения имеет направление, противоположное оси Z (на это указывает знак минус "–" в уравнении). Плотность жидкости ρ,как и ускорениеg , постоянные величины, не зависящие от давления и температуры

Решение (интегрирование) уравнения имеет следующий вид:

Р = - ρ gz + с (2-5)

Постоянную интегрирования находим следующим образом. Пусть рассматриваемая точка жидкости m находится на расстоянии Н от поверхности жидкости. При z = z₀ P = P₀

Следовательно, P₀ = - ρ gz + с Отсюда: с = P₀ + ρ gz₀ Подставляем значение с в формулу (2-5) и окончательно получаем формулу для расчёта гидростатического давления в точке, находящейся под слоем жидкости высотой Н:

Р = P₀ + ρ g Н (2-6)

Давление Р называют абсолютнымдавлением в точке, P₀ - внешнее поверхностное давление (в открытом сосуде оно равно атмосферному давлению),

Р - P₀ =P_в = ρ g Н – давление столба жидкости высотой Н (его также называют весовым или избыточным давлением). В технике приборами, как правило, измеряется избыточное давление.

В дальнейшем атмосферное давление условимся обозначатьР_атм, абсолютное – Р_А, а избыточное – Р_изб.

Выражение (2-6) называется основным уравнением гидростатики. Согласно этому уравнению, давление на поверхности жидкости P₀ передаётся всем точкам объёма жидкости и по всем направлениям одинаково (закон Паскаля – гиперссылка.

Из формулы (2-1) следует, что в системе СИ единицей измерения давления служит паскаль: Па = н/ м ² . Это небольшая величина и на практике часто используют более крупные единицы КПа=10³ Па и МПа=10⁶ Па.

2.3. Виды давления: атмосферное, избыточное, весовое, абсолютное, вакуумметрическое.

Атмосферное давление было открыто ещё в 16 в. известным итальянским учёным Торичелли. В земной атмосфере на любое тело, находящееся на поверхности земли давит воздушный столб. Его среднее давление Р = ρg Н определяется средней плотностью воздуха ρи высотой воздушного столбаН.Согласно измерениям Торичелли это давление соответствует давлению столба ртути высотой 733 мм. Более поздние исследования показали, что это давление (его назвали нормальным атмосферным давлением) составляет 760 мм.рт.ст. или в системе СИ -0,1013 МПа=101,3 КПа. Округлённо в расчётах его берут равным 100 КПа=0,1 МПа.

В закрытом сосуде над поверхности жидкости с помощью, например, компрессора, можно создать избыточное давление Р_изб. В этом случае абсолютное давление в точке под слоем жидкости на глубине Н будет равно:

Р_А = P₀ + ρ g Н = Р_атм + (Р_изб + ρ g Н)(2-7)

В подобных случаях давление столба жидкости принято называть весовым давлением. Из определения избыточного давления следует, что в закрытом сосуде на глубине Н оно складывается из Р_избвоздуха и весового P_в = ρ g Н (давления столба жидкости высотой Н).

Рисунок 2.1

Избыточное давление Р_изб в воздухе над поверхностью жидкости можно определить с помощью простого прибора, называемого пьезометром. Это стеклянная трубка малого диаметра, подсоединённая к сосуду с жидкостью (рис. 1-2). Из формулы (1-12) следует, что изменение величины P₀ одинаково для всех точек внутри жидкости. Если давление над поверхностью жидкости равно атмосферному (P₀ =Р_атм), то, согласно формуле (2-4) жидкость в трубке установится на той же высоте, что и в сосуде ( уровень 0-0). При увеличении давления

P₀ =P_атм+ Р_изб это избыточное давление Р_изб передаётся всем точкам жидкости, в том числе и тем, которые лежат на границе жидкость-воздух в трубке

(уровень 0-0; абсолютные давления в точках 1 и 2 одинаковы).

Р₀=Р_атм + Р 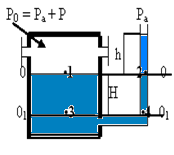Р_атм

Рис. 2.2. Схема измерения избыточного давления

Так как давление со стороны жидкости на них превысит давление воздуха P_атм, жидкость в трубке начнёт подниматься до нового положения равновесия (на высоту h). Следовательно, Р_изб = ρ gh.

За нулевой уровень можно принять любой другой уровень, например, проходящий на глубине Н (уровень 0₁-0₁). Абсолютные давления в точках 3 и 4 одинаковы .

Но P₃=P₀+ ρ g Н =P_атм+ Р + ρ g Н;

В данном случае давление Р является избыточным давлением Р =Р_изб.P₄=P_атм+ ρ gh + ρ g Н. Сравнивая правые части, снова получаем Р=Р_изб = ρ gh.

Пьезометры рассчитаны на измерение малых давлений (избыточное давление 0,1 ат поднимает воду в пьезометре на высоту 1 м).

Рассмотрим случай, когда абсолютное давление над поверхностью жидкости P_А становится меньше атмосферного (при откачивании воздуха из пространства над жидкостью), Давление в точке 1 при условии Р_А<Р_атм можно измерить с помощью, так называемого обратного пьезометра или вакуумметра (см. рис. 1-3). Очевидно, что горизонт жидкости в изогнутой трубке опустится ниже уровня точки 1 на высоту h_вак. Эта высота по отношению к уровню, проходящему через точку 1, будет отрицательной, если высоту Н считать положительной.

Давление в точке 1 сверху будет равно:

Р_А = Р₀ + ρ g Н.

Давление в точке 1 со стороны трубки 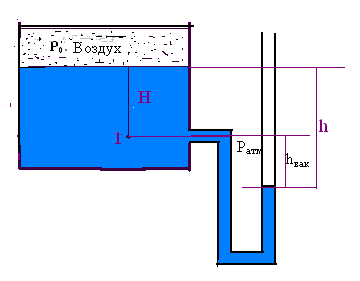равно:

Р_атм - ρ gh_вак.

Из равенства этих формул следует, что давление Р_А = Р_атм - ρ gh_вак. Отсюда

h_вак=(Р_атм – Р_А)/ ρ g.(2-8) Эту величину называют вакуумметрической высотой,

Рисунок 2.3. Схема измерения вакуумметрической высоты с помощью вакуумметра.

Она характеризует разность двух давлений Р_атм – Р_А в точке 1. Именно эту разность и называютвакуумом.

Избыточное давление в жидкости можно создать с помощью насос, оказывая на неё силовое действие (рабочим органом насоса). При движении рабочего органа (поршень, ротор и т.п.) на входе в насос образуется вакуум (разряжение), а нв выходе насоса-избыточное давление. Измеряются они с помощью приборов (манометров, мановакуумметров).

2.4. Давление жидкости на плоскую и цилиндрическую стенки.

Рис. 2.4. Схема к определению равнодействующей гидростатического давления на плоскую поверхность. Эпюра сил давления. Справа- развёрнутая поверхность стенки.

На плоскую стенку в сосуде с жидкостью действуют силы давления, направленные перпендикулярно к ней.

С ростом глубины погружения Н растёт и величина избыточного давления Р = ρ g Н, а, следовательно, и сила давления на стенку. Можно показать, что средняя сила давления на вертикальную стенку равна произве-дению давления в центре стенки на площадь стенки:

F = P_cS, где P_c = ρ gН_с= ρ g Н/2 (2-9)

Давление на горизонтальную поверхность дна сосуда во всех точках одинаково, поэтому сила давления на дно сосуда равна

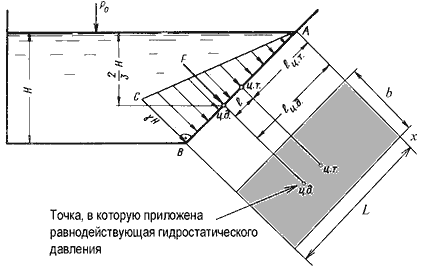
Рис.2.5.Эпюра сил давления для наклонной стенки.

F = P∙S, где P= ρ g Н (2-10)

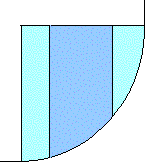
В случае криволинейных стенок чаще всего необходимо определить силу, действующую на цилиндрическую поверхность, имеющую вертикальную ось симметрии. Возможны два варианта. Первый вариант -жидкость воздействует на стенку изнутри.

Во втором варианте жидкость действует на стенку снаружи. Рассмотрим первый вариант.

Выделим объём жидкости, ограниченный рассматриваемым участком цилиндрической поверхности AB, участком свободной поверхности CD, расположенным над участком AB, и двумя вертикальными поверхностями BC и CD, проходящими через точки A и B. Эти поверхности ограничивают объём ABCD, который находится в равновесии. Рассмотрим условия равновесия этого объёма в вертикальном и горизонтальном направлениях. Заметим, что, если жидкость действует на поверхность AB,c какой то силой F, то с такой же силой, но в обратном направлении, и поверхность действует на рассматриваемый объём жидкости. Эту силу, перпендикулярную поверхности AB, можно представить в виде горизонтальной F_г и вертикальной F_в составляющих.

Условие равновесия объёма ABCD в вертикальном направлении выглядит, так: F_в = P₀S_г + G (2-10)

где P₀ – внешнее давление, S_г – площадь горизонтальной проекции поверхности AB, G – вес выделенного объёма жидкости.

Центр тяжести площадки AB

P0

hc

G

C

E

D

A

Fг

Fв

F

B

Рис.2.6. К определению силы давления на цилиндрическую стенку

Условие равновесия этого объёма в горизонтальной плоскости запишем с учётом того, что силы, действующие на одинаковые вертикальные поверхности AD и CE, взаимно уравновешиваются. Остаётся только сила давления на площадь BE, которая пропорциональна вертикальной проекции S_в поверхности AB. С учётом частичного уравновешивания будем иметь условие равновесия сил в горизонтальном направлении в виде:

F_г=S_в•ρgh_c+Р₀S_в (2-11)

где h_с- глубина расположения центра тяжести поверхности AB.

Fx

Fx

D

FR

FR

δ

P

Зная F_г и F_в определим полную силуF, действующую на цилиндрическую поверхность

Рассмотрим трубу длиной l с внутренним диаметром D и толщиной стенок δ, находящуюся под действием гидростатического давления P. Это давление порождает разрывающие силы F_x. Из-за симметричности трубы такие разрывающие силы будут действовать одинаково во всех направлениях. Для вертикальной плоскости эта сила будет равна

F_х = πDl(2-12) ,

где произведение Dl – есть вертикальная проекция площади стенки трубы.

Рис.2.7. К определению разрывающей силы в трубе.

Разрывающей силе будут противодействовать силы реакции F_R, возникающие в стенках трубы. Площадь стенок трубы S_c в любом осевом сечении составит:

S_c=2l δ (2-13)

Под действием разрывающих сил в стенках трубы будет возникать суммарная сила реакция F_R, равная по величине разрывающей силе, но направленная в противоположную сторону:

F_R=F_X

Отсюда находится напряжение σ в стенках трубы, вызываемое давлением внутри трубы. Оно равняется

σ = F_R/S_c = (PDl)/ (2l δ) =PD/2 δ (2-14)

Закон Архимеда. Условие плавания тел.

Из рис.1.20 следует, что давление на нижнюю поверхность тела, погружённого в жидкость, больше, чем на верхнюю. Следовательно, и сила давления F₂>F_1. Пусть верхняя и нижняя грани куба, погружённого в жидкость, имеют площадь S. Объём такого тела будет равен V = (Н₂ - Н₁) S.

Рис. 2.8. Схема к определению силы Архимеда.

Разность сил давления на нижнюю и верхнюю грани куба:

F₂ - F₁ = (ρ g Н₂- ρ g Н₁)·S=ρ g( Н₂ - Н₁ ) S= ρ gV= m_жg = F_a(2-15)

называют выталкивающей силой или силой Архимеда. Она равна весу жидкости m_жg в объёме тела (вытесняемой телом). Если тело частично погружено в жидкость, то для расчёта силы Архимеда необходимо брать только объём погруженной части тела.

Если выталкивающая сила равна весу тела, тело плавает. Если же вес тела больше выталкивающей силы, тело тонет.

Примечание: вес тела можно найти по той же формуле, что и выталкивающую силу:

вес тела М= m_тg =ρ_тgV_т; F_a = m_жg = ρ_жgV_ж.(2-16)

Из формул 2-15 и 2-16 следует, что если плотность тела больше плотности жидкостиρ_т>ρ_ж , то тело плавает только в том случае, если объём вытесненной им жидкости больше объёма тела V_ж>V_т не менее чем в (ρ_т /ρ_ж ) раз. Поэтому лодкам и кораблям придают специальную форму, когда их собственный объём (дерева, металла) значительно меньше объёма воды, вытесняемой ими.

В Приложении 1 приведены сведения о приборах для измерения давления и о простейших гидравлических машинах. Этот дополнительный учебный материал следует изучить самостоятельно