Скорости и ускорения точек твердого тела, вращающегося вокруг неподвижной оси.
Рассмотрим движение твердого тела, при котором две точки его остаются неподвижными; такое движение представляет вращение тела вокруг проходящей через неподвижные точки прямой, называемой осью вращения. Пусть ось вращения тела совпадает с осью Oz. Чтобы определить положение тела, проведем через ось Oz две полуплоскости: подвижную Q, твердо связанную с вращающимся телом, и неподвижную Р (рис. 25). Заданием двугранного угла φ(t) между этими полуплоскостями положение твердого тела вполне определяется.  Траекторией любой точки М твердого тела, вращающегося вокруг неподвижной оси, является окружность (рис. 25), расположенная в плоскости, проведенной через М перпендикулярно к оси вращения; центр этой окружности находится в пересечении только что упомянутой плоскости и оси вращения; радиус окружности равен расстоянию h точки М от оси вращения. Дуга S(t), отсчитанная от начального положения Мо точки до положения ее М в момент t, соответствующая углу поворота φ, равна S(t)=hφ(t). Направляя, как всегда, касательную к траектории точки, в данном случае окружности, в сторону возрастания дуги, определим скорость в проекции ее на касательную:
Траекторией любой точки М твердого тела, вращающегося вокруг неподвижной оси, является окружность (рис. 25), расположенная в плоскости, проведенной через М перпендикулярно к оси вращения; центр этой окружности находится в пересечении только что упомянутой плоскости и оси вращения; радиус окружности равен расстоянию h точки М от оси вращения. Дуга S(t), отсчитанная от начального положения Мо точки до положения ее М в момент t, соответствующая углу поворота φ, равна S(t)=hφ(t). Направляя, как всегда, касательную к траектории точки, в данном случае окружности, в сторону возрастания дуги, определим скорость в проекции ее на касательную:
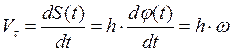 (28)
(28)
величина h вынесена за знак производной по времени как расстояние точки до оси, не изменяющееся при вращении твердого тела. Величину ω назовём угловой скоростью вращения тела. Скорость любой точки тела, вращающегося вокруг неподвижной оси, равна произведению угловой скорости тела на расстояние точки до оси вращения. Направление вектора скорости 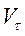 определится касательной к окружности, по которой движется точка. Таким образом, можно установить следующий закон распределения скоростей в теле, вращающемся вокруг неподвижной оси: в данный момент времени скорости различных точек тела пропорциональны их расстояниям от оси вращения и направлены в сторону вращения тела перпендикулярно к плоскостям, проходящим через ось вращения и рассматриваемые точки.
определится касательной к окружности, по которой движется точка. Таким образом, можно установить следующий закон распределения скоростей в теле, вращающемся вокруг неподвижной оси: в данный момент времени скорости различных точек тела пропорциональны их расстояниям от оси вращения и направлены в сторону вращения тела перпендикулярно к плоскостям, проходящим через ось вращения и рассматриваемые точки.
При вычислении линейных скоростей точек вращающегося тела по формуле (28) необходимо помнить, что угловая скорость должна быть выражена в рад/сек, (1/сек). Перейдем к рассмотрению ускорений точек тела, вращающегося вокруг неподвижной оси. Воспользуемся для этого формулами проекций ускорения на касательную и главную нормаль к траектории - и данном случае окружности радиуса h:
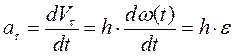 ,
, 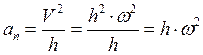 (2.9)
(2.9)
 здесь обозначено
здесь обозначено 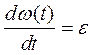 , где через ε обозначено угловое ускорение. Касательную и нормальную составляющие ускорения принято называть соответственно вращательной и осестремительной составляющими ускорения, или кратко вращательным и осестремительным ускорениями.
, где через ε обозначено угловое ускорение. Касательную и нормальную составляющие ускорения принято называть соответственно вращательной и осестремительной составляющими ускорения, или кратко вращательным и осестремительным ускорениями.
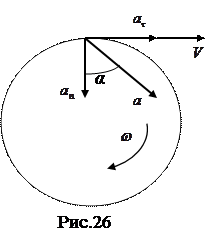
Осестремительная проекция ускорения, как видно из последней формулы, всегда положительна, т.е. осестремительное ускорение всегда направлено по радиусу окружности от точки к оси вращения. Что же касается вращательной составляющей, то она направлена по касательной в сторону положительного отсчета углов (и дуг), если ε > 0, и в противоположную сторону при ε < 0. На рис. 26 показано взаимное расположение вращательного и центростремительного ускорений и скорости при одном и том же направлении вращения тела. Полное ускорение точки вращающегося тела
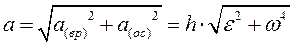 ,
,
угол α, образованный вектором ускорения 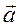 (рис. 26) с направлением нормали к траектории:
(рис. 26) с направлением нормали к траектории: 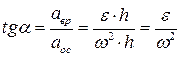 .
.
Таким образом, приходим к следующему закону распределения ускорений в твердом теле, вращающемся вокруг неподвижной оси: в данный момент времени ускорения точек тела пропорциональны расстояниям точек от оси вращения и наклонены под одинаковыми углами к радиусам вращения.
Рассмотрим пример. Сравним скорости и ускорения на ободе маховика паровой машины, имеющего диаметр D=l,5м и вращающегося с угловой скоростью N =240 об/мин, и турбинного диска, имеющего диаметр 10 см и совершающего 18 000 об/мин.
В первом случае 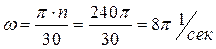 , h=D/2=0.75ми, следовательно, V=0,75•8π=18,85м/сек
, h=D/2=0.75ми, следовательно, V=0,75•8π=18,85м/сек 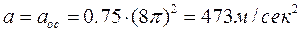 . Окружная скорость и центростремительное ускорение точки обода турбинного диска будут:
. Окружная скорость и центростремительное ускорение точки обода турбинного диска будут:
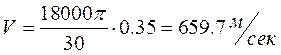 ,
, 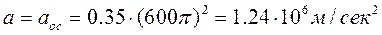
Ускорение частицы на ободе диска в 126000 раз превосходит ускорение силы тяжести g=9,81  .
.
