Гомогенный реактор с линейной температурной обратной связью
Рассмотрим точечную модель гомогенного реактора в предположении, что реактивность зависит от температуры горючего по линейному закону. Уравнения динамики запишутся в виде:
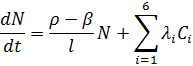
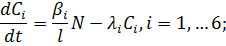
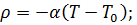 (4.1)
(4.1)
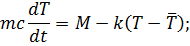
где N-мощность реактора; T-температура делящегося вещества; 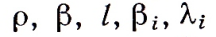 -постоянные ;
-постоянные ; 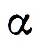 -температурный коэффициент реактивности; m и c-масса и удельная теплоемкость горючего. Постоянные k и
-температурный коэффициент реактивности; m и c-масса и удельная теплоемкость горючего. Постоянные k и 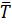 имеют различное содержание в зависимости от конкретного механизма отвода тепла. Так, если теплоотвод осуществляется циркуляцией горючего, то k=Gc, где G- массовый расход горючего, а
имеют различное содержание в зависимости от конкретного механизма отвода тепла. Так, если теплоотвод осуществляется циркуляцией горючего, то k=Gc, где G- массовый расход горючего, а 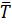 -постоянная температура горючего на входе в активную зону. Если же тепло отводится охлаждением через поверхность, то k- коэффициент теплопередачи от горючего с температурой Т к охлаждающей среде с температурой
-постоянная температура горючего на входе в активную зону. Если же тепло отводится охлаждением через поверхность, то k- коэффициент теплопередачи от горючего с температурой Т к охлаждающей среде с температурой 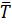 . В системе (4.1) и всюду ниже индекс «0» указывает на значение переменной в стационарной системе.
. В системе (4.1) и всюду ниже индекс «0» указывает на значение переменной в стационарной системе.
Система (4.1) допускает два разных состояния равновесия:

Первое состояние равновесия характеризует погашеный реактор. Второе состояние равновесия описывает стационарный режим при отличном от нуля уровне мощности.
Рассмотрим задачу устойчивости системы (4.1) в отклонениях при
ρ=ρ(t)=-α(Τ(t)-Τ0); Ν=Ν0(t); Ci=Ci0(t); Τ=Τ0(t); (4.2)
Перейдем к новым переменным
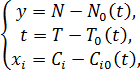
Учитывая уравнения (4.2) получим
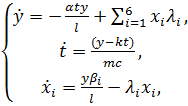 (4.3)
(4.3)
Применим функцию Ляпунова
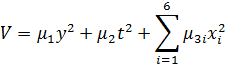
Производная от функции Ляпунова равна
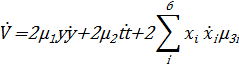
Подставляя соответствующие значения получим
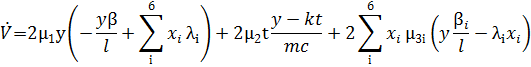
Раскрыв скобки получаем
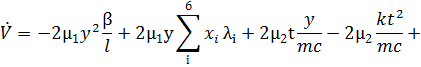
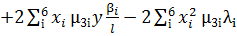 (4.4)
(4.4)
Выпишем матрицу коэффициентов квадратичной формы (4.4)
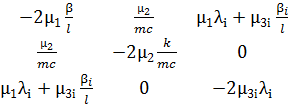
Применяя критерии асимптотической устойчивости линейного приближения, получим
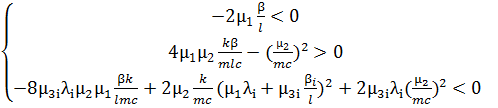 (4.5)
(4.5)
При условиях (4.5) система уравнений (4.3) асимптотически устойчива, а значит и исходная система (4.1) тоже асимптотически устойчива.
Было проведено численное моделирование системы (4.1) при следующих численных значениях (Приложение 1).
A=0.11;h1=0.07;h2=0.08;h3=0.04;h4=0.045;h5=0.05;h6=0.06;B=1;B1=0.01;B2=0.01;B3=0.01;B4=0.01;B5=0.01;B6=0.01;l=1;k=1;
m=1;c=1;
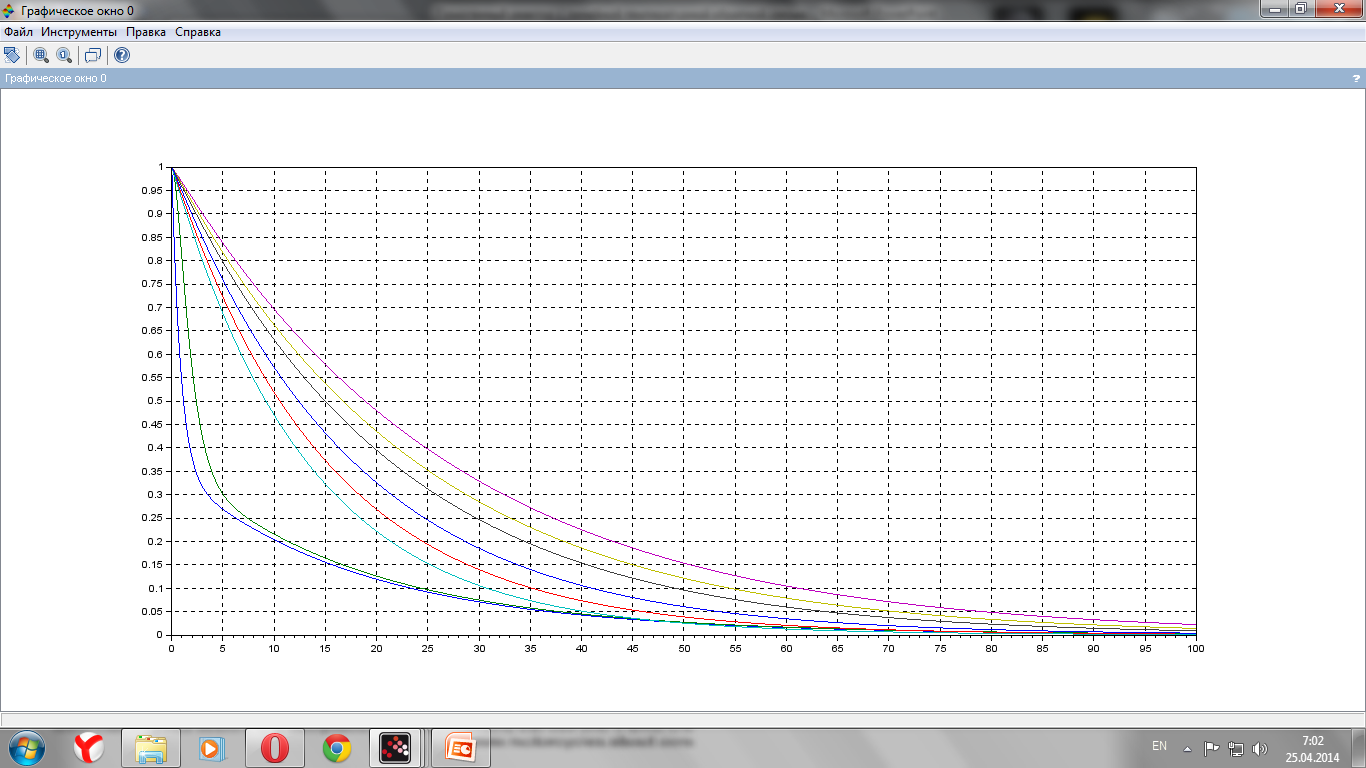
Рис 4.1.
Из рис. 4.1 можно сделать вывод, что система (4.1) является асимптотически устойчива при данных значений параметров.
Заключение.
В курсовой работе исследована задача устойчивости гомогенного реактора с линейной температурной обратной связью. С помощью теоремы об асимптотической устойчивости линейного приближения было доказано, что стационарный режим гомогенного реактора асимптотически устойчив. Основные численные результаты, полученные в данной работе, заключается в следующем:
- Составлена программа в системе scilab для численного интегрирования системы дифференциальных уравнений, описывающих уравнения динамики.
- Численное интегрирование подтвердило аналитические результаты об асимптотической устойчивости.
Литература.
1. Горяченко В.Д. Методы исследования устойчивости ядерных реакторов. М., Атомиздат , 1977. 296 с.
2. Пинни Э., Обыкновенные дифференциально-разностные уравнения, пер. с англ., М., 1961; Беллман Р., Кук К., Дифференциально-разностные уравнения, пер. с англ., М., 1967.
3. Мышкис А. Д., Эльсгольц Л. Э., Состояние и проблемы теории дифференциальных уравнений с отклоняющимся аргументом, "Успехи математических наук", 1967, т. 22, в. 2 (134) (библ.).
4. Эльсгольц Л. Э., Норкин С. Б., Введение в теорию дифференциальных уравнений с отклоняющимся аргументом, 2 изд., М., 1971.
5. М. А. Айзерман. Классическая механика. — Издание 2-е, переработанное. — М.: Наука, 1980. — 367 с.
6. А.А.КИРСАНОВ ВВЕДЕНИЕ В АНАЛИТИЧЕСКУЮ ДИНАМИКУ Псков : ПГПИ, 1999. - 304 c.
Приложение 1.Программа позволяющая проинтегрировать полученные дифференциальные уравнения.
A=0.11;h1=0.07;h2=0.08;h3=0.04;h4=0.045;h5=0.05;h6=0.06;B=1;B1=0.01;B2=0.01;B3=0.01;B4=0.01;B5=0.01;B6=0.01;l=1;k=1;
m=1;c=1;
function dx=fun(t, x)
dx(1)=A*x(2)*x(1)/l+x(3)*h1+x(4)*h2+x(5)*h3+x(6)*h4+x(7)*h5+
+x(8)*h6-B*x(1)/l;
dx(2)=(x(1)-k*x(2))/m/c;
dx(3)=x(1)*B1/l-h1*x(3);
dx(4)=x(1)*B2/l-h2*x(4);
dx(5)=x(1)*B3/l-h3*x(5);
dx(6)=x(1)*B4/l-h4*x(6);
dx(7)=x(1)*B5/l-h5*x(7);
dx(8)=x(1)*B6/l-h6*x(8);
Endfunction
t0=0; x0=[1;1;1;1;1;1;1;1]; T=0:0.1:100; x=ode(x0,t0,T,fun) ;
plot(T,x(1,:),T,x(2,:),T,x(3,:),T,x(4,:),T,x(5,:),T,x(6,:),T,x(7,:),T,x(8,:)); xgrid();
