Обобщенная симметричная задача собственных значений

Лекция 13

Обобщенная проблема и процедура Релея Ритца

Обобщенная симметричная задача собственных значений

В рассмотренных выше примерах механическая система специально подбиралась таким образом, что матрица масс системы была диагональной. В этом случае (см. лекцию 10) уравнения колебаний (уравнения Лагранжа 2-го рода) приводятся к задаче

(15.1)

с симметричной матрицей .

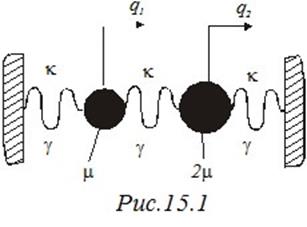
Однако рассмотрим следующий пример (рис. 15.1), отличающийся от примера из 10-й лекции лишь тем, что:

1) второй груз тяжелее первого в два раза;

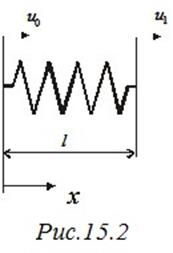
2) пружины не считаются невесомыми, но имеют массу .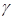

В этом случае вновь потенциальная энергия системы складывается из потенциальных энергий деформации пружин:

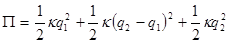. (15.2)

Что касается кинетической энергии системы, то сначала получим выражение для кинетической энергии отдельной пружины (рис. 15.2). Продольные перемещения в продольном направлении изменяются по линейному закону:

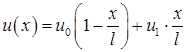(15.3)

Тогда, обозначив 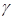массу пружины, получим для кинетической энергии пружины следующее выражение:

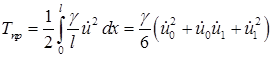. (15.4)

Теперь, имея формулу (15.4), мы можем без труда записать выражение для кинетической энергии всей системы (рис. 15.1), которая складывается из кинетических энергий двух грузов и трех пружин:

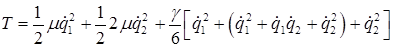. (15.5)

Вновь, как в лекции 10, воспользуемся уравнениями Лагранжа 2-го рода:

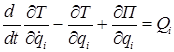. (15.6)

После вычисления производных кинетической и потенциальной энергий (15.5), (15.2) и подстановки их в (15.6) получим уравнения колебаний системы:

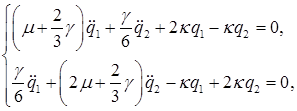(15.7)

или в матричном виде

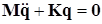, (15.8)

где

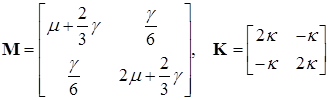. (15.9)

Теперь стандартная подстановка 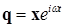приводит (15.7) к виду

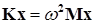. (15.10)

Казалось бы, умножив (15.10) на 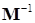, это уравнение можно привести к виду (15.1):

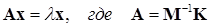. (15.11)

Однако хотя и матрица жесткости 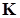, и матрица инерции 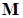симметричны, матрица 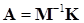оказывается симметричной лишь в частных случаях. Таких, например, как приведенные в лекции 10 где матрица 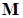была диагональной. Для рассмотренной выше задачи, которая совсем ненамного сложней, получим, положив для определенности ,

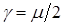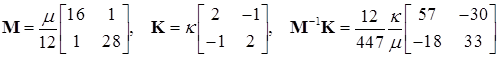. (15.12)

Что же это получается? Почти все рассмотренные методы были предназначены для симметричных матриц. И вот оказывается, что в большинстве случаев, представляющих практический интерес, эти методы неприменимы.

Конечно это не так, иначе мы не стали бы тратить столько времени на их изучение. Задача

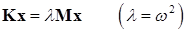(15.13)

в случае симметричных матриц 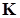и 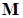сводится к задаче

(15.14)

с симметричной матрицей следующим образом.

Сначала выполним разложение матрицы 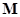по схеме Холецкого:

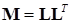. (15.15)

Это разложение возможно, так как матрица масс механической системы по физическому смыслу является положительно определенной. Подставляя (15.15) в (15.13) и вводя обозначение

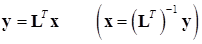, (15.16)

приводим систему (15.13) к виду

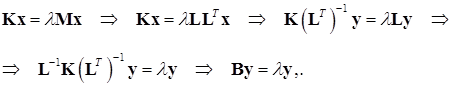(15.17)

где .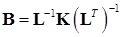

Матрица симметрична, так как

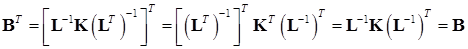. (15.18)

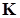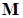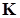Подводим итог. Собственные значения так называемой обобщенной задачи на собственные значения (15.13) при симметричных матрицах и совпадают с собственными значениями симметричной задачи (15.14), где матрица определяется через и 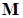(15.17). При этом собственные вектора обобщенной задачи 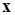выражаются через собственные вектора симметричной задачи соотношением (15.16).

Заключительное замечание. В преобразовании (15.17) используется матрица, обратная к треугольной 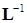. Сложно ли получить матрицу обратную данной? Нет, не сложно, и особенно для треугольной матрицы. В самом деле, если ввести обозначение 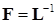, то, согласно определению обратной матрицы,

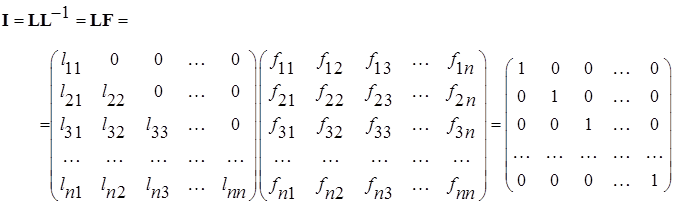(15.19)

Из определения матричного произведения следует, что (15.19) можно рассматривать как 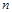линейных систем вида:

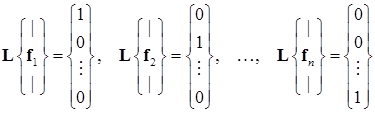, (15.20)

где 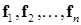– столбцы матрицы .

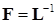Поскольку матрица 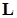- треугольная, системы (15.20) решаются очень легко. Кстати, с точки зрения эффективности алгоритма нет необходимости решать одну за другой систем (15.20). Гораздо меньше времени потребуется, если рассматривать (15.20) как одну систему, но с правыми частями.

Между прочим, в предыдущем замечании был почти полностью описан алгоритм вычисления обратной матрица, известный как метод Гаусса ‑ Жордана[1]. Для обращения произвольной невырожденной матрицы по этому методу следует сначала сформировать матрицу размера 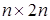и занести в первые столбцов матрицу , а в оставшиеся столбцов – единичную матрицу порядка :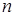

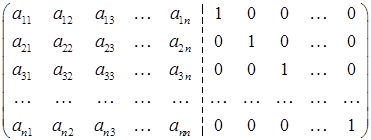. (15.21)

Далее к матрице применяется метод Гаусса. При этом сам процесс исключения выполняется только один раз, а операции с правыми частями повторяются для каждого столбца правой половины матрицы (15.21). Решение системы для каждого варианта правых частей заносится на место соответствующего столбца ‑ вектора правой части. Тогда по окончании процедуры Гаусса правые 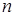столбцов (15.21) будут содержать решений системы вида:

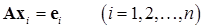, (15.22)

где через 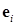обозначен 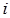-й столбец единичной матрицы.

Очевидно, что эти 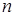столбцов и будут содержать матрицу обратную , так как согласно (15.22)

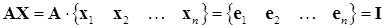. (15.23)