Определение уравнение переходных процессов в операторной форме

Расчет вторичных технических данных асинхронного двигателя

Таблица 1 – Исходные данные

Мощность Рд, кВт	n, об/мин	Динамический канал
160 кВт	3000	возмущение

Технические характеристики электродвигателя 5АМ315S2 приведены в таблице 2.

Таблица 2 – Технические характеристики электродвигателя RА250M4

P, кВт	nc, об/мин	ŋ, %	n2ном, об/мин	cos φ		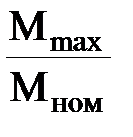		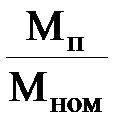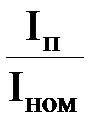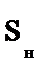,%	Jдв кг·м2
160	3000	94	2970	0,93	2,5	1,7	7,	2	0,44

Для асинхронного двигателя модуль жесткости механической характеристики рабочего участка 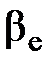( 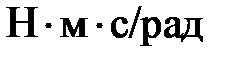) определяется по формуле:

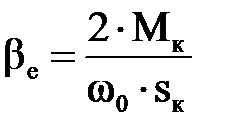, (1)

где 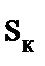– критическое скольжение, определяемое по формуле:

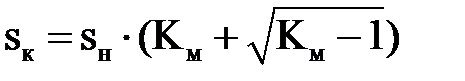, (2)

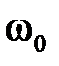– синхронная скорость вращения двигателя, определяемая по формуле

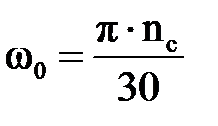, (3)

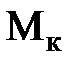- максимальный (критический момент) на валу двигателя, определяемый по формуле

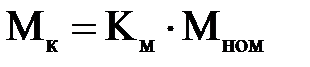, (4)

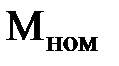- номинальный момент вращения, определяемый

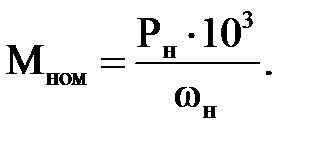(5)

где ω_н – номинальная угловая частота вращения вала двигателя, рад./с.

Номинальная угловая частота вращения вала двигателя ω_н (рад./с), определим по формуле:

ω_н = ω₀ · (1 – s_н). (6)

Определение уравнение переходных процессов в операторной форме

Структурная схема, характеризующая динамические свойства электропривода по каналу возмущения, представлена на рисунке 1.

Структурная схема состоит из следующих звеньев:

- регулятор момента W_рм (предназначен для поддержания заданного значения момента);

- электрический преобразователь W_п (предназначен для плавного регулирования потока электрической энергии, поступающей к двигателю);

- электромеханический преобразователь W_э (предназначен для преобразования электрической энергии в механическую);

- звено обратной связи К_ом (предназначено для согласования по уровню скорости вращения и сигнала задания скорости).

Рисунок 1 – Структурная схема электропривода.

Уравнение переходных процессов в общем виде записывается так:

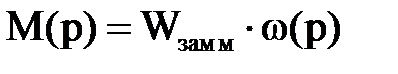, (2.1)

где М(р) – функция момента в операторной форме;

W_{зам м} – передаточная функция системы;

ω(р) – уравнение скорости вращения, в операторной форме, имеет вид:

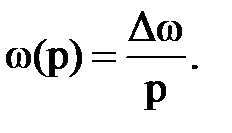(2.2)

Значение 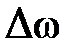задается в пределах не более 10 – 20 % от номинального значения скорости вращения. Принимаем

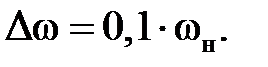(2.3)

Рисунок 2 – Структурная схема, характеризующая динамические свойства электропривода по каналу возмущения

Передаточная функция системы по каналу возмущения в операторной форме W^в_{зам м} определим по формуле:

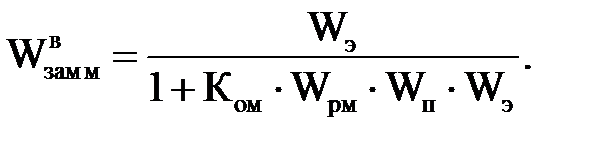(2.4)

Для одномассовой модели системы электропривода передаточная функция электрической части W_э определяется:

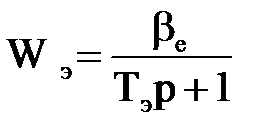, (2.5)

где 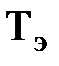- электромагнитная постоянная времени;

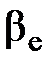- модуль жесткости механической характеристики рабочего участка, .

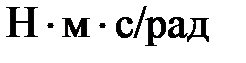Электромагнитная постоянная времени 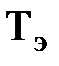определяется по формуле:

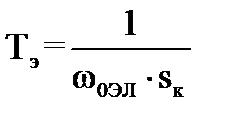, (2.6)

где 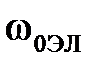- частота сети,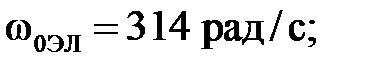

Для асинхронного двигателя модуль жесткости механической характеристики рабочего участка 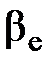( 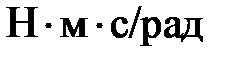) определяется по формуле:

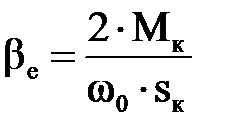, (2.7)

где 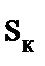– критическое скольжение, определяемое по формуле:

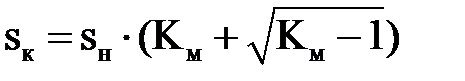, (2.8)

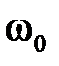– синхронная скорость вращения двигателя, определяемая по формуле

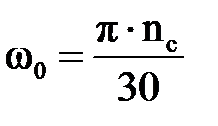, (2.9)

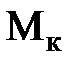- максимальный (критический момент) на валу двигателя, определяемый по формуле

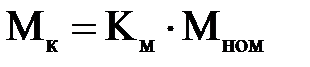, (2.10)

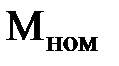- номинальный момент вращения, определяемый

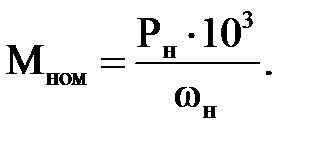(2.11)

где ω_н – номинальная угловая частота вращения вала двигателя, рад./с.

Номинальная угловая частота вращения вала двигателя ω_н (рад./с), определим по формуле:

ω_н = ω₀ · (1 – s_н). (2.12)

Подставив числовые значения в формулы (3), (5) – (12), получим:

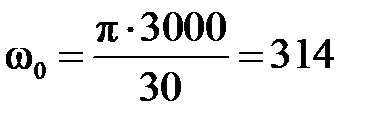рад./с;

ω_н = 314 · (1 – 0,02) = 307,72 рад./с;

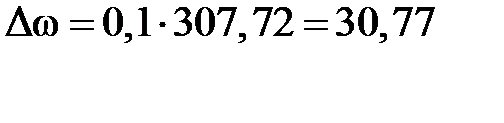рад./с;

;

.

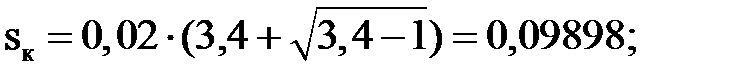
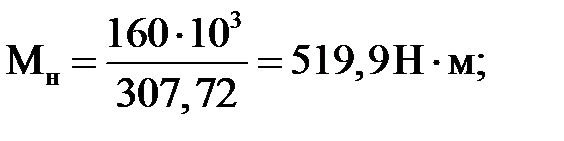
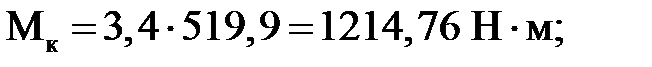
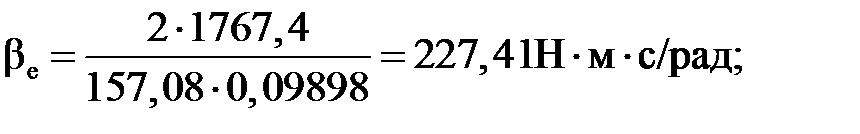
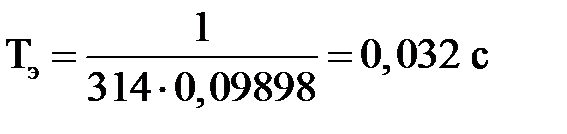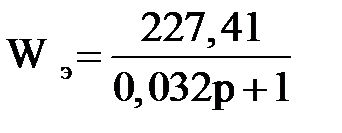Передаточная функция электрического преобразователя W_п определяется по формуле:

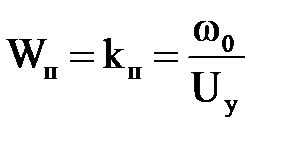, (2.13)

где U_у – управляющий сигнал, U_у = 16 мА.

.

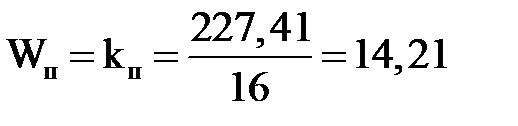Рассчитываем коэффициент обратной связи по моменту К_ом рассчитаем по формуле:

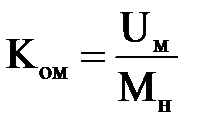, (2.14)

где U_м – сигнал пропорциональный моменту на валу двигателя, U_м = 16 мА.

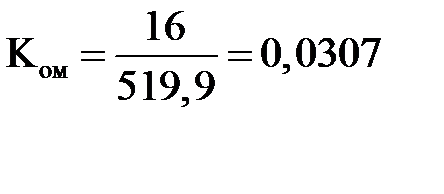
Передаточная функция регулятора момента W_рм определяется по формуле:

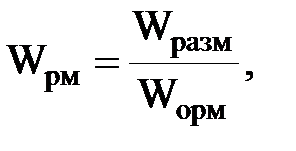(2.15)

где 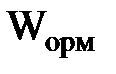- передаточная функция объекта регулирования момента;

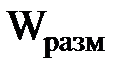- передаточная функция разомкнутой системы регулирования момента.

Передаточная функция объекта регулирования момента 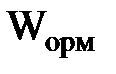, определим по формуле:

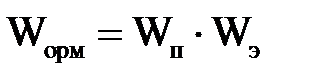; (2.16)

.

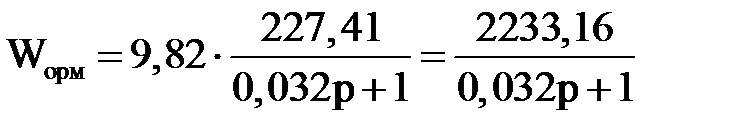Передаточная функция разомкнутой системы регулирования момента 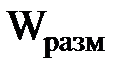определим по формуле:

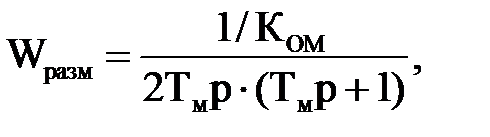(2.17)

где 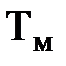- электромеханическая постоянная времени, .

;

.

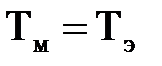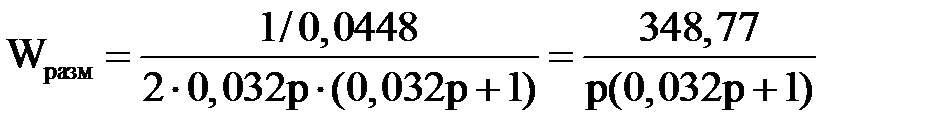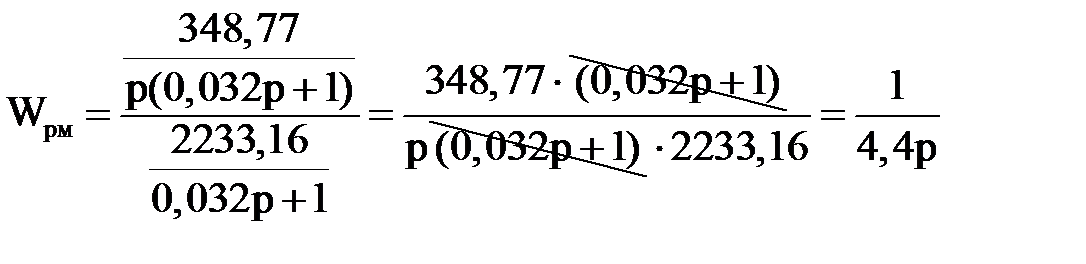И наконец, теперь, когда все множители уравнения (4) подсчитаны, подставим их в уравнение (4):

.

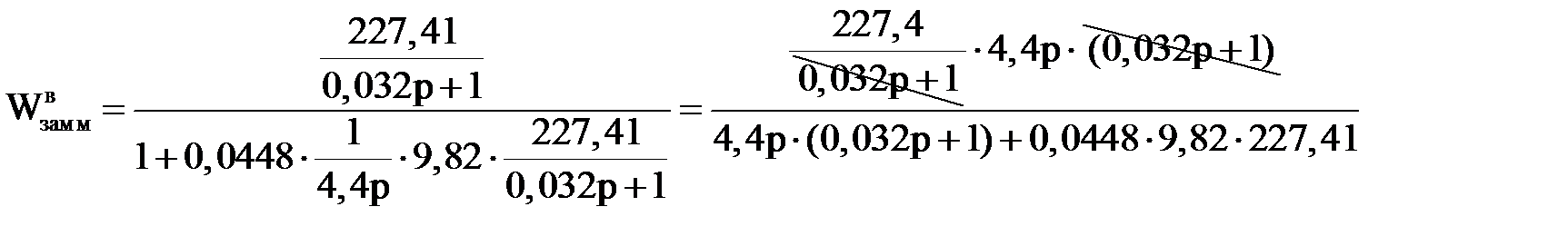
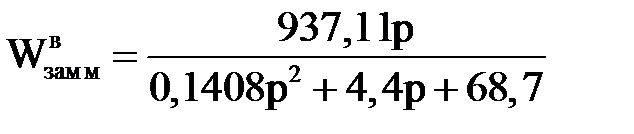Подставим результаты данных вычислений в формулу (1)

.
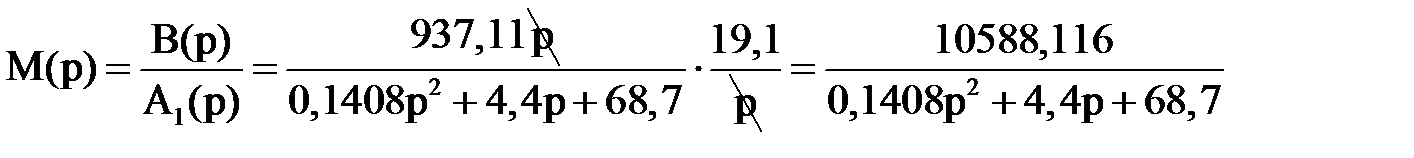